
Carico radiale come calcolarlo, esercizi risolti
Il carico radiale È la forza che viene esercitata perpendicolarmente all'asse di simmetria di un oggetto e la cui linea di azione passa per questo asse. Ad esempio, una cinghia su una puleggia impone un carico radiale sul cuscinetto o cuscinetto dell'albero della puleggia..
Nella figura 1 le frecce gialle rappresentano forze o carichi radiali sugli alberi dovuti alla tensione della cinghia che passa attraverso le pulegge.
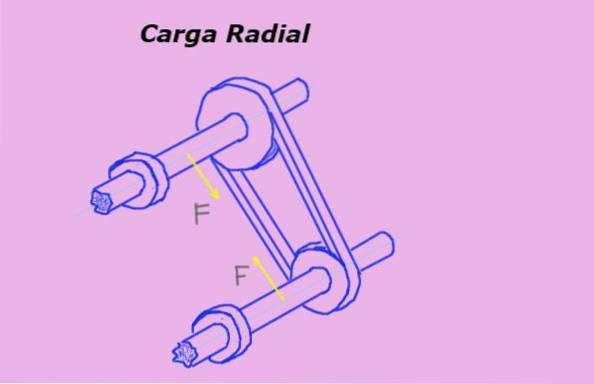
L'unità di misura del carico radiale nel sistema internazionale o SI è il Newton (N). Ma anche altre unità di forza sono spesso utilizzate per misurarlo, come il chilogrammo-forza (Kg-f) e la libbra-forza (lb-f).
Indice articolo
- 1 Come viene calcolato?
- 2 Esercizi risolti
- 2.1 -Esercizio 1
- 2.2 Esercizio 2
- 3 Riferimenti
Come viene calcolato?
Per calcolare il valore del carico radiale sugli elementi di una struttura, è necessario seguire i seguenti passaggi:
- Crea il diagramma delle forze su ogni elemento.
- Applicare le equazioni che garantiscono l'equilibrio traslazionale; cioè che la somma di tutte le forze è zero.
- Considera l'equazione delle coppie o dei momenti in modo che l'equilibrio rotazionale sia soddisfatto. In questo caso la somma di tutte le coppie deve essere zero.
- Calcola le forze per poter identificare i carichi radiali che agiscono su ciascuno degli elementi.
Esercizi risolti
-Esercizio 1
La figura seguente mostra una puleggia attraverso la quale passa una puleggia in tensione con tensione T. La puleggia è montata su un albero supportato da due cuscinetti. Il centro di uno di loro è a una distanza L1 dal centro della puleggia. All'altra estremità c'è l'altro rilevamento, alla distanza LDue.
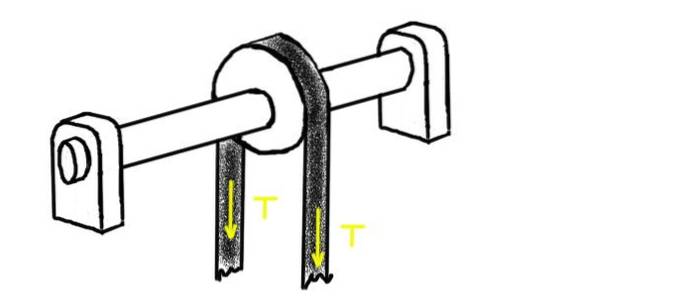
Determinare il carico radiale su ciascuno dei cuscinetti, assumendo che il peso dell'albero e della puleggia sia significativamente inferiore alla sollecitazione applicata.
Prendere come valore per la tensione della cinghia 100 kg-f e per le distanze L1= 1 me LDue= 2 m.
Soluzione
Innanzitutto, viene creato un diagramma delle forze che agiscono sull'asse.
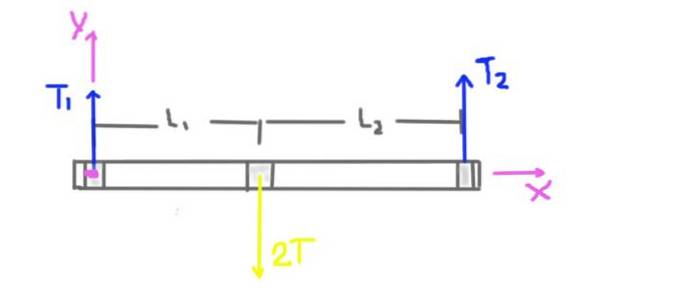
La tensione della puleggia è T, ma il carico radiale sull'albero nella posizione della puleggia è 2T. Il peso dell'albero e della puleggia non viene preso in considerazione perché l'enunciato del problema ci dice che è notevolmente inferiore alla tensione applicata alla cinghia.
La reazione radiale dei supporti sull'albero è causata dalle forze o carichi radiali T1 e T2. Nello schema sono indicate anche le distanze L1 e L2 dai supporti al centro della puleggia..
Viene visualizzato anche il sistema di coordinate. La coppia o il momento totale sull'asse verrà calcolato prendendo come centro l'origine del sistema di coordinate e sarà positivo in direzione Z.
Condizioni di equilibrio
Ora le condizioni di equilibrio sono stabilite: somma delle forze uguale a zero e somma delle coppie uguale a zero.
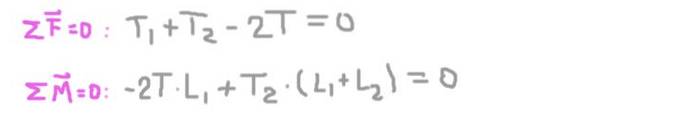
Dalla seconda equazione otteniamo la reazione radiale sull'asse nel supporto 2 (TDue), sostituendo nel primo e risolvendo la reazione radiale sull'asse al supporto 1 (T1).
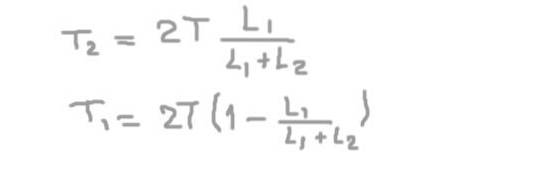
T1= (2/3) T = 66,6 kg-f
E il carico radiale sull'albero nella posizione del supporto 2 è:
TDue= (4/3) T = 133,3 kg-f.
Esercizio 2
La figura seguente mostra un sistema composto da tre pulegge A, B, C tutte dello stesso raggio R. Le pulegge sono collegate da una cinghia che ha una tensione T.
Gli alberi A, B, C passano attraverso cuscinetti lubrificati. La distanza tra i centri degli assi A e B è 4 volte il raggio R. Allo stesso modo, anche la separazione tra gli assi B e C è 4R.
Determinare il carico radiale sugli assi delle pulegge A e B, assumendo che la tensione della cinghia sia 600N.
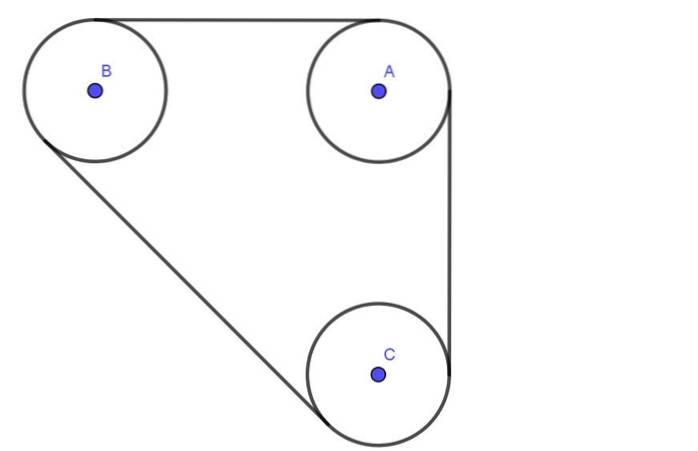
Soluzione
Iniziamo disegnando un diagramma delle forze che agiscono sulla puleggia A e su B. Sulla prima abbiamo le due tensioni T1 e TDue, così come la forza FPER che il cuscinetto esercita sull'asse A della puleggia.
Allo stesso modo, sulla puleggia B abbiamo le tensioni T3 , T4 e la forza FB che il cuscinetto esercita sull'asse dello stesso. Il carico radiale sull'asse della puleggia A è la forza FPER e il carico radiale su B è la forza FB.
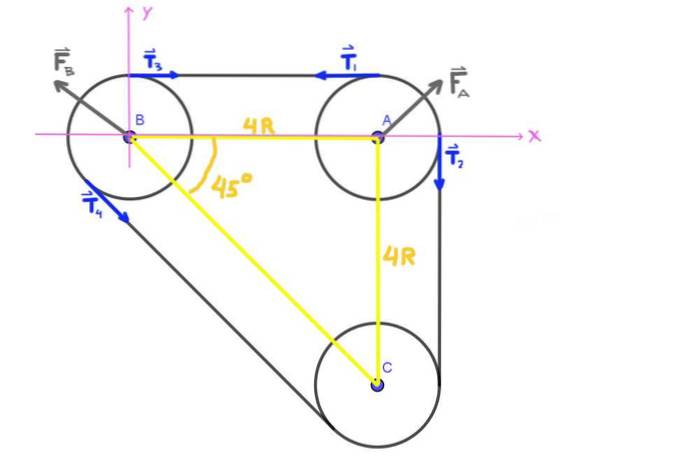
Poiché gli assi A, B, C formano un triangolo isorettangolo, l'angolo ABC è di 45 °.
Tutte le tensioni T1 , TDue , T3 , T4 mostrati in figura hanno lo stesso modulo T, che è la tensione della cinghia.
Condizione di equilibrio per la puleggia A
Scriviamo ora la condizione di equilibrio per la puleggia A che altro non è che la somma di tutte le forze agenti sulla puleggia A deve essere zero.
Separando le componenti X e Y delle forze e aggiungendo (vettorialmente) si ottiene la seguente coppia di equazioni scalari:
FPERX - T = 0; FPERY - T = 0
Queste equazioni portano alla seguente uguaglianza: FASCIA = FOH = T.
Pertanto il carico radiale ha grandezza data da:
FPER = (T² + T²)1/2 = 21/2∙ T = 1,41 ∙ T = 848,5 N. con direzione 45 °.
Condizione di equilibrio per la puleggia B
Allo stesso modo, scriviamo la condizione di equilibrio per la puleggia B. Per il componente X abbiamo: FBX + T + T ∙ Cos45 ° = 0
Y per componente Y: FBY + T ∙ Sen45 ° = 0
Quindi:
FBX = - T (1 + 2-1/2) e FDI = -T ∙ 2-1/2
Cioè, l'entità del carico radiale sulla puleggia B è:
FB = ((1 + 2-1/2) ² + 2-1)1/2∙ T = 1,85 ∙ T = 1108,66 N e la sua direzione è 135 °.
Riferimenti
- Beer F, Johnston E, DeWolf J, Mazurek, D.Meccanica dei materiali. Quinta edizione. 2010. Mc Graw Hill. 1-130.
- Gere J, Goodno, B. Meccanica dei materiali. Ottava edizione. Cengage Learning. 4-220.
- Giancoli, D. 2006. Fisica: principi con applicazioni. 6tth Ed. Prentice Hall. 238-242.
- Hibbeler R. Meccanica dei materiali. Ottava edizione. Prentice Hall. 2011. 3-60.
- Valera Negrete, J. 2005. Note sulla fisica generale. UNAM. 87-98.

Nessun utente ha ancora commentato questo articolo.