
Carico assiale come viene calcolato ed esercizi risolti
Il carico assiale È la forza diretta parallelamente all'asse di simmetria di un elemento che costituisce una struttura. La forza o il carico assiale può essere tensione o compressione. Se la linea di azione della forza assiale coincide con l'asse di simmetria che passa per il baricentro dell'elemento considerato allora si dice che sia un carico o forza assiale concentrico.
Al contrario, se è una forza assiale o un carico parallelo all'asse di simmetria, ma la cui linea di azione non è sull'asse stesso, è una forza assiale eccentrica.
-
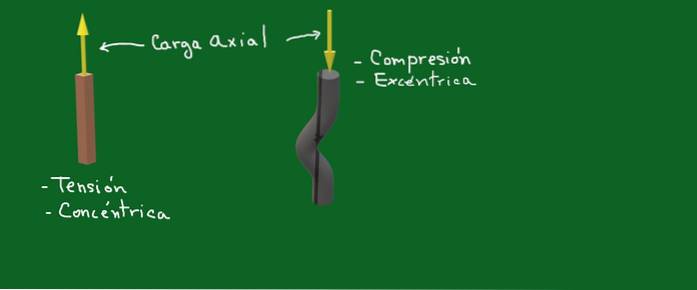
Figura 1. Carico assiale. Fonte: autocostruito
Nella figura 1 le frecce gialle rappresentano forze o carichi assiali. In un caso si tratta di una forza di tensione concentrica e nell'altro si tratta di una forza di compressione eccentrica.
L'unità di misura del carico assiale nel sistema internazionale SI è il Newton (N). Ma vengono spesso utilizzate anche altre unità di forza come chilogrammo-forza (kg-f) e libbra-forza (lb-f)..
Indice articolo
- 1 Come viene calcolato?
- 1.1 Rapporto tra carico assiale e sollecitazione normale
- 2 Esercizi risolti
- 2.1 -Esercizio 1
- 2.2 -Esercizio 2
- 3 Riferimenti
Come viene calcolato?
Per calcolare il valore del carico assiale negli elementi di una struttura, è necessario seguire i seguenti passaggi:
- Crea il diagramma delle forze su ogni elemento.
- Applicare le equazioni che garantiscono l'equilibrio traslazionale, ovvero che la somma di tutte le forze sia zero.
- Considera l'equazione delle coppie o dei momenti in modo che l'equilibrio rotazionale sia soddisfatto. In questo caso la somma di tutte le coppie deve essere zero.
- Calcola le forze e identifica le forze o i carichi assiali in ciascuno degli elementi.
Rapporto tra carico assiale e sollecitazione normale
Lo stress normale medio è definito come il rapporto del carico assiale diviso per l'area della sezione trasversale. Le unità di sforzo normale nel Sistema Internazionale S.I. sono Newton su metro quadrato (N / m²) o Pascal (Pa). La figura 2 seguente illustra il concetto di stress normale per chiarezza..
-
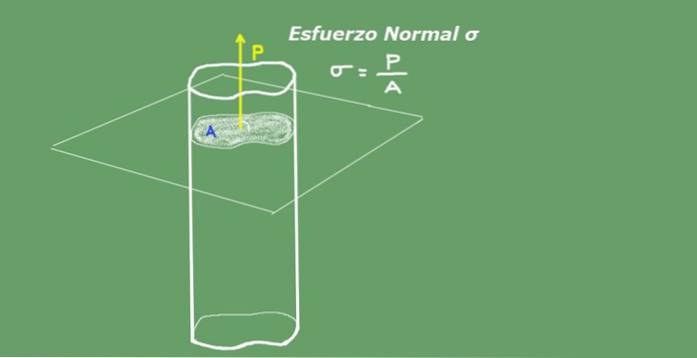
Figura 2. Stress normale. Fonte: autocostruito.
Esercizi risolti
-Esercizio 1
Si consideri una colonna cilindrica in cemento di altezza he raggio r. Supponiamo che la densità del calcestruzzo sia ρ. La colonna non supporta alcun carico aggiuntivo oltre al proprio peso ed è supportata su una base rettangolare.
- Trovare il valore del carico assiale nei punti A, B, C e D, che sono nelle seguenti posizioni: A alla base della colonna, B a ⅓ di altezza h, C a ⅔ di altezza he per ultimo D a la parte superiore della colonna.
- Determina anche lo stress normale medio in ciascuna di queste posizioni. Prendi i seguenti valori numerici: h = 3m, r = 20cm e ρ = 2250 kg / m³
-
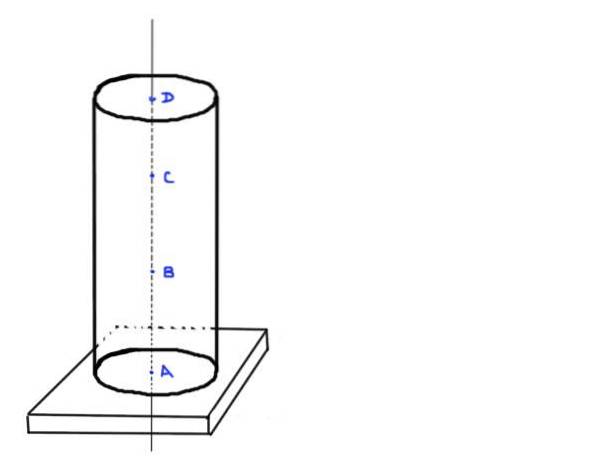
Figura 3. Colonna cilindrica. Fonte: autocostruito.
Soluzione
Peso totale della colonna
Il peso totale W della colonna è il prodotto della sua densità per il volume moltiplicato per l'accelerazione di gravità:
W = ρ ∙ h ∙ π ∙ r² ∙ g = 8313 N
Carico assiale in A
Nel punto A la colonna deve sostenere tutto il suo peso, quindi il carico assiale in questo punto di compressione è uguale al peso della colonna:
PA = W = 8313 N
Carico assiale in B
Solo ⅔ della colonna sarà sul punto B, quindi il carico assiale in quel punto sarà la compressione e il suo valore ⅔ il peso della colonna:
PB = ⅔ W = 5542 N
Figura 3. Colonna cilindrica. Fonte: autocostruito.
Sopra la posizione C c'è solo ⅓ della colonna, quindi il suo carico assiale in compressione sarà ⅓ del suo stesso peso:
PC = ⅓ W = 2771 N
Carico assiale in D
Infine, non c'è carico sul punto D, che è l'estremità superiore della colonna, quindi la forza assiale in quel punto è zero..
PD = 0 N
Sforzi normali in ciascuna delle posizioni
Per determinare la sollecitazione normale in ciascuna delle posizioni, sarà necessario calcolare la sezione trasversale dell'area A, che è data da:
A = π ∙ r² = 0,126m²
In questo modo, la sollecitazione normale in ciascuna delle posizioni sarà il quoziente tra la forza assiale in ciascuno dei punti diviso per l'area della sezione trasversale già calcolata, che in questo esercizio è la stessa per tutti i punti perché è una colonna cilindrica.
σ = P / A; σA = 66,15 kPa; σB = 44,10 kPa; σC = 22,05 kPa; σD = 0,00 kPa
-Esercizio 2
La figura mostra una struttura composta da due barre che chiameremo AB e CB. La barra AB è supportata all'estremità A da un pin e all'altra estremità collegata all'altra barra da un altro pin B.
Allo stesso modo, la barra CB è supportata all'estremità C tramite un perno e all'estremità B con il perno B che la collega all'altra barra. Una forza verticale o un carico F viene applicato al pin B come mostrato nella figura seguente:
-
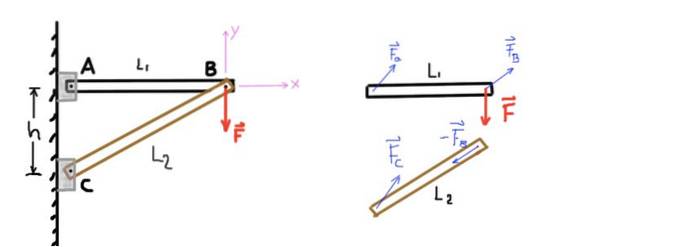
Figura 4. Struttura a due barre e diagramma a corpo libero. Fonte: autocostruito.
Supponiamo che il peso delle barre sia trascurabile, poiché la forza F = 500 kg-f è molto maggiore del peso della struttura. La distanza tra i supporti A e C è h = 1,5 me la lunghezza della barra AB è L1 = 2 m. Determina il carico assiale su ciascuna delle barre, indicando se si tratta di carico assiale in compressione o trazione.
Soluzione 2
La figura mostra, mediante un diagramma a corpo libero, le forze agenti su ciascuno degli elementi della struttura. Viene inoltre indicato il sistema di coordinate cartesiane con cui verranno stabilite le equazioni di equilibrio delle forze..
Coppie o momenti verranno calcolati nel punto B e saranno considerati positivi se puntano lontano dallo schermo (asse Z). L'equilibrio di forze e coppie per ogni barra è:
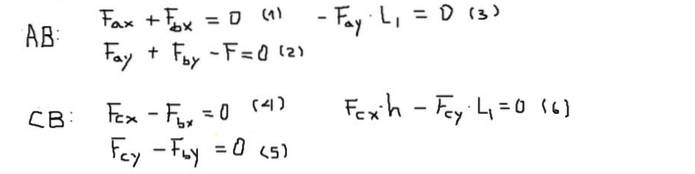
Successivamente, i componenti delle forze di ciascuna delle equazioni vengono risolti nel seguente ordine:
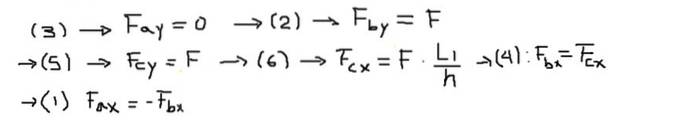
Infine, vengono calcolate le forze risultanti alle estremità di ciascuna barra:
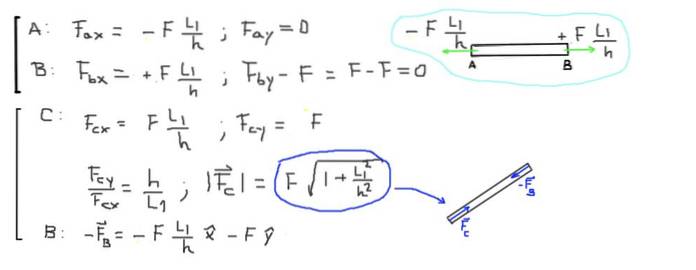
F ∙ (L1 / h) = 500 kg-f ∙ (2,0 m / 1,5 m) = 666,6 kg-f = 6533,3 N
La barra CB è in compressione a causa delle due forze agenti alle sue estremità parallele alla barra e rivolte verso il suo centro. L'entità della forza di compressione assiale nella barra CB è:
F ∙ (1 + L1² / h²) 1/2 = 500 kg-f ∙ (1 + (2 / 1.5) ²) 1/2 = 833,3 kg-f = 8166,6 N
Riferimenti
- Beer F… Meccanica dei materiali. 5 °. Edizione. 2010. Mc Graw Hill. 1-130.
- Hibbeler R. Meccanica dei materiali. Ottava edizione. Prentice Hall. 2011. 3-60.
- Gere J. Meccanica dei materiali. Ottava edizione. Cengage Learning. 4-220.
- Giancoli, D. 2006. Fisica: principi con applicazioni. 6a Ed. Prentice Hall. 238-242.
- Valera Negrete, J. 2005. Note sulla fisica generale. UNAM. 87-98.


Nessun utente ha ancora commentato questo articolo.