
Formule di accelerazione negativa, calcolo ed esercizi risolti
Il accelerazione negativa Si verifica quando il cambiamento o la variazione della velocità durante un periodo di tempo ha un segno negativo. Osserva il cane nell'immagine che si diverte sulla spiaggia. La sabbia rallenta il suo movimento, il che significa che c'è un'accelerazione opposta alla velocità che sta trasportando.
Questa accelerazione può essere considerata negativa, in contrapposizione alla velocità, che è dichiarata positiva. Sebbene un'accelerazione negativa non sempre causa una riduzione della velocità.

In un movimento unidimensionale, la direzione di avanzamento è generalmente considerata positiva, cioè la direzione della velocità. Questo è quanto si è considerato in precedenza: nel cane in figura la direzione positiva è quella che va dalla coda alla testa.
Prima di affondare le zampe nella sabbia, il cane è arrivato con una certa velocità v avanti, questo è positivo. Quindi la sabbia diminuisce la sua velocità fino a quando non si ferma, cioè a zero velocità finale.
Supponiamo che tutto questo sia accaduto in un periodo di tempo Δt. L'accelerazione durante questo tempo verrà calcolata in questo modo:
a = (0 - v) ÷ Δt
Nell'equazione precedente v> 0, Δt> 0 poi a < 0, es decir aceleración negativa (per < 0). Poiché la direzione della velocità all'inizio è stata presa come positiva, un'accelerazione negativa significa che l'accelerazione punta lontano dalla velocità. Pertanto si conclude che:
Ogni volta che l'accelerazione di un corpo in movimento punta nella direzione opposta alla velocità, il corpo sta frenando o decelerando.
Possiamo quindi stabilire che:
- Quando velocità e accelerazione hanno lo stesso segno, indipendentemente da quale segno, la velocità aumenta. In questo caso, la velocità diventa più positiva o più negativa, a seconda dei casi..
- Quando la velocità e l'accelerazione hanno segni opposti, la velocità diminuisce.
Indice articolo
- 1 Formule per il calcolo dell'accelerazione
- 1.1 -Esempio 1
- 1.2 -Esempio 2
- 1.3 -Esempio 3-Il lancio verticale
- 2 Riferimenti
Formule per il calcolo dell'accelerazione
Indipendentemente dal segno, l'accelerazione media perm tra i momenti t Y t ' viene calcolato utilizzando la seguente formula:
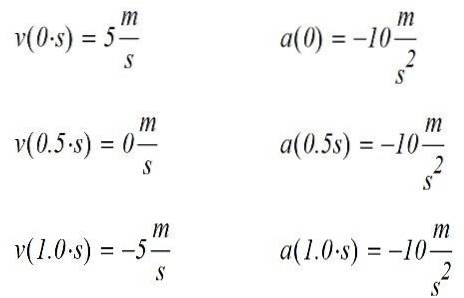
L'accelerazione media fornisce informazioni globali su come la velocità è cambiata nell'intervallo di tempo considerato. D'altra parte, l'accelerazione istantanea offre il dettaglio di come la velocità cambia in ogni momento. Quindi per un dato istante t, l'accelerazione è calcolata dalla seguente formula:
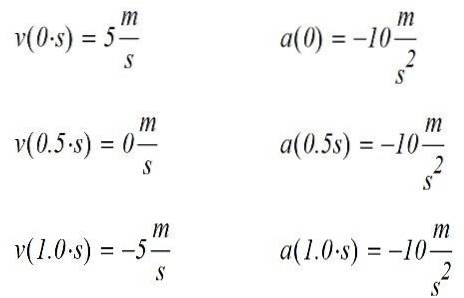
-Esempio 1
All'istante iniziale t = 0,2 s un oggetto ha una velocità di 3 m / s. Successivamente, all'istante t '= 0.4 s, ha una velocità di 1 m / s. Calcola l'accelerazione media tra i tempi t e t 'e interpreta il risultato.
Risposta
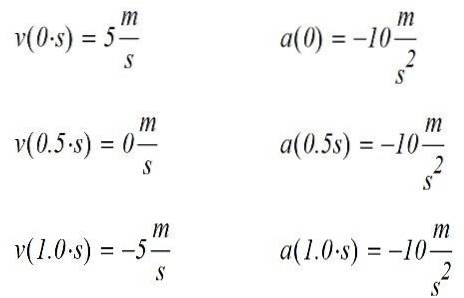
-Esempio 2
All'istante iniziale t = 0,6 s un oggetto ha velocità -1 m / s. Successivamente, all'istante t '= 0,8 s, ha una velocità di -3 m / s. Calcola l'accelerazione media tra i tempi t e t '. Interpreta il risultato.
Risposta
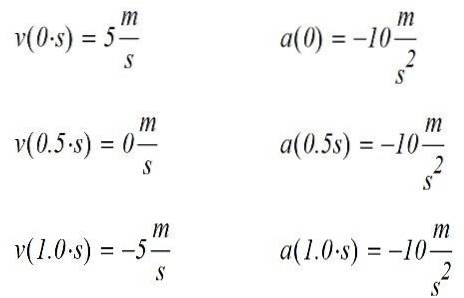
In conclusione, alla fine dell'intervallo di tempo la velocità è diventata ancora più negativa (-3m / s).
Questo significa che il cellulare rallenta il suo movimento? No. Il segno meno nella velocità significa solo che sta andando all'indietro e più veloce, poiché andando a -3 m / s sta andando più veloce di -1m / s, la velocità che era all'inizio.
La velocità, che è il modulo della velocità, è aumentata nonostante abbia un'accelerazione negativa. Voglio dire, questo oggetto ha accelerato. Quindi concludiamo:
Finché l'accelerazione di un corpo in movimento punta in una direzione parallela alla velocità, il corpo sta accelerando.
-Esempio 3-Il lancio verticale
Considera il seguente esempio: un oggetto ha velocità istantanea data dalla seguente espressione, con tutte le unità nel Sistema Internazionale:
v (t) = 5 - 10t
Trova la velocità e l'accelerazione per i tempi 0, 0,5 e 1,0. In ogni caso indicare se l'oggetto sta accelerando o decelerando.
Risposta
La velocità in ciascuno degli istanti indicati si trova sostituendo t direttamente nell'equazione. L'accelerazione si trova derivando l'espressione data in funzione del tempo e quindi valutando il risultato in ciascuno dei momenti dati.
I risultati sono i seguenti:
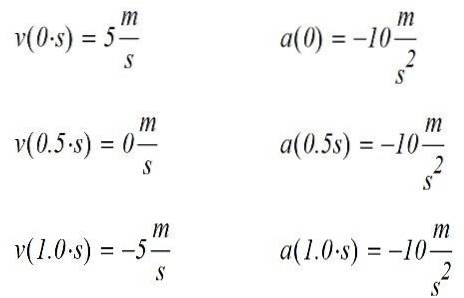
L'accelerazione è costante e negativa per tutti i movimenti. Ora è possibile descrivere cosa è successo al cellulare mentre si muove.
Al tempo t = 0 s il cellulare stava rallentando. Ciò segue immediatamente poiché la velocità è positiva e l'accelerazione è negativa..
Nell'istante t = 0,5 s il cellulare si è fermato, almeno momentaneamente era a riposo. Non è impossibile che un cellulare si fermi anche quando è accelerato. L'esempio più palpabile è nel vomito verticale.

Quando un mobile è proiettato verticalmente verso l'alto, riesce a raggiungere un'altezza massima. Se si sceglie la direzione positiva in quel senso, che è quasi sempre quello che si fa, durante il tempo necessario per raggiungere quel punto massimo, il mobile avrà velocità positiva.
Ma la gravità esiste da tutto il tempo. Ed è sempre diretto verticalmente verso il basso, indipendentemente dal fatto che l'oggetto stia salendo o scendendo. Naturalmente riesce a far rallentare gradualmente il cellulare fino a quando non si ferma per un istante.
Immediatamente il cellulare inverte il senso della sua velocità e torna a terra. In questo caso la velocità è negativa perché punta anche verso il suolo. Quindi la gravità fa sì che la velocità aumenti sempre di più.
Il valore dell'accelerazione di gravità è stato stimato in 9,8 m / sDue, che ai fini del calcolo viene arrotondato a 10 m / sDue. L'oggetto nell'esempio potrebbe essere stato lanciato verso l'alto con una velocità iniziale di 5 m / s..
Infine a t = 1.0 s, la velocità del cellulare è negativa. Se è un lancio verticale verso l'alto, in assenza di attrito, significa che sta attraversando nuovamente il punto di partenza, ma questa volta sta andando verso il basso, invece che verso l'alto..
In conclusione, un'accelerazione negativa non significa necessariamente che il cellulare stia rallentando. Al contrario, il cellulare potrebbe andare sempre più veloce. Si tratta di prestare attenzione al fatto che i segni di velocità e accelerazione siano gli stessi o meno..
Riferimenti
- Walker, J. 2010. Fisica. Quarta edizione. Addison Wesley. 26-30.


Nessun utente ha ancora commentato questo articolo.