Accelerazione media come viene calcolata ed esercizi risolti

Il accelerazione media per_m È la grandezza che descrive la variazione della velocità di una particella nel corso del tempo. È importante, perché mostra le variazioni che il movimento sperimenta.

Per esprimere questa grandezza in termini matematici, è necessario considerare due velocità e due istanti di tempo, che sono rispettivamente denotati come v₁ e V_Due, e tu₁ e tu_Due.

Combinando i valori secondo la definizione offerta, si otterrà la seguente espressione:

Nel sistema SI internazionale le unità per a_m sarà m / s^Due, sebbene altre unità che coinvolgono la lunghezza per unità di tempo al quadrato andranno bene.

Ad esempio, c'è il km / h.s che viene letto "chilometro all'ora e al secondo". Notare che l'unità di tempo appare due volte. Pensando a un cellulare che si muove lungo una linea retta, significa che per ogni secondo trascorso, il cellulare aumenta la sua velocità di 1 km / h. O lo diminuisce di 1 km / h per ogni secondo che passa.

Indice articolo

• 1 Accelerazione, velocità e velocità
• 2 Come viene calcolata l'accelerazione media
• 3 segni di accelerazione nel movimento unidimensionale
• 4 Caduta libera: un movimento con accelerazione costante
• 5 Esercizio risolto
  • 5.1 Risposta
• 6 Riferimenti

Accelerazione, velocità e velocità

Sebbene l'accelerazione sia associata ad un aumento della velocità, la verità è che osservando attentamente la definizione, si scopre che qualsiasi variazione di velocità implica l'esistenza di un'accelerazione.

E la velocità non cambia necessariamente sempre di grandezza. Può accadere che il cellulare cambi solo direzione e mantenga la sua velocità costante. C'è ancora un'accelerazione responsabile di questo cambiamento.

Un esempio di questo è un'auto che fa una curva con una velocità costante di 60 km / h. Il veicolo è soggetto ad accelerazione, che è responsabile del cambiamento della direzione della velocità in modo che l'auto segua la curva. Il conducente lo applica utilizzando il volante.

Tale accelerazione è diretta verso il centro del percorso curvo, per evitare che l'auto si allontani. Riceve il nome di accelerazione radiale o normale. Se l'accelerazione radiale venisse improvvisamente annullata, l'auto non sarebbe più in grado di continuare a girare in curva e continuerebbe in linea retta.

Un'auto che percorre una curva è un esempio di movimento in due dimensioni, mentre quando procede in linea retta, il suo movimento è unidimensionale. In questo caso, l'unico effetto dell'accelerazione è quello di modificare la velocità dell'auto..

Questa accelerazione è chiamata accelerazione tangenziale. Non è esclusivo del movimento unidimensionale. L'auto che percorre la curva a 60 km / h potrebbe contemporaneamente accelerare fino a 70 km / h mentre la percorre. In questo caso, il conducente deve utilizzare sia il volante che il pedale dell'acceleratore..

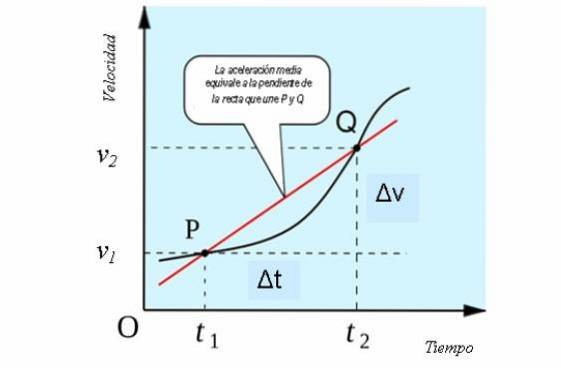
Se consideriamo un moto unidimensionale, l'accelerazione media ha un'interpretazione geometrica simile a quella della velocità media, come la pendenza della retta secante che interseca la curva nei punti P e Q del grafico velocità in funzione del tempo..

Questo può essere visto nella figura seguente:

Come viene calcolata l'accelerazione media

Vediamo alcuni esempi per calcolare l'accelerazione media in varie situazioni:

I) Ad un certo istante, un mobile che si muove lungo una linea retta ha una velocità di + 25 km / he 120 secondi dopo ne ha un'altra di -10 km / h. Qual è stata l'accelerazione media?

Risposta

Poiché il movimento è unidimensionale, si può fare a meno della notazione vettoriale, nel qual caso:

v_o = +25 km / h = +6,94 m / s

v_F = -10 km / h = - 2,78 m / s

Δt = 120 s

Ogni volta che hai un esercizio con grandezze miste come questo, in cui ci sono ore e secondi, è necessario trasferire tutti i valori alle stesse unità.

Essendo un movimento unidimensionale, la notazione vettoriale è stata eliminata.

II) Un ciclista viaggia verso est a una velocità di 2,6 m / se 5 minuti dopo va a sud a 1,8 m / s. Trova la sua accelerazione media.

Risposta

Il movimento non è unidimensionale, quindi viene utilizzata la notazione vettoriale. I vettori unitari io Y j indicare le direzioni insieme alla seguente convenzione di segno, facilitando il calcolo:

• Nord: +j
• Sud: -j
• Est: +io
• Ovest: -io

v_Due = - 1,8 j SM

v₁ = + 2,6 io SM

Δt = 5 minuti = 300 secondi

Segni di accelerazione nel movimento unidimensionale

Come sempre con le grandezze medie o medie, le informazioni fornite sono globali. Non offrono dettagli su ciò che è accaduto al cellulare in ogni momento, tuttavia ciò che contribuiscono è comunque prezioso per la descrizione del movimento.

Utilizzando i segni sia della velocità che dell'accelerazione, è possibile sapere se un mobile che si muove su una linea retta accelera o rallenta. In entrambe le situazioni l'accelerazione è presente, poiché la velocità sta cambiando.

Ecco alcune interessanti considerazioni sui segni di queste due grandezze:

• La velocità media e l'accelerazione, entrambe dello stesso segno, significano che visto a livello globale, il cellulare va sempre più veloce.
• La velocità e l'accelerazione con segni diversi è segno di un cellulare che ha piuttosto frenato.

Di solito si pensa che ogni volta che si tratta di un'accelerazione negativa, il cellulare stia frenando. Questo è vero se la velocità del cellulare è positiva. Ma se è negativo, la velocità sta effettivamente aumentando.

Come sempre quando studi il movimento, pensa a casi speciali. Ad esempio, cosa succede quando l'accelerazione media è zero? Significa che il cellulare ha sempre mantenuto la sua velocità costante??

La risposta è no. Il cellulare avrebbe potuto variare la sua velocità nell'intervallo considerato, ma la velocità iniziale e quella finale erano le stesse. Al momento non si conoscono i dettagli di quanto accaduto nell'intervallo, poiché l'accelerazione media non offre maggiori informazioni.

E se l'accelerazione media per_m è uguale all'accelerazione per in qualsiasi momento dell'intervallo di tempo? Questa è una situazione molto interessante chiamata Movimento rettilineo uniformemente variato o MRUV in breve..

Significa che la velocità cambia in modo uniforme nel tempo. Pertanto l'accelerazione è costante. In natura esiste un tale movimento, con cui tutti hanno familiarità: caduta libera.

Caduta libera: un movimento con accelerazione costante

È noto che la terra attira gli oggetti verso il suo centro e che quando uno viene rilasciato ad una certa altezza, subisce l'accelerazione di gravità, il cui valore è approssimativamente costante e pari a 9,8 m / s^Due vicino alla superficie.

Se la resistenza dell'aria non interviene, il movimento è verticale ed è noto come caduta libera. Quando l'accelerazione è costante e scegliendo t₀ = 0, l'equazione per l'accelerazione media diventa:

v_F = v₀ + at = gt (v₀= 0)

Dove a = g = 9,8 m / s^Due

Esercizio risolto

Un oggetto è caduto da un'altezza sufficiente. Trovare la velocità dopo 1,25 secondi.

Risposta

v_o = 0, poiché l'oggetto è stato rilasciato, allora:

v_F = gt = 9,8 x 1,25 m / s = 12,25 m / s, diretto verticalmente verso il suolo. (La direzione verticale verso il basso è stata considerata positiva).

Quando l'oggetto si avvicina al suolo, la sua velocità aumenta di 9,8 m / s per ogni secondo trascorso. La massa dell'oggetto non è coinvolta. Due oggetti diversi, lasciati cadere dalla stessa altezza e contemporaneamente, sviluppano la stessa velocità con cui cadono.

Riferimenti

1. Giancoli, D. Physics. Principi con applicazioni. Sesta edizione. Prentice Hall. 21- 35.
2. Resnick, R. (1999). Fisico. Volume 1. Terza edizione in spagnolo. Messico. Azienda editoriale Continental S.A. de C.V. 20-34.
3. Serway, R., Jewett, J. (2008). Fisica per la scienza e l'ingegneria. Volume 1. 7^ma. Edizione. Messico. Cengage Learning Editors. 21-39.