Il velocità relativa di un oggetto è quello che viene misurato rispetto a un dato osservatore, poiché un altro osservatore può ottenere una misura diversa. La velocità dipende sempre dall'osservatore che la misura.
Pertanto, la velocità di un oggetto misurata da una certa persona sarà la velocità relativa rispetto ad essa. Un altro osservatore può ottenere un valore diverso per la velocità, anche se è lo stesso oggetto.
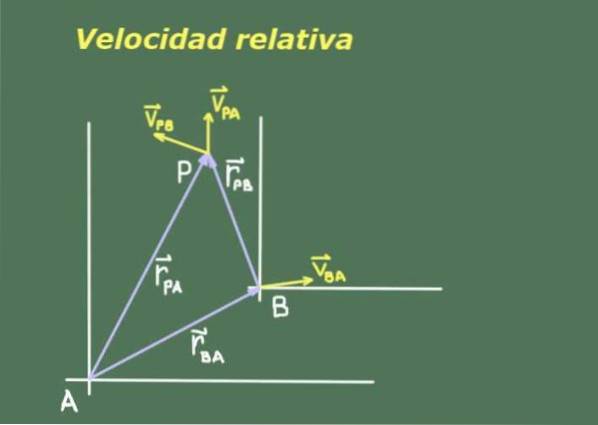
Poiché due osservatori A e B che si muovono l'uno rispetto all'altro possono avere misurazioni diverse di un terzo oggetto in movimento P, è necessario cercare una relazione tra le posizioni e le velocità di P viste da A e B.
La figura 1 mostra due osservatori A e B con i rispettivi sistemi di riferimento, dai quali misurano la posizione e la velocità dell'oggetto P.
Ogni osservatore A e B misura la posizione e la velocità dell'oggetto P in un dato istante di tempo t. Nella relatività classica (o galileiana) il tempo per l'osservatore A è lo stesso dell'osservatore B indipendentemente dalle loro velocità relative.
Questo articolo riguarda la relatività classica che è valida e applicabile alla maggior parte delle situazioni quotidiane in cui gli oggetti hanno velocità molto più lente di quella della luce..
Indichiamo la posizione dell'osservatore B rispetto ad A come rBA. Poiché la posizione è una quantità vettoriale, usiamo il grassetto per indicarla. La posizione dell'oggetto P rispetto ad A è indicata con rPAPÀ e quella dello stesso oggetto P rispetto a B rPB.
Indice articolo
Esiste una relazione vettoriale tra queste tre posizioni che può essere dedotta dalla rappresentazione della figura 1:
rPAPÀ= rPB + rBA
Se la derivata dell'espressione precedente è presa rispetto al tempo t otterremo la relazione tra le velocità relative di ogni osservatore:
VPAPÀ= VPB + VBA
Nell'espressione precedente abbiamo la velocità relativa di P rispetto ad A in funzione della velocità relativa di P rispetto a B e della velocità relativa di B rispetto ad A.
Allo stesso modo, la velocità relativa di P rispetto a B può essere scritta in funzione della velocità relativa di P rispetto ad A e della velocità relativa di A rispetto a B.
VPB= VPAPÀ + VAB
Si noti che la velocità relativa di A rispetto a B è uguale e contraria a quella di B rispetto ad A:
VAB = -VBA
Una macchina percorre un rettilineo, che va da ovest a est, con una velocità di 80 km / h mentre nella direzione opposta (e dall'altra corsia) arriva una moto con una velocità di 100 km / h.
Un ragazzo sta viaggiando sul sedile posteriore dell'auto che vuole conoscere la velocità relativa di una motocicletta che si sta avvicinando a lui. Per scoprire la risposta, il bambino applicherà le relazioni che ha appena letto nella sezione precedente, identificando ogni sistema di coordinate come segue:
-A è il sistema di coordinate di un osservatore sulla strada e rispetto ad esso sono state misurate le velocità di ogni veicolo.
-B è l'auto e P è la motocicletta.
Se si vuole calcolare la velocità della moto P rispetto alla vettura B, verrà applicata la seguente relazione:
VPB= VPAPÀ + VAB=VPAPÀ - VBA
Considerando positiva la direzione ovest-est abbiamo:
VPB= (-100 km / h - 80 km / h) io = -180 km / h io
Questo risultato viene interpretato come segue: la motocicletta si muove rispetto all'auto con una velocità e direzione di 180 km / he direzione -io, cioè da est a ovest.
La moto e l'auto si sono incrociate seguendo la loro corsia. Il bambino sul sedile posteriore dell'auto vede la motocicletta allontanarsi e ora vuole sapere a che velocità si sta allontanando da lui, supponendo che sia la motocicletta che l'auto mantengano le stesse velocità di prima dell'incrocio..
Per conoscere la risposta, il bambino applica la stessa relazione utilizzata in precedenza:
VPB= VPAPÀ + VAB=V PAPÀ - VBA
VPB= -100 km / h io - 80 km / h io = -180 km / h io
E ora la motocicletta si sta allontanando dall'auto con la stessa velocità relativa con cui si stava avvicinando prima che attraversassero..
La stessa motocicletta della parte 2 viene restituita mantenendo la stessa velocità di 100 km / h ma cambiando direzione. Ovvero, l'auto (che prosegue alla velocità di 80 km / h) e la motocicletta si muovono entrambe in direzione positiva est-ovest..
Ad un certo punto la moto sorpassa la macchina, e il bambino sul sedile posteriore dell'auto vuole conoscere la velocità relativa della moto rispetto a lui quando la vede passare..
Per ottenere la risposta, il bambino applica nuovamente le relazioni di moto relativo:
VPB= VPAPÀ + VAB=VPAPÀ - VBA
VPB= +100 km / h io - 80 km / h io = 20 km / h io
Il bambino dal sedile posteriore osserva la motocicletta che sorpassa l'auto alla velocità di 20 km / h.
Una barca a motore attraversa un fiume largo 600 me scorre da nord a sud. La velocità del fiume è di 3 m / s. La velocità della barca rispetto all'acqua del fiume è di 4 m / s in direzione est.
(i) Trova la velocità della barca rispetto alla riva del fiume.
(ii) Indicare la velocità e la direzione della barca rispetto alla terra.
(iii) Calcola il tempo di crossover.
(iv) Fino a che punto si sarà spostato a sud dal punto di partenza.
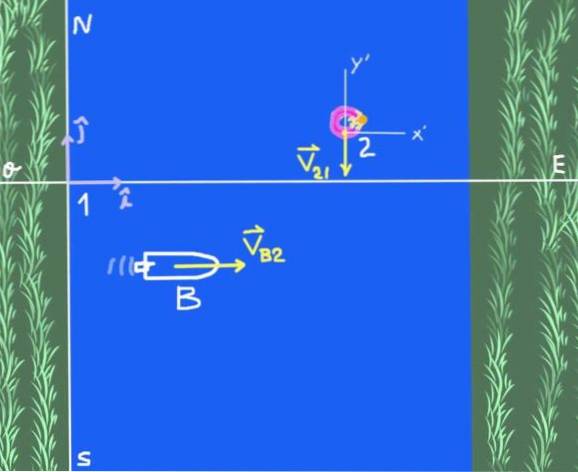
Esistono due sistemi di riferimento: il sistema di riferimento solidale sulla riva del fiume che chiameremo 1 e il sistema di riferimento 2, che è un osservatore che galleggia sull'acqua del fiume. Oggetto di studio è la barca B.
La velocità della barca rispetto al fiume è scritta in forma vettoriale come segue:
VB2 = 4 io SM
La velocità dell'osservatore 2 (zattera sul fiume) rispetto all'osservatore 1 (a terra):
Vventuno = -3 j SM
Vuoi trovare la velocità della barca rispetto alla terra VB1.
VB1 = VB2 + Vventuno
VB1 = (4 io - 3 j) SM
La velocità della barca sarà il modulo della velocità precedente:
|VB1| = (42 + (-3) 2) ½ = 5 m / s
E l'indirizzo sarà:
θ = arctan (-¾) = -36,87º
Il tempo di traversata della barca è il quoziente tra la larghezza del fiume e la componente x della velocità della barca rispetto alla terra.
t = (600 m) / (4 m / s) = 150 s
Per calcolare la deriva che ha avuto l'imbarcazione verso sud, la componente y della velocità dell'imbarcazione rispetto alla terraferma viene moltiplicata per il tempo di traversata:
d = -3 j m / s * 150 s = -450 j m
Lo spostamento verso sud rispetto al punto di partenza è di 450m.
Nessun utente ha ancora commentato questo articolo.