
Calcolo vettoriale normale ed esempio
Il vettore normale è quello che definisce la direzione perpendicolare a qualche entità geometrica in esame, che può essere una curva, un piano o una superficie, ad esempio.
È un concetto molto utile nel posizionamento di una particella in movimento o di una superficie nello spazio. Nel grafico seguente è possibile vedere come è il vettore normale di una curva arbitraria C:
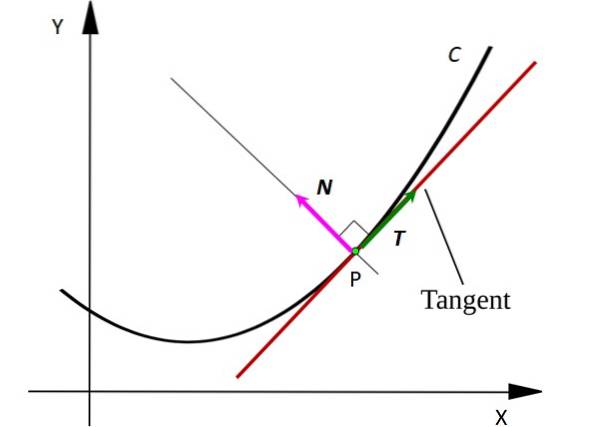
Considera un punto P sulla curva C. Il punto può rappresentare una particella in movimento che si muove lungo un percorso a forma di C. La linea tangente alla curva nel punto P è disegnata in rosso..
Notare che il vettore T è tangente a C in ogni punto, mentre il vettore N è perpendicolare a T y punta al centro di un cerchio immaginario il cui arco è un segmento di C. I vettori sono indicati in grassetto nel testo stampato, per distinguerli da altre quantità non vettoriali.
Il vettore T indica sempre dove si muove la particella, quindi indica la sua velocità. Invece il vettore N punta sempre nella direzione di rotazione della particella, in questo modo indica la concavità della curva C.
Indice articolo
- 1 Come ottenere il vettore normale su un piano?
- 1.1 Il vettore normale dal prodotto vettoriale
- 2 Esempio
- 2.1 Soluzione
- 2.2 Calcolo del prodotto vettoriale AB x AC
- 3 Riferimenti
Come portare il vettore normale a un aereo?
Il vettore normale non è necessariamente un vettore unitario, cioè un vettore il cui modulo è 1, ma in tal caso si chiama vettore unitario normale.
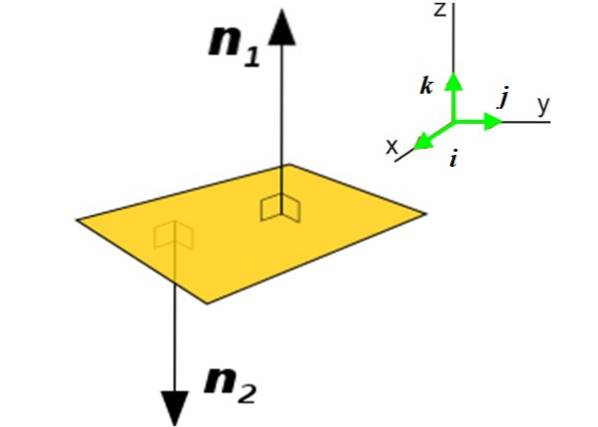
In molte applicazioni è necessario conoscere il vettore normale a un piano invece che a una curva. Questo vettore rivela l'orientamento di detto piano nello spazio. Ad esempio, considera l'aereo P (giallo) della figura:
Ci sono due vettori normali su questo piano: n1 Y nDue. L'uso dell'uno o dell'altro dipenderà dal contesto in cui si trova detto piano. Ottenere il vettore normale a un piano è molto semplice se conosci la sua equazione:
ax + di + cz + d = 0, con per, b, c Y d numeri reali.
Ebbene, un vettore normale a detto piano è dato da:
N = a io + b j + c K
Qui il vettore N È espresso in termini di vettori unitari e perpendicolari tra loro io, j Y K, diretto lungo le tre direzioni che determinano lo spazio X e Z, vedere la figura 2 a destra.
Il vettore normale dal prodotto vettoriale
Una procedura molto semplice per trovare il vettore normale utilizza le proprietà del prodotto vettoriale tra due vettori.
Come è noto, tre punti diversi e non allineati tra loro determinano un piano P. Ora è possibile ottenere due vettori o Y v che appartengono a detto piano avente questi tre punti.
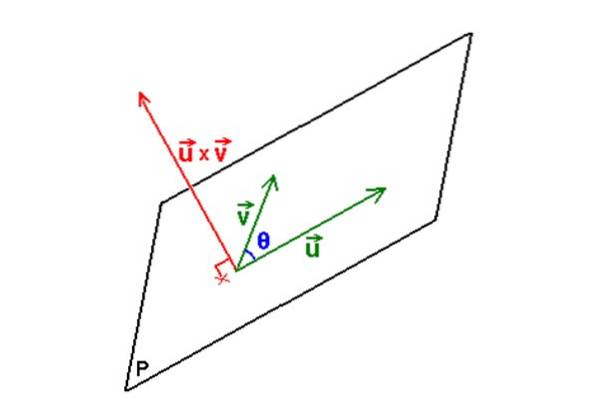
Una volta che hai i vettori, il file prodotto vettoriale o X v è un'operazione il cui risultato è a sua volta un vettore, che ha la proprietà di essere perpendicolare al piano determinato da o Y v.
Conosciuto questo vettore, è indicato come N, e da esso sarà possibile determinare l'equazione del piano grazie all'equazione indicata nella sezione precedente:
N = o X v
La figura seguente illustra la procedura descritta:
Esempio
Trova l'equazione del piano determinata dai punti A (2,1,3); B (0,1,1); C (4,2,1).
Soluzione
Questo esercizio illustra la procedura sopra descritta. Avendo 3 punti, uno di essi viene scelto come origine comune di due vettori che appartengono al piano definito da questi punti. Ad esempio, il punto A viene impostato come origine e vengono costruiti i vettori AB Y AC.
Il vettore AB è il vettore la cui origine è il punto A e il cui punto finale è il punto B. Le coordinate del vettore AB sono determinati rispettivamente sottraendo le coordinate di B dalle coordinate di A:
AB = (0-2) io + (1-1) j + (1-3) K = -2io + 0j -Due K
Procediamo allo stesso modo per trovare il vettore AC:
AC = (4-2) io + (2-1) j + (1-3) K = 2io + j -Due K
Calcolo del prodotto vettoriale AB x AC
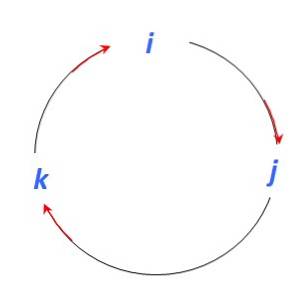
Esistono diverse procedure per trovare il prodotto vettoriale tra due vettori. Questo esempio utilizza una procedura mnemonica che utilizza la figura seguente per trovare i prodotti vettoriali tra i vettori unitari io, j Y K:
Per cominciare è bene ricordare che i prodotti vettoriali tra vettori paralleli sono nulli, quindi:
io X io = 0; j X j = 0; K X K = 0
E poiché il prodotto vettoriale è un altro vettore perpendicolare ai vettori partecipanti, quando ci si sposta nella direzione della freccia rossa abbiamo:
io X j = K ; j X K = io; K X io = j
Se devi muoverti nella direzione opposta alla freccia, aggiungi un segno (-):
j X io = - K; K X j = -io; io X K = -j
In totale è possibile realizzare 9 prodotti vettoriali con i vettori unitari io, j Y K, di cui 3 saranno nulli.
AB X AC = (-2io + 0j -Due K) x (2io + j -Due K) = -4 (io X io) -Due(io X j) +4 (io X K) +0 (j X io) + 0 (j X j) - 0 (j X K) - 4 (K X io)-Due (K X j) + 4 (K X K) = -2K-4j-4j+Dueio = 2io -8j-DueK
Equazione dell'aereo
Il vettore N è stato determinato dal prodotto vettoriale precedentemente calcolato:
N = Dueio -8j-DueK
Quindi a = 2, b = -8, c = -2, il piano cercato è:
ax + di + cz + d = 0 → 2x-8y-2z + d = 0
Il valore di d. Questo è facile se i valori di uno qualsiasi dei punti A, B o C disponibili vengono sostituiti nell'equazione del piano. Scegliendo C per esempio:
x = 4; y = 2; z = 1
Resti:
2,4 - 8,2 - 2,1 + d = 0
-10 + d = 0
d = 10
In breve, la mappa ricercata è:
2x-8y-2z +10 = 0
Il lettore curioso potrebbe chiedersi se lo stesso risultato sarebbe stato ottenuto se invece di fare AB X AC avrebbero scelto di effettuare AC X AB. La risposta è sì, il piano determinato da questi tre punti è unico e ha due vettori normali, come mostrato nella figura 2.
Per quanto riguarda il punto selezionato come origine dei vettori, non c'è problema nella scelta degli altri due.
Riferimenti
- Figueroa, D. (2005). Serie: Fisica per la scienza e l'ingegneria. Volume 1. Cinematica. A cura di Douglas Figueroa (USB). 31- 62.
- Trovare la normale a un aereo. Recupero da: web.ma.utexas.edu.
- Larson, R. (1986). Calcolo e geometria analitica. Mc Graw Hill. 616 - 647.
- Linee e piani in R 3. Recupero da: math.harvard.edu.
- Vettore normale. Recupero da mathworld.wolfram.com.



Nessun utente ha ancora commentato questo articolo.