
Proprietà, applicazioni, esempi della trasformata di Fourier
Il trasformata di Fourier è un metodo di adeguatezza analitica orientato a funzioni integrabili che appartiene alla famiglia di ttrasformato integralmente. Consiste in una ridefinizione delle funzioni F (t) in termini di Cos (t) e Sen (t).
Le identità trigonometriche di queste funzioni, insieme alle loro caratteristiche di derivazione e antiderivazione, servono a definire la trasformata di Fourier attraverso la seguente funzione complessa:
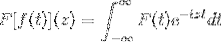
Il che è vero finché l'espressione ha senso, cioè quando l'integrale improprio è convergente. Algebricamente si dice che la trasformata di Fourier sia un omeomorfismo lineare.
Ogni funzione che può essere lavorata con una trasformata di Fourier deve presentare null al di fuori di un parametro definito.
Indice articolo
- 1 Proprietà
- 1.1 Esistenza
- 1.2 Linearità della trasformazione di Fourier
- 1.3 Trasformata di Fourier di una derivata
- 1.4 Differenziazione della trasformata di Fourier
- 1.5 Trasformata di Fourier di una traduzione
- 1.6 Traslazione della trasformata di Fourier
- 1.7 Trasformata di Fourier di un gruppo di scala
- 1.8 Simmetria
- 1.9 Trasformata di Fourier di un prodotto di convoluzione
- 1.10 Continuità e decadimento all'infinito
- 2 Storia
- 3 A cosa serve la trasformata di Fourier?
- 3.1 La serie di Fourier
- 3.2 Altre forme della serie di Fourier
- 4 Applicazioni
- 4.1 Calcolo della soluzione fondamentale
- 4.2 Teoria dei segnali
- 5 esempi
- 5.1 Esempio 1
- 5.2 Esempio 2
- 6 Esercizi proposti
- 7 Riferimenti
Proprietà

La trasformata di Fourier soddisfa le seguenti proprietà:
Esistenza
Verificare l'esistenza della trasformata di Fourier in una funzione f (t) definita nei reali R, i seguenti 2 assiomi devono essere soddisfatti:
- f (t) è continuo a tratti per ogni cosa R
- f (t) è integrabile in R
Linearità della trasformazione di Fourier
Siano M (t) e N (t) due funzioni qualsiasi con trasformate di Fourier definite, con qualsiasi costante aeb.
F [a M (t) + b N (t)] (z) = a F [M (t)] (z) + b F [N (t)] (z)
Il che è supportato anche dalla linearità dell'integrale omonimo.
Trasformata di Fourier di una derivata
Ha una funzione F che è continuo e integrabile in tutti i reali, dove:
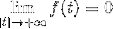
E il derivato di f (f ') è continuo e definito frammentario dappertutto R
La trasformata di Fourier di una derivata è definita dall'integrazione per parti, dalla seguente espressione:
F [f '(t)] (z) = izF [f (t)] (z)
In derivazioni di ordine superiore, verrà applicato in modo omologato, dove per tutti gli n 1 abbiamo:
F [f n'(t)] (z) = (iz)nF [f (t)] (z)
Differenziazione della trasformata di Fourier
Ha una funzione F che è continuo e integrabile in tutti i reali, dove:
io (d / dz)F [f (t)] (z) = F [t. f (t)] (z)
Trasformata di Fourier di una traduzione
Per tutti θ che appartiene a un insieme S e T che appartiene all'insieme S ', abbiamo:
F [ τper θ] = e-iay F [ θ] F [ τperT ] = e-iax F [ T]
Con τper lavorando come operatore di traduzione sul vettore a.
Traslazione della trasformata di Fourier
Per tutti θ che appartiene a un insieme S e T che appartiene all'insieme S ', abbiamo:
τper F [θ] = F [e-iax.θ] τper F [T ] = F [e-iay . T]
Per tutti per che appartiene a R
Trasformata di Fourier di un gruppo di scala
Per tutti θ che appartiene a un insieme S. T che appartiene all'insieme S '
λ appartenente a R - 0 devi:
F [θ (λx)] = (1 / | λ |) F [θ] (Y /λ)
F [T (λx)] = (1 / | λ |) F [T] (y / λ)
sì F è una funzione continua e chiaramente integrabile, dove a> 0. Quindi:
F [f (at)] (z) = (1 / a) F [f (t)] (z / a)
Per dimostrare questo risultato possiamo procedere con il cambio di variabile.
Quando T → + allora s = a → + ∞
Quando T → - allora s = a → - ∞
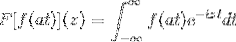
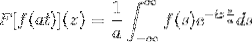
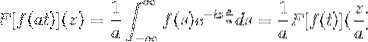
Simmetria
Per studiare la simmetria della trasformata di Fourier, è necessario verificare l'identità di Parseval e la formula di Plancherel.
Abbiamo θ e δ che appartengono a S. Da lì si può dedurre che:
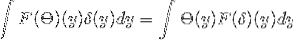
Ottenere
1 / (2π)d F [θ ], F [δ] L'identità di Parseval
1 / (2π)d / 2 || F [θ ] ||LDueRd Formula Plancherel
Trasformata di Fourier di un prodotto di convoluzione
Perseguendo obiettivi simili a quelli della trasformata di Laplace, la convoluzione delle funzioni si riferisce al prodotto tra le loro trasformate di Fourier.
Abbiamo f e g come 2 funzioni limitate, definite e completamente integrabili:
F (f * g) = F (f). F (g)
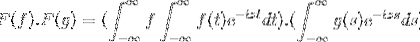
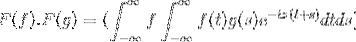
Quindi quando si modifica la variabile
t + s = x; continua con il doppio integrale improprio
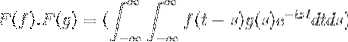
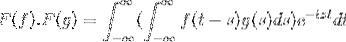
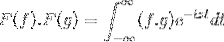
F (f). F (g) = F (f. G)
Continuità e caduta nell'infinito
Per tutti θ che appartiene a R, F [ θ] obbedisce ai criteri di una funzione continua limitata in Rd.
Anche F [ θ] (y) → 0 in C se | y | → ∞
Storia
Questo concetto matematico fu presentato da Joseph B. Fourier nel 1811 mentre sviluppava un trattato sul diffusione del calore. È stato rapidamente adottato da vari rami della scienza e dell'ingegneria.
Si è affermato come principale strumento di lavoro nello studio di equazioni con derivate parziali, anche confrontandolo con il rapporto di lavoro esistente tra i Trasformata di Laplace ed equazioni differenziali ordinarie.
A cosa serve la trasformata di Fourier?
Serve principalmente a semplificare in modo significativo le equazioni, trasformando le espressioni derivate in elementi di potenza, denotando espressioni differenziali sotto forma di polinomi integrabili..
Nell'ottimizzazione, modulazione e modellazione dei risultati, funge da espressione standardizzata, essendo una risorsa frequente per l'ingegneria dopo diverse generazioni.
La serie di Fourier
Sono serie definite in termini di Coseni e Seni; Servono per facilitare il lavoro con funzioni periodiche generali. Quando vengono applicati, fanno parte delle tecniche per risolvere equazioni alle derivate ordinarie e parziali..
Le serie di Fourier sono ancora più generali della serie di Taylor, perché sviluppano funzioni periodiche discontinue che non hanno una rappresentazione in serie di Taylor..
Altre forme della serie di Fourier
Per comprendere analiticamente la trasformata di Fourier, è importante rivedere gli altri modi in cui la serie di Fourier può essere trovata, fino a quando non possiamo definire la serie di Fourier nella sua notazione complessa.
-Serie di Fourier su una funzione periodo 2L
Molte volte è necessario adattare la struttura di una serie di Fourier a funzioni periodiche il cui periodo è p = 2L> 0 nell'intervallo [-L, L].
-Serie di Fourier in funzioni pari e dispari
Viene considerato l'intervallo [-π, π], che offre vantaggi quando si sfruttano le caratteristiche simmetriche delle funzioni.
Se f è pari, la serie di Fourier è stabilita come una serie di Coseni.
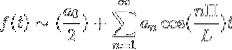
Se f è dispari, la serie di Fourier è stabilita come una serie di Seni.
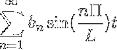
-Notazione complessa della serie di Fourier
Se abbiamo una funzione f (t), che soddisfa tutti i requisiti di sviluppabilità della serie di Fourier, è possibile denotarla nell'intervallo [-t, t] usando la sua notazione complessa:
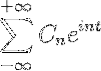
Applicazioni

Calcolo della soluzione fondamentale
La trasformata di Fourier è un potente strumento nello studio delle equazioni alle derivate parziali di tipo lineare a coefficienti costanti. Si applicano ugualmente alle funzioni con domini illimitati.
Come la trasformata di Laplace, la trasformata di Fourier trasforma una funzione di derivata parziale in un'equazione differenziale ordinaria molto più semplice da utilizzare..
Il problema di Cauchy per l'equazione del calore presenta un campo di frequente applicazione della trasformata di Fourier dove viene generata la funzione nucleo di calore o nucleo di Dirichlet.
Per quanto riguarda il calcolo della soluzione fondamentale, vengono presentati i seguenti casi in cui è comune trovare la trasformata di Fourier:
-Equazione di Laplace
-Equazione del calore
-Equazione di Schrödinger
-Equazione delle onde
Teoria dei segnali
La ragione generale per l'applicazione della trasformata di Fourier in questo ramo è principalmente dovuta alla decomposizione caratteristica di un segnale come una sovrapposizione infinita di segnali più facilmente trattabili.
Può essere un'onda sonora o un'onda elettromagnetica, la trasformata di Fourier la esprime in una sovrapposizione di onde semplici. Questa rappresentazione è abbastanza frequente nell'ingegneria elettrica.
D'altra parte, ci sono esempi dell'applicazione della trasformata di Fourier nel campo della teoria dei segnali:
-Problemi di identificazione del sistema. Stabilito f e g
-Problema di consistenza del segnale di uscita
-Problemi con il filtraggio del segnale
Esempi
Esempio 1
Definisci la trasformata di Fourier per la seguente espressione:
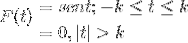
Possiamo anche rappresentarlo nel modo seguente:
F (t) = Sen (t) [H(t + k) - H(t - k) ]
L'impulso rettangolare è definito:
p (t) = H(t + k) - H(t - k)
La trasformata di Fourier viene applicata alla seguente espressione che assomiglia al teorema di modulazione.
f (t) = p (t) Sen (t)
Dove: F [w] = (1/2) i [p (w + 1) - p (w - 1)]
E la trasformata di Fourier è definita da:
F [w] = (1/2) i [(2 / 2w + 1) Sen (k (w + 1)) - (2 / 2w + 1) Sen (k (w-1))]
Esempio 2
Definisci la trasformata di Fourier per l'espressione:
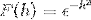
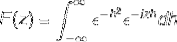
Poiché f (h) è una funzione pari, si può affermare che
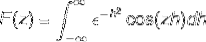
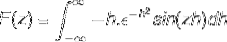
L'integrazione per parti viene applicata selezionando le variabili e i loro differenziali come segue
u = sin (zh) du = z cos (zh) dh
dv = h (e-h)Due v = (e-h)Due / Due
Sostituendo hai
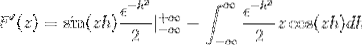
Dopo aver valutato secondo il teorema fondamentale del calcolo
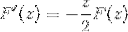
Applicando la conoscenza precedente relativa alle equazioni differenziali del primo ordine, l'espressione è indicata come
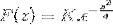
Per ottenere K valutiamo
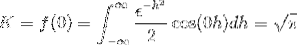
Infine, la trasformata di Fourier dell'espressione è definita come
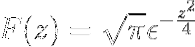
Esercizi proposti
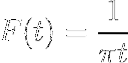
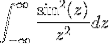
- Ottieni la trasformazione dell'espressione W / (1 + wDue)
Riferimenti
- Duoandikoetxea Zuazo, J., analisi di Fourier. Addison- Wesley Iberoamericana, Università Autonoma di Madrid, 1995.
- Lions, J. L., Analisi matematica e metodi numerici per la scienza e la tecnologia. Springer-Verlag, 1990.
- Lieb, E. H., i kernel gaussiani hanno solo massimizzatori gaussiani. Inventare. Matematica. 102, 179-208, 1990.
- Dym, H., McKean, H. P., Fourier Series and Integrals. Academic Press, New York, 1972.
- Schwartz, L., Théorie des Distributions. Ed. Hermann, Parigi, 1966.



Nessun utente ha ancora commentato questo articolo.