Il lavoro In Fisica è il trasferimento di energia effettuato da una forza quando l'oggetto su cui agisce si muove. Matematicamente assume la forma del prodotto scalare tra i vettori di forza F e spostamento S.
E poiché il prodotto scalare tra due vettori perpendicolari è zero, accade che le forze che si formano a 90 ° con lo spostamento non funzionano, secondo la definizione, poiché:
W = F ● s = F⋅ s⋅ cos θ
Dove W denota lavoro, dalla parola inglese lavoro.
Il vantaggio di definire il lavoro è che è uno scalare, cioè non ha direzione o senso, solo il modulo e la rispettiva unità. Ciò semplifica l'esecuzione dei calcoli che coinvolgono i cambiamenti di energia causati dall'azione delle forze..
La gravità e l'attrito cinetico sono esempi di forze che spesso agiscono sugli oggetti in movimento. Un'altra forza comune è quella normale esercitata da una superficie, ma a differenza di queste, non agisce mai sugli oggetti, in quanto è perpendicolare allo spostamento..
Quando un corpo cade liberamente, la gravità fa un lavoro positivo sul cellulare, facendolo aumentare la sua velocità mentre cade. L'attrito cinetico, invece, ha un effetto completamente opposto, poiché si oppone sempre al movimento, svolge un lavoro negativo che non lo favorisce..
Indice articolo
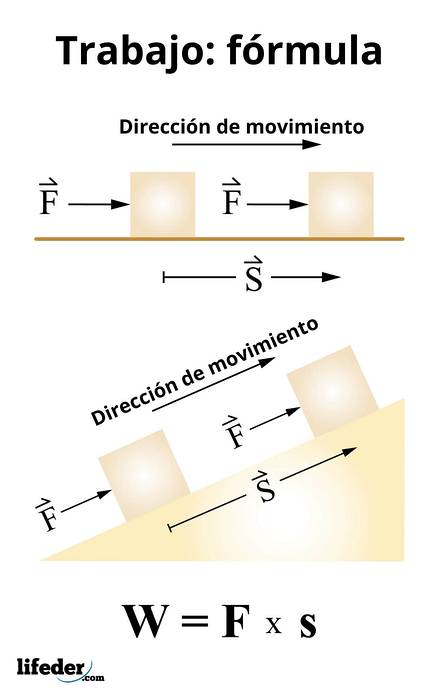
Il lavoro è calcolato da:
W = F ● S
Questa espressione è valida per forze costanti e secondo la definizione di prodotto scalare è equivalente a:
W = F. s. cos θ
Dove θ è l'angolo tra la forza e lo spostamento. Ne consegue, quindi, che solo quelle forze che hanno una componente nella direzione dello spostamento possono lavorare su un corpo.
E diventa anche chiaro che se non c'è movimento, non c'è nemmeno lavoro.
Per quanto riguarda il segno, il lavoro può essere positivo, negativo o zero. Nel caso in cui la forza abbia una componente parallela al moto, il segno del lavoro dipende dal valore di cos θ.
Ci sono alcuni casi particolari che vale la pena considerare:
W = F⋅s cos 0º = F⋅s
W = F⋅s cos 180º = -F⋅s
W = F⋅s cos 90º = 0
A volte la forza applicata non è costante; in tal caso, devi ricorrere al calcolo per trovare il lavoro svolto. Per prima cosa si determina un differenziale di lavoro dW, eseguito su uno spostamento infinitesimale dS:
dW = F⋅dS
Per trovare il valore del lavoro totale svolto da questa forza quando l'oggetto va dal punto A al punto B, è necessario integrare entrambi i lati, in questo modo:
L'unità di lavoro nel Sistema Internazionale è il joule, abbreviato J. L'unità prende il nome dal fisico inglese James Prescott Joule, un pioniere nello studio della termodinamica..
Dall'equazione del lavoro, il joule è definito come 1 newton per metro:
1 J = 1 N⋅m
Il lavoro corrisponde come un'unità libbra forza x piede, a volte chiama piede libbra-forza. È anche un'unità per l'energia, ma va ricordato che il lavoro svolto su un corpo cambia il suo stato energetico e che quindi lavoro ed energia sono equivalenti. Non c'è da stupirsi che abbiano le stesse unità.
L'equivalenza tra il piede libbra-forza e il joule è la seguente:
1 piede-libbra-forza = 1,35582 J
Una nota unità per lavoro ed energia, soprattutto per il settore della refrigerazione e del condizionamento, è la BTU o British Thermal Unit.
1 BTU equivale a 1055 J e 778.169 piedi per libbra-forza.
Esistono altre unità di lavoro che vengono utilizzate in aree specifiche della fisica e dell'ingegneria. Tra questi abbiamo:
Indicato come erg, è l'unità di lavoro nel sistema cegesimale ed è uguale a 1 dyna⋅cm o 1 x 10-7 J.
Abbreviato eV, è comunemente usato nella fisica delle particelle ed è definito come l'energia che un elettrone acquisisce quando si muove attraverso una differenza di potenziale di 1 V.
Appare frequentemente sulle bollette. È il lavoro svolto nell'arco di 1 ora da una sorgente la cui potenza è di 1 kW, pari a 3,6 x 106 J.
Solitamente è correlato all'energia del cibo, anche se di fatto in questo contesto si fa riferimento a a kilocalorie, cioè 1000 calorie. In realtà ci sono diverse unità che ricevono questo nome, quindi il contesto deve essere specificato molto bene.
L'equivalenza tra il joule e 1 calorie termochimiche è:
1 caloria = 4,1840 J.
Quando i corpi scendono, verticalmente o giù da una rampa, il peso fa un lavoro positivo, favorendo il movimento. Invece, ogni volta che un oggetto ascende, la gravità fa un lavoro negativo.
Un campo elettrico uniforme funziona su una carica puntiforme che si muove al suo interno. A seconda del campo e del segno della carica, questo lavoro può essere negativo o positivo.
L'attrito cinetico tra le superfici fa sempre un lavoro negativo sull'oggetto in movimento.
La spinta è una forza che allontana un oggetto da qualcosa. La trazione è una forza che fa avvicinare un oggetto.
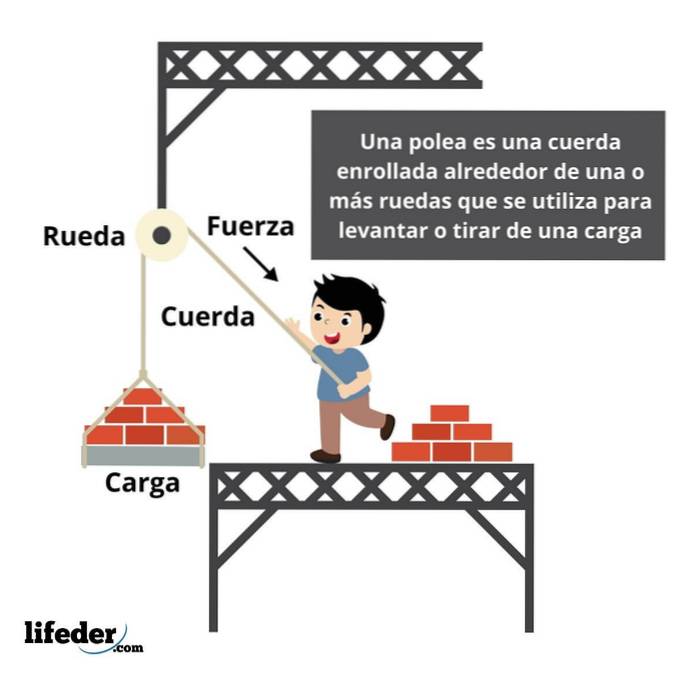
Una puleggia è un sistema utilizzato per trasmettere una forza da una delle sue estremità. In una semplice puleggia, per sollevare il carico, deve essere applicata una forza pari alla resistenza esercitata dall'oggetto.
La normale, come notato sopra, non funziona quando un oggetto appoggiato su una superficie si muove su di essa, anche se la superficie non è piana o se è inclinata..
Un'altra forza che non funziona è la forza magnetica che esercita un campo uniforme sulla particella carica che è perpendicolare ad essa. Il moto della particella risulta essere un moto circolare uniforme, con la forza in direzione radiale. Poiché lo spostamento è perpendicolare alla forza, non agisce sul carico..
Una fune inoltre non funziona su un pendolo sospeso, poiché la tensione in essa è sempre perpendicolare allo spostamento della massa..
Anche la gravità non funziona su un satellite in orbita circolare, per lo stesso motivo dei casi precedenti: è perpendicolare allo spostamento..
In un sistema massa-molla, la forza F che la molla esercita sulla massa ha grandezza F = kx, dove K è la costante primaverile e X la sua compressione o allungamento. È una forza variabile, quindi il lavoro che fa dipende da quanto la molla si allunga o si restringe.
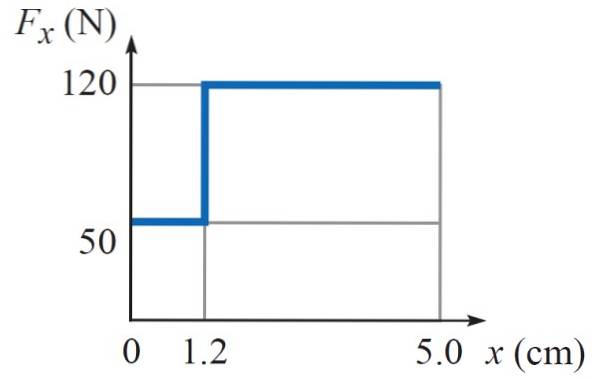
Il grafico seguente mostra il lavoro svolto da una forza variabile FX che dipende dalla posizione X. Questa è la forza esercitata da un martello su un chiodo. La prima parte è la forza utilizzata per inchiodare sulla sezione più morbida del muro e la seconda per finire di piantare il chiodo.
Quanto lavoro deve fare il martello perché il chiodo affondi nel muro per un totale di 5 cm?
La forza esercitata dal martello è variabile, poiché è necessaria una minore intensità (50 N) per spingere il chiodo di 1,2 cm nella parte morbida del muro, mentre nella parte più dura sono necessari 120 N per far affondare il chiodo fino a 5 cm di profondità, come mostrato in tabella.
In questo caso il lavoro è l'integrale:
Dove A = 0 cm e B = 5 cm. Poiché l'integrale è l'area sotto il grafico Fx vs x, è sufficiente trovare quest'area, che corrisponde a due rettangoli, il primo con altezza 50 N e larghezza 1,2 cm, e il secondo con altezza 120 N e larghezza (5 cm - 1,2 cm) = 3,8 cm.
Entrambi vengono calcolati e aggiunti per dare il lavoro totale:
L = 50 N x 1,2 cm + 120 N x 3,8 cm = 516 N. cm = 516 N x 0,01 m = 5,16 J.
Nessun utente ha ancora commentato questo articolo.