
Tassellazioni caratteristiche, tipologie (regolari, irregolari), esempi
Il tassellato sono superfici coperte da una o più figure chiamate piastrelle. Sono ovunque: nelle strade e negli edifici di ogni tipo. Le tessere o tessere sono pezzi piatti, generalmente poligoni con copie congruenti o isometriche, che vengono posizionati seguendo uno schema regolare. In questo modo non si lasciano spazi scoperti e le tessere oi mosaici non si sovrappongono..
Nel caso in cui venga utilizzato un unico tipo di mosaico formato da un poligono regolare, allora c'è un tassellatura regolare, ma se vengono utilizzati due o più tipi di poligoni regolari, si tratta di un file tassellatura semiregolare.

Infine, quando i poligoni che formano la tassellatura non sono regolari, allora è un file tassellazione irregolare.
La tipologia di tassellatura più diffusa è quella formata da mosaici rettangolari e particolarmente quadrati. Nella figura 1 abbiamo un buon esempio.
Indice articolo
- 1 Storia delle tassellature
- 2 Tassellazioni regolari
- 2.1 Nomenclatura
- 2.2 Esempio 1: tassellatura triangolare
- 2.3 Esempio 2: tassellatura quadrata
- 2.4 Esempio 3: tassellatura esagonale
- 3 Tassellazioni semiregolari
- 3.1 Esempio 4: tassellatura tri-esagonale
- 3.2 Esempio 5: tassellatura esagonale smussata
- 3.3 Esempio 6: tassellatura rombi-tri-esagonale
- 4 Tassellazioni irregolari
- 4.1 Esempio 7
- 4.2 Esempio 8
- 4.3 Esempio 9
- 4.4 Esempio 10: tassellatura del Cairo
- 4.5 Esempio 11: tassellatura di Al-Andalus
- 4.6 Esempio 12: tassellazione nei videogiochi
- 5 Riferimenti
Storia delle tassellature
Per migliaia di anni, la tassellatura è stata utilizzata per rivestire pavimenti e pareti di palazzi e templi di diverse culture e religioni..
Ad esempio, la civiltà sumera che fiorì intorno al 3500 a.C. a sud della Mesopotamia, tra i fiumi Eufrate e Tigri, hanno utilizzato tassellature nella loro architettura.

Anche le tassellature hanno suscitato l'interesse di matematici di tutte le età: a partire da Archimede nel III secolo a.C., seguito da Johannes Keplero nel 1619, Camille Jordan nel 1880, fino ai tempi contemporanei con Roger Penrose..
Penrose ha creato una tassellatura non periodica nota come Tassellatura di Penrose. Equesti sono solo alcuni nomi di scienziati che hanno contribuito molto alla tassellatura.
Tassellazioni regolari
Le tassellazioni regolari sono realizzate con un solo tipo di poligono regolare. D'altra parte, affinché la tassellatura sia considerata regolare, ogni punto del piano deve:
-Appartengono all'interno del poligono
-O al bordo di due poligoni adiacenti
-Infine può appartenere al vertice comune di almeno tre poligoni.
Con le limitazioni di cui sopra si può dimostrare che solo triangoli equilateri, quadrati ed esagoni possono formare una tassellatura regolare.
Nomenclatura
Esiste una nomenclatura per indicare le tassellazioni che consiste nell'elencare in senso orario e separati da un punto, il numero di lati dei poligoni che circondano ogni nodo (o vertice) della tassellatura, partendo sempre dal poligono con il numero più basso. lati.
Questa nomenclatura si applica alle tassellazioni regolari e semiregolari.
Esempio 1: tassellatura triangolare
La figura 3 mostra una tassellatura triangolare regolare. Va notato che ogni nodo della tassellatura triangolare è il vertice comune di sei triangoli equilateri.
Il modo per denotare questo tipo di tassellatura è 3.3.3.3.3.3, che è anche indicato con 36.

Esempio 2: tassellatura quadrata
La figura 4 mostra una tassellatura regolare composta solo da quadrati. Va notato che ogni nodo nella tassellatura è circondato da quattro quadrati congruenti. La notazione che viene applicata a questo tipo di tassellatura quadrata è: 4.4.4.4 o in alternativa 44

Esempio 3: tassellatura esagonale
In una tassellatura esagonale ogni nodo è circondato da tre esagoni regolari come mostrato nella figura 5. La nomenclatura per una tassellazione esagonale regolare è 6.6.6 o in alternativa 63.

Tassellazioni semiregolari
Le tassellazioni semiregolari o di Archimede sono costituite da due o più tipi di poligoni regolari. Ogni nodo è circondato dai tipi di poligoni che compongono la tassellatura, sempre nello stesso ordine, e la condizione del bordo è completamente condivisa con il vicino..
Sono presenti otto tassellature semiregolari:
- 3.6.3.6 (tassellatura tri-esagonale)
- 3.3.3.3.6 (tassellatura esagonale smussata)
- 3.3.3.4.4 (tassellatura triangolare allungata)
- 3.3.4.3.4 (tassellatura quadrata smussata)
- 3.4.6.4 (tassellatura rombo-tri-esagonale)
- 4.8.8 (tassellazione quadrata troncata)
- 3.12.12 (tassellatura esagonale troncata)
- 4.6.12 (tassellazione tri-esagonale troncata)
Di seguito sono riportati alcuni esempi di tassellazioni semiregolari.
Esempio 4: tassellatura tri-esagonale
È quello composto da triangoli equilateri ed esagoni regolari nella struttura 3.6.3.6, il che significa che un nodo della tassellatura è circondato (fino a completare un giro) da un triangolo, un esagono, un triangolo e un esagono. La figura 6 mostra una tale tassellatura.

Esempio 5: tassellatura esagonale smussata
Come la tassellatura nell'esempio precedente, anche questa è composta da triangoli ed esagoni, ma la loro distribuzione attorno a un nodo è 3.3.3.3.6. La figura 7 illustra chiaramente questo tipo di tassellatura.

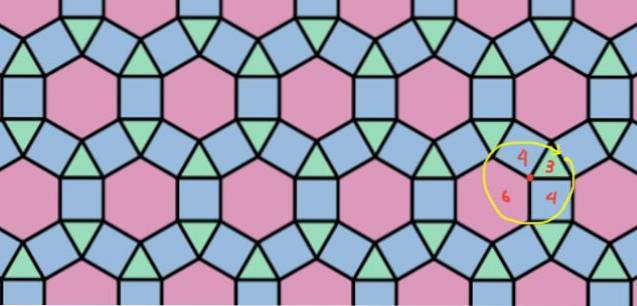
Esempio 6: tassellazione rombi-tri-esagonale
È una tassellatura composta da triangoli, quadrati ed esagoni, nella configurazione 3.4.6.4, che è mostrata in figura 8.
Tassellazioni irregolari
Le tassellazioni irregolari sono quelle che sono formate da poligoni irregolari o da poligoni regolari ma che non soddisfano il criterio che un nodo sia un vertice di almeno tre poligoni.
Esempio 7
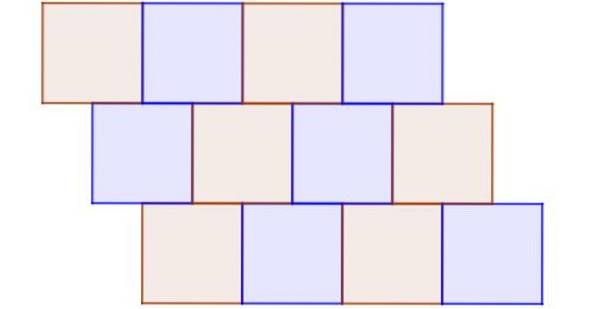
La figura 9 mostra un esempio di tassellatura irregolare, in cui tutti i poligoni sono regolari e congruenti. È irregolare perché un nodo non è un vertice comune di almeno tre quadrati e ci sono anche quadrati vicini che non condividono completamente un bordo.
Esempio 8
Il parallelogramma affianca una superficie piana, ma a meno che non sia un quadrato non può formare una tassellatura regolare.

Esempio 9
Esagoni irregolari con simmetria centrale tassellano una superficie piana, come mostrato nella figura seguente:

Esempio 10: tassellatura del Cairo
Si tratta di una tassellatura molto interessante, composta da pentagoni con lati di uguale lunghezza ma con angoli disuguali, due dei quali sono diritti e gli altri tre hanno 120º ciascuno..
Il suo nome deriva dal fatto che questa tassellatura si trova nella pavimentazione di alcune strade del Cairo in Egitto. La figura 12 mostra la tassellatura del Cairo.

Esempio 11: tassellatura di Al-Andalus
Le tassellature durante alcune parti dell'Andalusia e del Nord Africa sono caratterizzate da geometria ed epigrafia, oltre ad elementi ornamentali come la vegetazione..
La tassellatura di palazzi come quello dell'Alhambra era costituita da piastrelle composte da pezzi di ceramica di molti colori, con forme multiple (se non infinite) che sprigionavano motivi geometrici..

Esempio 12: tassellazione nei videogiochi
Conosciuto anche come tesellation, è una delle novità più popolari nei videogiochi. Si tratta della creazione di texture per simulare la tassellazione dei diversi scenari che compaiono nel simulatore.
Questo è il chiaro riflesso che questi rivestimenti continuano ad evolversi, oltrepassando i confini della realtà..
Riferimenti
- Goditi la matematica. Mosaici. Estratto da: gustolasmatematicas.com
- Rubiños. Le tassellature hanno risolto gli esempi. Estratto da: matematicasn.blogspot.com
- Weisstein, Eric W. "tassellazione demiregolare". Weisstein, Eric W, ed. MathWorld. Wolfram Research.
- Wikipedia. Tassellazione. Estratto da: es.wikipedia.com
- Wikipedia. Tessellazione regolare. Estratto da: es.wikipedia.com


Nessun utente ha ancora commentato questo articolo.