
Teorema di Thévenin in cosa consiste, applicazioni ed esempi
Il Teorema di Thévenin afferma che un circuito con terminali A e B può essere sostituito da uno equivalente costituito da una sorgente e una resistenza in serie, i cui valori danno la stessa differenza di potenziale tra A e B e la stessa impedenza del circuito originale.
Questo teorema fu reso noto nel 1883 dall'ingegnere francese Léon Charles Thévenin, ma si sostiene che sia stato enunciato trent'anni prima dal fisico tedesco Hermann von Helmholtz.

La sua utilità sta nel fatto che, anche quando il circuito originale è complesso o sconosciuto, ai fini di un carico o di un'impedenza che viene posto tra i terminali A e B, il semplice circuito equivalente di Thévenin si comporta allo stesso modo dell'originale.
Indice articolo
- 1 Come si calcola la tensione equivalente passo dopo passo?
- 1.1 - Sperimentalmente
- 1.2 - Risolvere il circuito
- 2 Applicazioni del teorema di Thévenin (parte I)
- 2.1 Esempio 1a (calcolo graduale della tensione equivalente)
- 2.2 Esempio 1b (corrente nel carico utilizzando l'equivalente Thévenin)
- 3 Dimostrazione del teorema di Thévenin
- 4 Applicazione del teorema di Thévenin (parte II)
- 4.1 Esempio 2a (resistenza equivalente Thévenin)
- 4.2 Esempio 2b
- 4.3 Esempio 2c
- 5 Applicazione del teorema di Thévenin (parte III)
- 5.1 Esempio 3
- 6 Riferimenti
Come si calcola la tensione equivalente passo dopo passo?
La differenza di tensione o potenziale del circuito equivalente può essere ottenuta nei seguenti modi:
- Sperimentalmente
Ottenere il voltaggio Thévenin equivalente
Se si tratta di un dispositivo o di un'apparecchiatura che si trova in una "scatola nera", la differenza di potenziale tra i terminali A e B viene misurata con un voltmetro o un oscilloscopio. È molto importante che nessun carico o impedenza sia posto tra i terminali A e B.
Un voltmetro o un oscilloscopio non rappresentano alcun carico sui terminali, poiché entrambi i dispositivi hanno un'impedenza molto grande (idealmente infinita) e sarebbe come se i terminali A e B fossero senza carico. La tensione o tensione ottenuta in questo modo è la tensione equivalente di Thévenin.
Ottenere l'impedenza equivalente di Thévenin
Per ottenere l'impedenza equivalente da una misura sperimentale, una resistenza nota viene posta tra i terminali A e B e la caduta di tensione o il segnale di tensione viene misurata con un oscilloscopio..
Dalla caduta di tensione nella resistenza nota tra i terminali si può ricavare la corrente che la attraversa.
Il prodotto della corrente ottenuta con la resistenza equivalente più la caduta di tensione misurata nella resistenza nota è uguale alla tensione di Thévenin equivalente precedentemente ottenuta. Da questa uguaglianza viene eliminata l'impedenza Thévenin equivalente.
- Risolvere il circuito
Calcolo della tensione equivalente Thévenin
Innanzitutto, qualsiasi carico o impedenza viene scollegato dai terminali A e B..
Come è noto il circuito, la teoria della maglia o le leggi di Kirchhoff vengono applicate per trovare la tensione ai terminali. Questa tensione sarà l'equivalente di Thévenin.
Calcolo dell'impedenza equivalente di Thévenin
Per ottenere l'impedenza equivalente si procede a:
- Sostituire le sorgenti di tensione del circuito originale con cortocircuiti "impedenza zero" e le sorgenti di corrente del circuito originale con quelle aperte "impedenza infinita".
- Quindi l'impedenza equivalente viene calcolata seguendo le regole delle impedenze in serie e delle impedenze in parallelo.
Applicazioni del teorema di Thévenin (parte I)
Applicheremo il teorema di Thévenin per risolvere alcuni circuiti. In questa prima parte consideriamo un circuito che ha solo sorgenti di tensione e resistenze.
Esempio 1a (calcolo graduale della tensione equivalente)
La figura 2 mostra il circuito che si trova in una scatola celeste che ha due batterie di forza elettromotrice V1 e V2 rispettivamente e resistenze R1 e R2, il circuito ha i terminali A e B in cui è possibile collegare un carico.
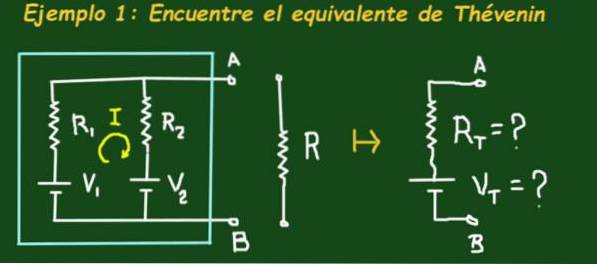
L'obiettivo è trovare il circuito equivalente di Thévenin, ovvero determinare i valori Vt e Rt del circuito equivalente. Applicare i seguenti valori: V1 = 4V, V2 = 1V, R1 = 3Ω, R2 = 6Ω e R = 1Ω.
Soluzione passo passo
Passo 1
Determineremo la tensione ai terminali A e B quando non viene posto alcun carico su di essi.
Passo 2
Il circuito da risolvere è costituito da un'unica maglia attraverso la quale circola una corrente I che abbiamo preso positiva in senso orario.
Passaggio 3
Passiamo attraverso la mesh iniziando dall'angolo in basso a sinistra. Il percorso porta alla seguente equazione:
V1 - I * R1 - I * R2 - V2 = 0
Passaggio 4
Risolviamo per la corrente di maglia I e otteniamo:
I = (V1 -V2) / (R1 + R2) = (4V - 1V) / (3Ω + 6Ω) = ⅓ A
Passaggio 5
Con la corrente di maglia possiamo determinare la differenza di tensione tra A e B, che è:
Vab = V1 - I * R1 = 4V - ⅓ A * 3Ω = 3V
Cioè, la tensione equivalente di Thevenin è: Vt = 3V.
Passaggio 6 (resistenza equivalente Thévenin)
Procediamo ora al calcolo della resistenza equivalente di Thévenin, per la quale e come accennato in precedenza, le sorgenti di tensione vengono sostituite da un cavo.
In tal caso, abbiamo solo due resistori in parallelo, quindi la resistenza equivalente di Thévenin è:
Rt = (R1 * R2) / (R1 + R2) = (3Ω * 6Ω) / (3Ω + 6Ω) = 2Ω
Esempio 1b (corrente nel carico utilizzando l'equivalente Thévenin)
Collegare come carico ai terminali A e B una resistenza R = 1Ω al circuito equivalente e trovare la corrente che scorre attraverso detto carico.
Soluzione
Quando la resistenza R è collegata al circuito equivalente di Thevenin, abbiamo un circuito semplice che consiste in una sorgente Vt una resistenza Rt in serie con la resistenza R.
Chiameremo Ic la corrente che scorre attraverso il carico R, in modo che l'equazione della mesh sia simile a questa:
Vt - Ic * Rt - Ic * R = 0
da cui segue che Ic è dato da:
Ic = Vt / (Rt + R) = 3V / (2Ω + 1Ω) = 1 A
Dimostrazione del teorema di Thévenin
Per verificare che il teorema di Thévenin sia valido, collega R al circuito originale e trova la corrente che scorre attraverso R applicando la legge della mesh al circuito risultante.
Il circuito risultante rimane e le sue equazioni mesh rimangono come mostrato nella figura seguente:
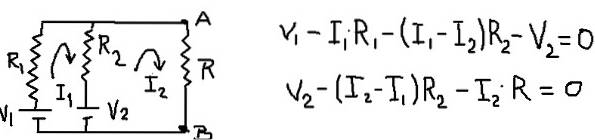
Aggiungendo le equazioni di maglia, è possibile trovare la corrente di maglia I1 in funzione della corrente I2. Quindi viene sostituito nella seconda equazione mesh e viene lasciata un'equazione con I2 come unica incognita. La tabella seguente mostra le operazioni.
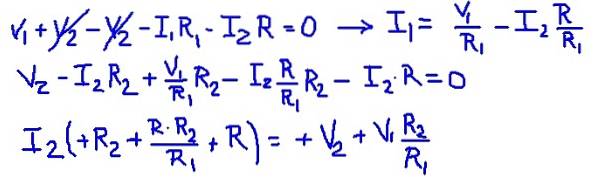
Quindi si sostituiscono i valori della resistenza e delle tensioni delle sorgenti, ottenendo il valore numerico della corrente di maglia I2.

La corrente di maglia I2 è la corrente che attraversa la resistenza di carico R e il valore trovato di 1 A coincide pienamente con quello precedentemente trovato con l'equivalente circuito di Thévenin..
Applicazione del teorema di Thévenin (parte II)
In questa seconda parte, il teorema di Thévenin verrà applicato in un circuito che ha sorgenti di tensione, sorgente di corrente e resistenze.
Esempio 2a (resistenza equivalente Thévenin)
L'obiettivo è determinare il circuito equivalente di Thévenin corrispondente al circuito nella figura seguente, quando i terminali sono privi della resistenza di 1 ohm, si posiziona la resistenza e si determina la corrente che circola attraverso di essa.
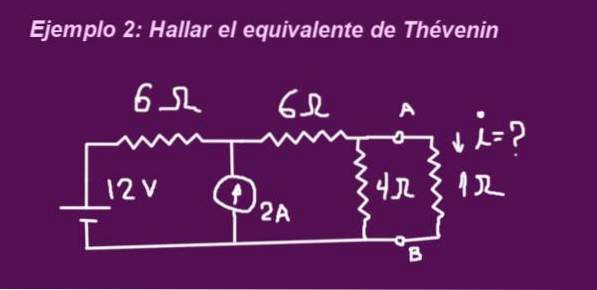
Soluzione
Per trovare la resistenza equivalente, rimuovere la resistenza di carico (in questo caso 1 ohm). Inoltre, le sorgenti di tensione sono sostituite da un cortocircuito e le sorgenti di corrente da un circuito aperto..
In questo modo, il circuito per il quale verrà calcolata la resistenza equivalente è quello mostrato di seguito:
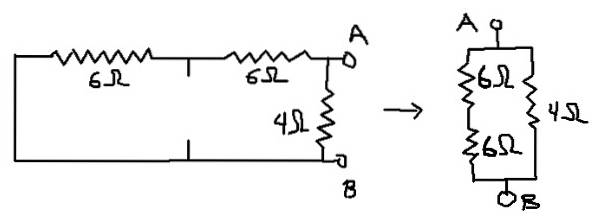
Rab = (12Ω * 4Ω) / (12Ω + 4Ω) = 3Ω che è la resistenza equivalente di Thevenin (Rth).
Esempio 2b
Calcola la tensione equivalente di Thévenin.
Soluzione
Per calcolare la tensione equivalente di Thévenin consideriamo il seguente circuito, in cui collocheremo le correnti in I1 e I2 nei rami indicati nella figura seguente:
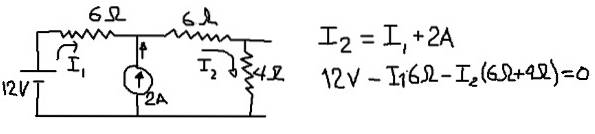
La figura precedente mostra l'equazione dei nodi correnti e l'equazione delle tensioni quando viene attraversata la maglia esterna. Dalla seconda delle equazioni si azzera la corrente I1:
I1 = 2 - I2 * (5/3)
Questa equazione è sostituita nell'equazione dei nodi:
I2 = 2 - (5/3) I2 + 2 ===> I2 (8/3) = 4 ===> I2 = 12/8 = 1,5 A
Ciò significa che la caduta di tensione attraverso il resistore da 4 ohm è di 6 volt..
In breve, la tensione di Thévenin è Vth = 6 V..
Esempio 2c
Trovare il circuito equivalente di Thevenin e la corrente nel resistore di carico.
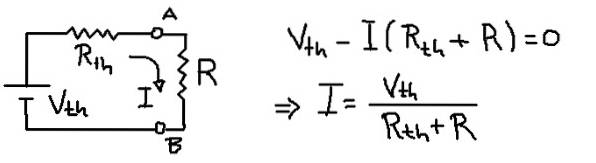
Soluzione
La figura precedente mostra il circuito equivalente di Thévenin con la resistenza di carico R. Dall'equazione della tensione nella maglia si deduce la corrente I che scorre attraverso la resistenza di carico R.
I = Vth / (Rth + R) = 6V / (3Ω + 1Ω) = 1,5 A.
Applicazione del teorema di Thévenin (parte III)
In questa terza parte dell'applicazione del teorema di Thévenin, si considera un circuito a corrente alternata che contiene una sorgente di tensione alternata, un condensatore, un'induttanza e una resistenza..
Esempio 3
L'obiettivo è trovare il circuito di Thévenin equivalente al seguente circuito:
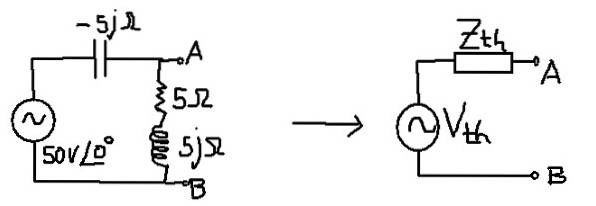
Soluzione
L'impedenza equivalente corrisponde a quella del condensatore in parallelo con la combinazione in serie della resistenza e dell'induttanza.
L'inverso dell'impedenza equivalente è dato da:
Zeq ^ -1 = (-5j) ^ - 1 + (5 + 5j) ^ - 1 = (1/5) j + ((1/10 + (1/10) j) = (1/10 + 3 / 10 j) Mho
E l'impedenza equivalente sarà quindi:
Zeq = (1-3 j) Ohm
La corrente complessa I può essere derivata dall'equazione della mesh:
50V∠0 - I (-5 j + 5 + 5j) = 50V∠0 - I * 5 = 0 ===> I = 10A ∠0
Ora viene calcolata la caduta di tensione nella resistenza più l'induttanza, ovvero la tensione Vab che sarà la tensione di Thévenin equivalente:
Vab = I * (5 + 5 j) Ω = 10A ∠0 * 5Ω∠45º = 50V∠45º
In altre parole, la tensione equivalente ha lo stesso valore di picco della sorgente originale ma è sfasata di 45 gradi: Vth = 50V∠45º
Riferimenti
- Tutorial di elettronica, teorema di Thevenin. Estratto da: electronics-tutorials.ws
- Domande e risposte sulla teoria della rete. Teorema di Thevenin. Estratto da: sanfoundry.com
- Teorema di Thevenin. Procedura passo passo. Estratto da: electrictechnology.org
- Teorema di Thevenin. Esempio risolto passo dopo passo. Estratto da: electricsimple.blogspot.com
- Workshop sui teoremi di Thevenin e Norton. Recupero da: web.iit.edu
- Wikipedia. Teorema di Thévenin. Estratto da: wikipedia.com



Nessun utente ha ancora commentato questo articolo.