
Dimostrazione, applicazione ed esercizi del teorema di Euclide
Il Teorema di Euclide dimostra le proprietà di un triangolo rettangolo tracciando una linea che lo divide in due nuovi triangoli rettangoli simili tra loro e, a loro volta, simili al triangolo originale; poi, c'è una relazione di proporzionalità.
Euclide fu uno dei più grandi matematici e geometrici dell'età antica che eseguì diverse dimostrazioni di importanti teoremi. Uno dei principali è quello che porta il suo nome, che ha avuto un'ampia applicazione.

È stato così perché, attraverso questo teorema, spiega in modo semplice le relazioni geometriche esistenti nel triangolo rettangolo, dove le gambe di questo sono legate alle loro proiezioni nell'ipotenusa..
Indice articolo
- 1 Formule e prove
- 1.1 Teorema dell'altezza
- 1.2 Teorema della gamba
- 2 Relazione tra i teoremi di Euclide
- 3 esercizi risolti
- 3.1 Esempio 1
- 3.2 Esempio 2
- 4 Riferimenti
Formule e dimostrazioni
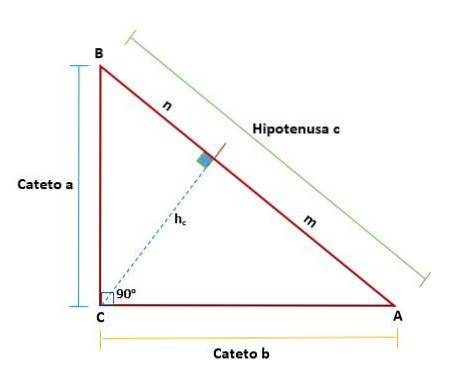
Il teorema di Euclide propone che in ogni triangolo rettangolo, quando viene tracciata una linea - che rappresenta l'altezza che corrisponde al vertice dell'angolo retto rispetto all'ipotenusa - si formano due triangoli rettangoli dall'originale.
Questi triangoli saranno simili tra loro e saranno anche simili al triangolo originale, il che significa che i loro lati simili sono proporzionali tra loro:
Gli angoli dei tre triangoli sono congruenti; ovvero, quando vengono ruotati di 180 gradi attorno al loro vertice, un angolo coincide con l'altro. Ciò implica che saranno tutti uguali.
In questo modo, la somiglianza che esiste tra i tre triangoli può essere verificata anche dall'uguaglianza dei loro angoli. Dalla somiglianza dei triangoli, Euclide stabilisce le proporzioni di questi da due teoremi:
- Teorema dell'altezza.
- Teorema della gamba.
Questo teorema ha un'ampia applicazione. Nell'antichità veniva utilizzato per calcolare altezze o distanze, rappresentando un grande progresso per la trigonometria.
Attualmente è applicato in varie aree basate sulla matematica, come ingegneria, fisica, chimica e astronomia, tra molte altre aree..
Teorema dell'altezza
In questo teorema si stabilisce che in qualsiasi triangolo rettangolo, l'altezza ricavata dall'angolo retto rispetto all'ipotenusa è la media proporzionale geometrica (il quadrato dell'altezza) tra le proiezioni delle gambe che determina sull'ipotenusa.
Cioè, il quadrato dell'altezza sarà uguale alla moltiplicazione delle gambe proiettate che formano l'ipotenusa:
hcDue = m * n
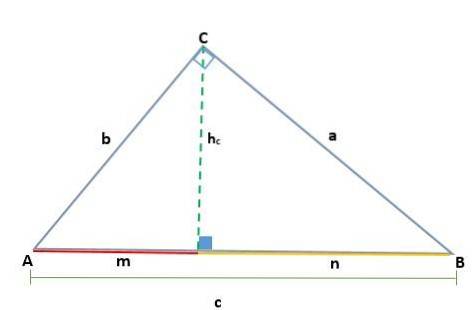
Dimostrazione
Dato un triangolo ABC, che è proprio al vertice C, tracciare l'altezza genera due triangoli rettangoli simili, ADC e BCD; quindi, i loro lati corrispondenti sono proporzionali:
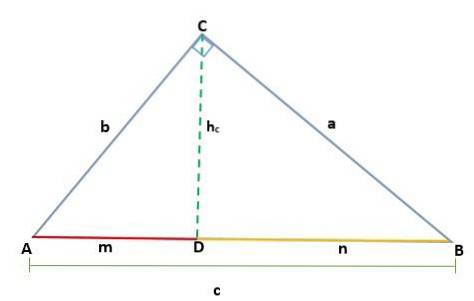
In modo tale che l'altezza hc che corrisponde al segmento CD, corrisponde all'ipotenusa AB = c, quindi abbiamo:
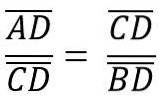
A sua volta, ciò corrisponde a:
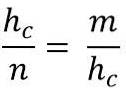
Risolvendo per l'ipotenusa (hc), per moltiplicare i due membri dell'uguaglianza, dobbiamo:
hc * hc = m * n
hcDue = m * n
Pertanto, il valore dell'ipotenusa è dato da:
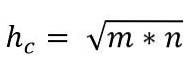
Teorema della gamba
In questo teorema si stabilisce che, in ogni triangolo rettangolo, la misura di ciascuna gamba sarà la media proporzionale geometrica (il quadrato di ciascuna gamba) tra la misura dell'ipotenusa (completa) e la proiezione di ciascuna su di essa:
bDue = c * m
perDue = c* n
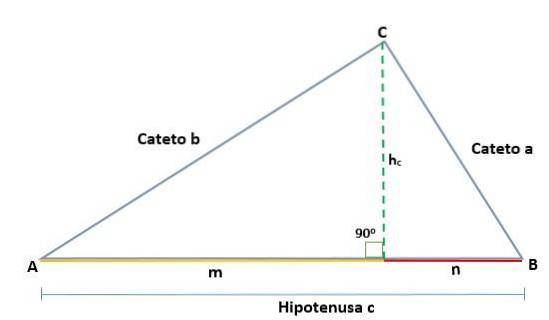
Dimostrazione
Dato un triangolo ABC, che è proprio al vertice C, in modo tale che la sua ipotenusa sia c, quando si traccia l'altezza (h) si determinano le proiezioni delle gambe aeb, che sono rispettivamente i segmenti me n, e che si trovano sull'ipotenusa.
Quindi, abbiamo che l'altezza disegnata sul triangolo rettangolo ABC genera due triangoli rettangoli simili, ADC e BCD, in modo che i lati corrispondenti siano proporzionali, in questo modo:
DB = n, che è la proiezione della gamba CB sull'ipotenusa.
AD = m, che è la proiezione della gamba AC sull'ipotenusa.
Quindi, l'ipotenusa c è determinata dalla somma delle gambe delle sue proiezioni:
c = m + n
A causa della somiglianza dei triangoli ADC e BCD, abbiamo:
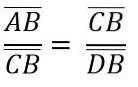
Quanto sopra è lo stesso di:
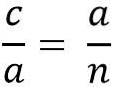
Risolvendo per la gamba "a" per moltiplicare i due membri dell'uguaglianza, abbiamo:
per * a = c * n
perDue = c * n
Pertanto, il valore della gamba "a" è dato da:
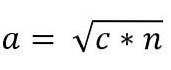
Allo stesso modo, a causa della somiglianza dei triangoli ACB e ADC, abbiamo:
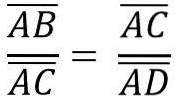
Quanto sopra è uguale a:
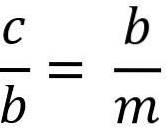
Risolvendo per la gamba "b" per moltiplicare i due membri dell'uguaglianza, abbiamo:
b * b = c * m
bDue = c * m
Pertanto, il valore della gamba "b" è dato da:
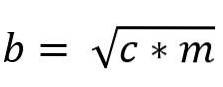
Relazione tra i teoremi di Euclide
I teoremi con riferimento all'altezza e alle gambe sono tra loro correlati perché la misura di entrambi è fatta rispetto all'ipotenusa del triangolo rettangolo.
Attraverso la relazione dei teoremi di Euclide si può anche trovare il valore dell'altezza; questo è possibile risolvendo i valori di m e n dal teorema di gamba e sono sostituiti nel teorema di altezza. In questo modo, si accerta che l'altezza sia uguale alla moltiplicazione delle gambe, divisa per l'ipotenusa:
bDue = c * m
m = bDue ÷ c
perDue = c * n
n = aDue ÷ c
Nel teorema dell'altezza sostituiamo m e n:
hcDue = m * n
hcDue = (bDue ÷ c) * (perDue ÷ c)
hc = (bDue * perDue) ÷ c
Esercizi risolti
Esempio 1
Dato il triangolo ABC, proprio in A, determinare la misura di AC e AD, se AB = 30 cm e BD = 18 cm
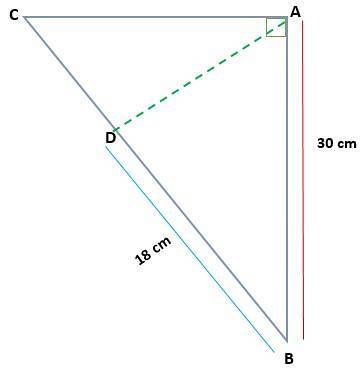
Soluzione
In questo caso abbiamo le misure di una delle gambe proiettate (BD) e di una delle gambe del triangolo originale (AB). In questo modo, il teorema della gamba può essere applicato per trovare il valore della gamba BC.
ABDue = BD * AVANTI CRISTO
(30)Due = 18 * AVANTI CRISTO
900 = 18 * AVANTI CRISTO
AC = 900 ÷ 18
BC = 50 cm
Il valore della gamba CD può essere trovato sapendo che BC = 50:
CD = BC - BD
CD = 50-18 = 32 cm
Ora è possibile determinare il valore della gamba AC, applicando nuovamente il teorema della gamba:
ACDue = CD * BD
ACDue = 32 * cinquanta
ACDue = 160
AC = √1600 = 40 cm
Per determinare il valore dell'altezza (AD) viene applicato il teorema dell'altezza, poiché sono noti i valori delle gambe proiettate CD e BD:
ANNO DOMINIDue = 32 * 18
ANNO DOMINIDue = 576
AD = √576
AD = 24 cm
Esempio 2
Determina il valore dell'altezza (h) di un triangolo MNL, proprio in N, conoscendo le misure dei segmenti:
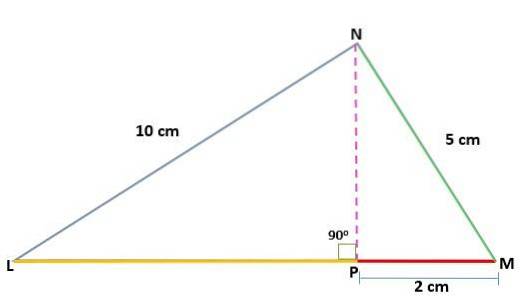
NL = 10 cm
MN = 5 cm
PM = 2 cm
Soluzione
Abbiamo la misura di una delle gambe proiettata sull'ipotenusa (PM), così come le misure delle gambe del triangolo originale. In questo modo, il teorema della gamba può essere applicato per trovare il valore dell'altra gamba proiettata (LN):
NLDue = PM * LM
(10)Due = 5 * LM
100 = 5 * LM
PL = 100 ÷ 5 = 20
Poiché il valore delle gambe e dell'ipotenusa è già noto, attraverso la relazione dei teoremi dell'altezza e delle gambe, si può determinare il valore dell'altezza:
NL = 10
MN = 5
LM = 20
h = (bDue * perDue) ÷ c.
h = (10Due * 5Due) ÷ (venti)
h = (100 * 25) ÷ (venti)
h = 2500 ÷ venti
h = 125 cm.
Riferimenti
- Braun, E. (2011). Caos, frattali e cose strane. Fondo di cultura economica.
- Cabrera, V. M. (1974). Matematica moderna, volume 3.
- Daniel Hernandez, D. P. (2014). 3 ° anno di matematica. Caracas: Santillana.
- Encyclopaedia Britannica, I. (Millenovecentonovantacinque). Enciclopedia ispanica: Macropedia. Editori dell'Enciclopedia Britannica.
- Euclide, R. P. (1886). Elementi di geometria di Euclide.
- Guardeño, A. J. (2000). L'eredità della matematica: da Euclide a Newton, i geni attraverso i loro libri. Università di Siviglia.



Nessun utente ha ancora commentato questo articolo.