Il teoria cinetica molecolare È uno che cerca di spiegare le osservazioni sperimentali dei gas da una prospettiva microscopica. Vale a dire, cerca di associare la natura e il comportamento delle particelle gassose, con le caratteristiche fisiche del gas come fluido; spiegare il macroscopico dal microscopico.
I gas sono sempre stati di interesse per gli scienziati a causa delle loro proprietà. Occupano l'intero volume del contenitore in cui si trovano, potendo essere completamente compressi senza che il loro contenuto opponga la minima resistenza; e se la temperatura aumenta, il contenitore inizia ad espandersi e può persino rompersi.
Molte di queste proprietà e comportamenti sono riassunti nelle leggi dei gas ideali. Tuttavia, considerano il gas nel suo insieme e non come un insieme di milioni di particelle sparse nello spazio; Inoltre, non fornisce, sulla base dei dati di pressione, volume e temperatura, ulteriori informazioni su come si muovono queste particelle.
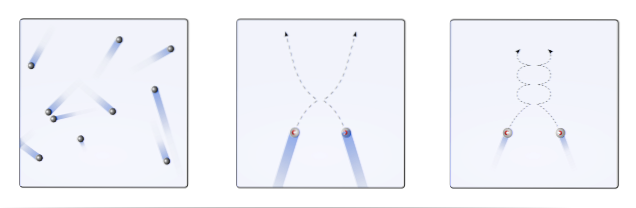
È quindi allora che la teoria cinetica molecolare (MTC), propone di visualizzarli come sfere mobili (immagine in alto). Queste sfere entrano in collisione tra loro e con le pareti in modo arbitrario e mantengono una traiettoria lineare. Tuttavia, quando la temperatura diminuisce e la pressione aumenta, la traiettoria delle sfere diventa curva..
Un gas, secondo TCM, dovrebbe comportarsi come le sfere nel primo fotogramma dell'immagine. Ma, raffreddandosi e aumentando la pressione su di loro, il loro comportamento è tutt'altro che ideale. Sono quindi dei veri gas, prossimi a subire la liquefazione e quindi passano alla fase liquida.
In queste condizioni, le interazioni tra le sfere diventano più importanti, al punto che le loro velocità rallentano momentaneamente. Più sono vicini alla liquefazione, più curve diventano le loro traiettorie (riquadro a destra) e meno energiche sono le loro collisioni.
Indice articolo
L'idea di queste sfere, meglio chiamate atomi, era già stata considerata dal filosofo romano Lucrezio; non per i gas, ma per oggetti solidi e statici. D'altra parte, nel 1738 Daniel Bernoulli applicò la visione atomica a gas e liquidi immaginandoli come sfere disordinate che si muovono in tutte le direzioni..
Il suo lavoro, tuttavia, violava le leggi della fisica dell'epoca; un corpo non poteva muoversi eternamente, quindi era impossibile pensare che un insieme di atomi e molecole si sarebbero scontrati tra loro senza perdere la loro energia; cioè, l'esistenza di collisioni elastiche non era possibile.
Un secolo dopo, altri autori hanno rafforzato la MTC con un modello in cui le particelle gassose si muovevano in una sola direzione. Rudolf Clausius, tuttavia, ha compilato i suoi risultati e messo insieme un modello TCM più completo con il quale ha cercato di spiegare le leggi dei gas ideali dimostrate da Boyle, Charles, Dalton e Avogadro..
Nel 1859, James Clerk Maxwell affermò che le particelle gassose mostrano un intervallo di velocità a una data temperatura e che un insieme di esse può essere considerato per mezzo di una velocità molecolare media..
Poi nel 1871 Ludwig Boltzmann collegò le idee esistenti con l'entropia, e come il gas termodinamicamente tende sempre ad occupare quanto più spazio possibile in modo omogeneo e spontaneo.
Per considerare il gas dalle sue particelle, è necessario un modello in cui siano soddisfatti determinati postulati o ipotesi; postulati che logicamente devono essere in grado di prevedere e spiegare (il più accuratamente possibile) osservazioni macroscopiche e sperimentali. Detto questo, vengono menzionati e descritti i postulati della MTC.
In un contenitore pieno di particelle gassose, queste si disperdono e si allontanano l'una dall'altra in tutti gli angoli. Se per un momento si potessero riunire tutti in un punto preciso del contenitore, senza liquefazione, si osserverebbe che occupano solo una porzione trascurabile del volume del contenitore..
Significa che il contenitore, anche se contiene milioni di particelle gassose, è in realtà più vuoto che pieno (rapporto volume-vuoti molto inferiore a 1); quindi, se le sue barriere lo consentono, esso e il gas al suo interno possono essere compressi bruscamente; poiché alla fine della giornata le particelle sono molto piccole, così come il loro volume.
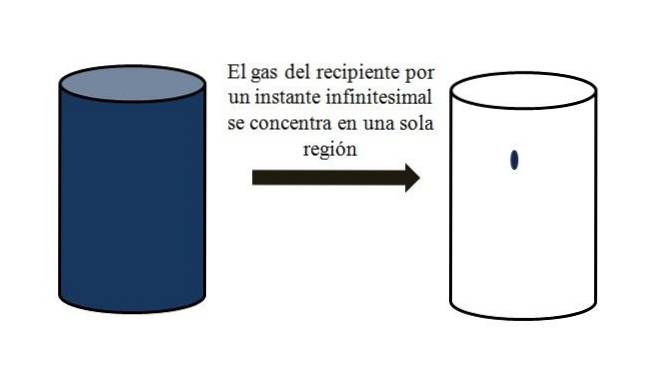
L'immagine in alto illustra accuratamente quanto sopra, utilizzando un gas di colore bluastro.
Le particelle gassose all'interno del contenitore si scontrano tra loro senza che le loro interazioni acquisiscano forza; ancor meno quando ciò che principalmente li circonda è il vuoto molecolare. Una conseguenza immediata di ciò è che i loro percorsi lineari consentono loro di inglobare completamente il volume del contenitore..
Se così non fosse, un contenitore di forma "bizzarra" e "labirintica" avrebbe delle zone umide per effetto della condensazione dei gas; invece, le particelle viaggiano intorno al contenitore con piena libertà, senza che la forza delle loro interazioni le fermi.
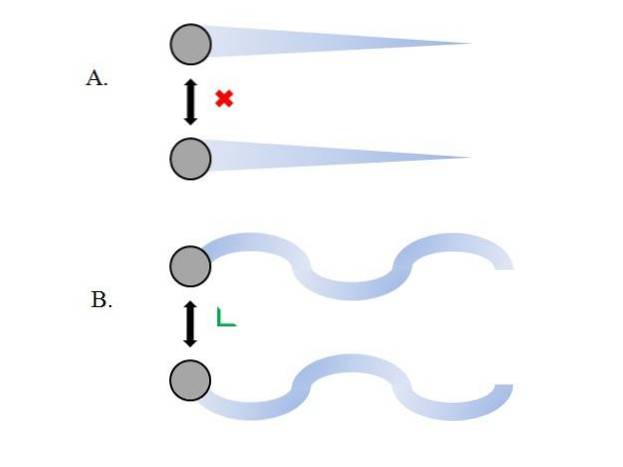
Le traiettorie lineari dell'immagine superiore (A.) dimostrano questo postulato; mentre se le traiettorie sono curve (B.), mostra che ci sono interazioni che non possono essere ignorate tra le particelle.
Dai primi due postulati converge anche il fatto che le particelle di gas non smettono mai di muoversi. Una volta sfumate nel contenitore, entrano in collisione tra loro e con le sue pareti, con una forza e una velocità direttamente proporzionali alla temperatura assoluta; questa forza è, pressione.
Se le particelle gassose smettessero di muoversi per un istante, si vedrebbero "lingue di fumo" all'interno del contenitore che emergono dal nulla, con tempo sufficiente per disporsi nel vuoto e dare forme casuali..
Se all'interno del contenitore predominano solo collisioni elastiche tra le particelle gassose e le pareti del contenitore, non si verificherà mai la condensazione del gas (purché le condizioni fisiche non cambino); o che cosa è come dire che non si fermano mai e si scontrano sempre.
Questo perché negli urti elastici non c'è perdita netta di energia cinetica; una particella si scontra con il muro e rimbalza alla stessa velocità. Se una particella in collisione rallenta, l'altra accelera, senza produrre calore o suono che dissipa l'energia cinetica di nessuna delle due.
Il movimento delle particelle è casuale e caotico, quindi non hanno tutte la stessa velocità; proprio come accade, ad esempio, in autostrada o in mezzo alla folla. Alcuni sono più energici e viaggiano più velocemente, mentre altri sono lenti, in attesa di una collisione per accelerarli.
Per descriverne la velocità è quindi necessario calcolare una media; e con ciò si ottiene a sua volta l'energia cinetica media delle particelle o molecole gassose. Poiché l'energia cinetica di tutte le particelle è in continua evoluzione, la media consente un miglior controllo dei dati e può essere lavorata con maggiore affidabilità..
Energia cinetica molecolare media (ECmp) in un contenitore cambia con la temperatura. Maggiore è la temperatura, maggiore sarà l'energia. Poiché è una media, potrebbero esserci particelle o gas che hanno un'energia maggiore o minore di questo valore; alcuni più veloci e altri più lenti, rispettivamente.
Matematicamente si può dimostrare che ECmp dipende esclusivamente dalla temperatura. Ciò significa che non importa quale sia il gas, la sua massa o struttura molecolare, la sua ECmp sarà lo stesso a una temperatura T e varierà solo se aumenta o diminuisce. Di tutti i postulati, questo è forse il più rilevante..
E la velocità molecolare media? A differenza di ECmp, la massa molecolare influenza la velocità. Più pesante è la particella o molecola gassosa, è naturale aspettarsi che si muova più lentamente..
Ecco alcuni brevi esempi di come la TCM è riuscita a spiegare le leggi dei gas ideali. Sebbene non affrontati, altri fenomeni, come la diffusione e l'effusione di gas, possono anche essere spiegati con la MTC.
Se il volume del contenitore viene compresso a temperatura costante, la distanza che le particelle gassose devono percorrere per entrare in collisione con le pareti diminuisce; che è uguale ad un aumento della frequenza di tali collisioni, con conseguente maggiore pressione. Poiché la temperatura rimane costante, ECmp è anche costante.
Se aumenti T, ECmp crescerà. Le particelle gassose si muoveranno più velocemente e collideranno un numero maggiore di volte con le pareti del contenitore; quindi la pressione aumenta.
Se le pareti sono flessibili, in grado di espandersi, la loro area diventerà più grande e la pressione diminuirà fino a diventare costante; e di conseguenza, anche il volume aumenterà.
Se in un contenitore capiente si aggiungessero più litri di gas diversi, provenienti da contenitori più piccoli, la sua pressione interna totale sarebbe pari alla somma delle pressioni parziali esercitate da ciascun tipo di gas separatamente..
Perché? Perché tutti i gas iniziano a entrare in collisione tra loro e a disperdersi in modo omogeneo; le interazioni tra loro sono nulle, e nel contenitore predomina il vuoto (postulati TCM), quindi è come se ogni gas fosse solo, esercitando la sua pressione singolarmente senza l'interferenza degli altri gas.
Nessun utente ha ancora commentato questo articolo.