Esempi di sequenze quadratiche, regole ed esercizi risolti

Il sequenze quadratiche, in termini matematici, sono costituiti da sequenze di numeri che seguono una certa regola aritmetica. È interessante conoscere questa regola per determinare uno qualsiasi dei termini di una sequenza.

Un modo per ottenere ciò è determinare la differenza tra due termini successivi e vedere se il valore ottenuto viene sempre ripetuto. Quando questo è il caso, si dice che sia un file successione regolare.

Ma se non viene ripetuto, puoi provare a esaminare il file differenza tra differenze e vedere se questo valore è costante. Se è così, allora è un file sequenza quadratica. 

Indice articolo

• 1 Esempi di sequenze regolari e sequenze quadratiche
  • 1.1 Esempio di successione regolare
  • 1.2 Esempio di successione non regolare e quadratica
• 2 Regola generale per costruire una successione quadratica
  • 2.1 Differenza tra due termini consecutivi di una successione quadratica
• 3 Risolti problemi di successioni quadratiche
  • 3.1 Esercizio 1
  • 3.2 Esercizio 2
  • 3.3 Esercizio 3
• 4 Riferimenti

Esempi di sequenze regolari e sequenze quadratiche

I seguenti esempi aiutano a chiarire cosa è stato spiegato finora:

Esempio di successione regolare

Lascia che la sequenza S = 4, 7, 10, 13, 16, ...

Questa sequenza, indicata con S, è un insieme numerico infinito, in questo caso di numeri interi.

Si può vedere che è una sequenza regolare, perché ogni termine si ottiene aggiungendo 3 al termine o elemento precedente:

4

4 +3 = 7

7+3 = 10

10+3 = 13

13+3 = 16

In altre parole: questa sequenza è regolare perché la differenza tra il termine successivo e quello precedente dà un valore fisso. Nell'esempio fornito questo valore è 3.

Vengono chiamate anche le sequenze regolari che si ottengono aggiungendo una quantità fissa al termine precedente progressioni aritmetiche. E si chiama la differenza -costante- tra termini successivi Motivo ed è indicato come R.

Esempio di successione non regolare e quadratica

Vedi ora la seguente sequenza:

S = 2, 6, 12, 20, 30,….

Quando vengono calcolate differenze successive, si ottengono i seguenti valori:

6-2 = 4

12-6 = 6

20-12 = 8

30-20 = 10

Le sue differenze non sono costanti, quindi si può dire che è una sequenza NON regolare.

Tuttavia, se consideriamo l'insieme delle differenze, abbiamo un'altra sequenza, che sarà indicata come S_diff:

S_diff = 4, 6, 8, 10,….

Questa nuova successione è a successione regolare, poiché ogni termine si ottiene sommando il valore fisso R = 2 a quello precedente. Quindi possiamo affermare che S è sequenza quadratica.

Regola generale per costruire una successione quadratica

C'è una formula generale per costruire una sequenza quadratica:

T_n = A ∙ n^Due + B ∙ n + C

In questa formula, T_n è il termine della posizione n della sequenza. A, B e C sono valori fissi, mentre n varia uno per uno, cioè 1, 2, 3, 4, ...

Nella sequenza S dell'esempio precedente A = 1, B = 1 e C = 0. Da lì ne consegue che la formula che genera tutti i termini è: T_n = n^Due + n

Vale a dire:

T₁ = 1^Due + 1 = 2

T_Due = 2^Due + 2 = 6

T₃ = 3^Due + 3 = 12

T₅ = 5^Due + 5 = 30

T_n = n^Due + n

Differenza tra due termini consecutivi di una successione quadratica

T_{n + 1} - T_n = [A ∙ (n + 1)^Due + B ∙ (n + 1) + C] - [A ∙ n^Due + B ∙ n + C]

Lo sviluppo dell'espressione attraverso un prodotto straordinario rimane:

T_{n + 1} - T_n = A ∙ n^Due + A ∙ 2 ∙ n + A + B ∙ n + B + C - A ∙ n^Due - B ∙ n - C

Semplificandolo, ottieni:

T_{n + 1} - T_n = 2 ∙ A ∙ n + A + B

Questa è la formula che dà la sequenza delle differenze S_Dif che può essere scritto in questo modo:

Dif_n = A ∙ (2n + 1) + B

Dove chiaramente il termine successivo è 2 ∙ A volte quello precedente. Cioè, il rapporto della sequenza delle differenze S_diff è: R = 2 ∙ A.

Risolti problemi di successioni quadratiche

Esercizio 1

Sia la sequenza S = 1, 3, 7, 13, 21,…. Determina se:

i) È regolare o no

ii) È quadratico o no

iii) Era quadratica, la sequenza delle differenze e il loro rapporto

Risposte

i) Calcoliamo la differenza tra i termini seguenti e quelli precedenti:

3-1 = 2

7-3 = 4

13-7 = 6

21-13 = 8

Possiamo affermarlo la sequenza S non è regolare, perché la differenza tra termini successivi non è costante.

ii) La sequenza delle differenze è regolare, perché la differenza tra i suoi termini è il valore costante 2. Quindi la sequenza originale S è quadratica.

iii) Abbiamo già determinato che S è quadratica, la sequenza delle differenze è:

S_diff = 2, 4, 6, 8, ... e il suo rapporto è R = 2.

Esercizio 2

Sia la successione S = 1, 3, 7, 13, 21,… dell'esempio precedente, dove si è verificato che è quadratica. Determinare:

i) La formula che determina il termine generale T_{n .}

ii) Verificare il terzo e il quinto termine.

iii) Il valore del decimo termine.

Risposte

i) La formula generale di T_n è A ∙ n^Due + B ∙ n + C. Quindi resta da conoscere i valori di A, B e C.

La sequenza delle differenze ha rapporto 2. Inoltre, per ogni sequenza quadratica il rapporto R è 2 ∙ A come mostrato nelle sezioni precedenti.

R = 2 ∙ A = 2 che ci porta a concludere che A = 1.

Il primo termine della sequenza delle differenze S_Dif è 2 e deve soddisfare A ∙ (2n + 1) + B, con n = 1 e A = 1, ovvero:

2 = 1 ∙ (2 ∙ 1 + 1) + B

risolvendo per B, otteniamo: B = -1

Allora il primo termine di S (n = 1) vale 1, cioè: 1 = A ∙ 1^Due + B ∙ 1 + C. Come già sappiamo che A = 1 e B = -1, sostituendo abbiamo:

1 = 1 ∙ 1^Due + (-1) ∙ 1 + C

Risolvendo per C otteniamo il suo valore: C = 1.

In sintesi:

A = 1, B = -1 e C = 1

Allora l'ennesimo termine sarà T_n = n^Due - n + 1

ii) Il terzo termine T₃ = 3^Due - 3 + 1 = 7 ed è verificato. La quinta T₅ = 5^Due - 5 + 1 = 21 che è anche verificato.

iii) Il decimo mandato sarà T₁₀ = 10^Due - 10 + 1 = 91.

Esercizio 3

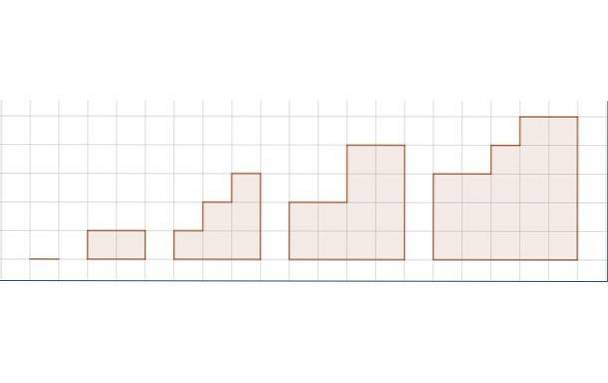
La figura mostra una sequenza di cinque figure. Il reticolo rappresenta l'unità di lunghezza.

i) Determina la sequenza per l'area delle figure.

ii) Mostra che è una successione quadratica.

iii) Trova l'area della figura # 10 (non mostrata).

Risposte

i) La sequenza S corrispondente all'area della sequenza di figure è:

S = 0, 2, 6, 12, 20,…

ii) La sequenza corrispondente alle differenze consecutive dei termini di S è:

S_diff = 2, 4, 6, 8,…

Poiché la differenza tra termini consecutivi non è costante, S non è una sequenza regolare. Resta da sapere se è quadratico, per cui rifacciamo la sequenza delle differenze, ottenendo:

2, 2, 2,….

Poiché tutti i termini della sequenza vengono ripetuti, si conferma che S è una sequenza quadratica.

iii) La sequenza S_diff è regolare e il suo rapporto R è 2. Usando l'equazione mostrata sopra R = 2 ∙ A, rimane:

2 = 2 ∙ A, il che implica che A = 1.

Il secondo termine della sequenza delle differenze S_Dif è 4 e l'ennesimo termine di S_Dif è

A ∙ (2n + 1) + B.

Il secondo termine ha n = 2. Inoltre, è già stato determinato che A = 1, quindi utilizzando l'equazione precedente e sostituendo, abbiamo:

4 = 1 ∙ (2 ∙ 2 + 1) + B

Risolvendo per B otteniamo: B = -1.

È noto che il secondo termine di S vale 2 e che deve soddisfare la formula del termine generale con n = 2:

T_n = A ∙ n^Due + B * n + C; n = 2; A = 1; B = -1; T_Due = 2

Vale a dire

2 = 1 ∙ 2^Due - 1 ∙ 2 + C

Si conclude che C = 0, vale a dire che la formula che dà il termine generale della successione S è:

T_n = 1 ∙ n^Due - 1 ∙ n +0 = n^Due - n

Ora il quinto termine è verificato:

T₅ = 5^Due - 5 = 20

iii) La figura # 10, che qui non è stata disegnata, avrà l'area corrispondente al decimo termine della sequenza S:

T₁₀ = 10^Due - 10 = 90

Riferimenti

1. https://www.geogebra.org