
Applicazioni, esperimenti ed esercizi della seconda legge di Newton
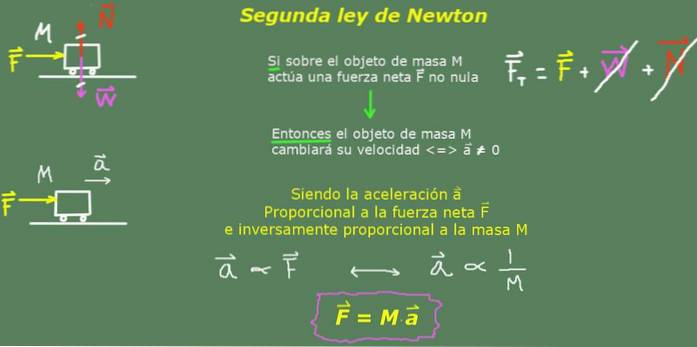
Il seconda legge di Newton oppure la legge fondamentale della dinamica stabilisce che se un oggetto è soggetto a una forza oa un insieme di forze che non si annullano, allora l'oggetto accelererà nella direzione della forza risultante, questa accelerazione essendo proporzionale all'intensità di quella forza netta e inversamente proporzionale alla massa dell'oggetto.
sì F è la forza netta, M la massa dell'oggetto e per l'accelerazione che acquisisce, quindi la seconda legge di Newton sarebbe espressa matematicamente in questo modo: per = F / M o nel modo più usuale F = M∙per
Indice articolo
- 1 Spiegazione e formule
- 2 Esercizi risolti
- 2.1 Esercizio 1
- 2.2 Esercizio 2
- 3 Applicazioni della seconda legge di Newton
- 3.1 L'accelerazione di un ascensore
- 3.2 Il barattolo di maionese
- 4 Esperimenti per bambini
- 4.1 Esperimento 1
- 4.2 Esperimento 2
- 5 Articoli di interesse
- 6 Riferimenti
Spiegazione e formule
Come spiegato sopra, il modo usuale per esprimere la seconda legge è con la formula:
F = M∙per
Sia l'accelerazione che la forza devono essere misurate da un sistema di riferimento inerziale. Nota che la massa è una quantità positiva, quindi l'accelerazione punta nella stessa direzione della forza risultante.
Nota anche che quando la forza risultante è zero (F = 0) allora anche l'accelerazione sarà zero ( per = 0 ) fintanto che M> 0. Questo risultato concorda pienamente con la prima legge o legge dell'inerzia di Newton.
La prima legge di Newton stabilisce i sistemi di riferimento inerziali come quelli che si muovono a velocità costante rispetto a una particella libera. In pratica e ai fini delle applicazioni più comuni, sarà considerato inerziale un sistema di riferimento fissato al suolo o qualsiasi altro che si muova a velocità costante rispetto ad esso..
La forza è l'espressione matematica dell'interazione dell'oggetto con l'ambiente. La forza può essere una quantità costante o cambiare nel tempo, la posizione e la velocità dell'oggetto..
L'unità nel Sistema Internazionale (SI) per la forza è il Newton (N). La massa in (SI) è misurata in (kg) e l'accelerazione in (m / sDue). Un Newton di forza è la forza necessaria per accelerare un oggetto di massa 1 kg a 1 m / sDue .
Esercizi risolti
Esercizio 1
Un oggetto di massa m viene rilasciato da una certa altezza e viene misurata un'accelerazione di caduta di 9,8 m / s².
Lo stesso accade con un altro oggetto di massa m 'e un altro di massa m "e un altro e un altro. Il risultato è sempre l'accelerazione di gravità che è indicata con g ed è pari a 9,8 m / s². In questi esperimenti la forma del oggetto e il valore della sua massa è tale che la forza dovuta alla resistenza dell'aria è trascurabile.
Viene chiesto di trovare un modello per la forza di attrazione della terra (nota come peso) che sia coerente con i risultati sperimentali..
Soluzione
Scegliamo un sistema di riferimento inerziale (fisso rispetto al suolo) con direzione positiva dell'asse X verticale e verso il basso.
L'unica forza che agisce sull'oggetto massa m è l'attrazione della terra, quella forza si chiama peso P, il modo in cui punta verso il basso è positivo.
L'accelerazione che acquisisce l'oggetto massa m una volta rilasciato lo è a = g , puntato verso il basso e positivo.
Proponiamo la seconda legge di Newton
P = m a
Quale sarà il modello di P tale che l'accelerazione prevista dalla seconda legge sia g indipendentemente dal valore di m? : L'unica alternativa è che P = m g ogni volta che m> 0.
m g = m a da dove si cancella: a = g
Concludiamo che il peso, la forza con cui la Terra attrae un oggetto sarà la massa dell'oggetto moltiplicata per l'accelerazione di gravità e la sua direzione è verticale e puntata verso il basso.
P = m∙g
Esercizio 2
Un blocco di 2 kg di massa poggia su un pavimento completamente piatto e orizzontale. Se gli viene applicata una forza di 1 N, qual è l'accelerazione del blocco e quale velocità avrà dopo 1 s.
Soluzione
La prima cosa è definire un sistema di coordinate inerziali. Uno è stato scelto con l'asse X sul pavimento e l'asse Y perpendicolare ad esso. Quindi viene creato un diagramma delle forze, posizionando le forze dovute alle interazioni del blocco con il suo ambiente.

La forza N rappresenta la normale, è la forza verticale verso l'alto che la superficie del pavimento esercita sul blocco M. È noto che N equilibra esattamente P perché il blocco non si muove in direzione verticale.
F è la forza orizzontale applicata al blocco M, che punta nella direzione positiva dell'asse X..
La forza netta è la somma di tutte le forze sul blocco di massa M. Facciamo la somma vettoriale di F, P e N. Poiché P e N sono uguali e opposti, si annullano a vicenda e la forza netta è F.
Quindi l'accelerazione risultante sarà il quoziente della forza netta e della massa:
a = F / M = 1 N / 2 kg = 0,5 m / s²
Poiché il blocco parte da fermo dopo 1 secondo, la sua velocità sarà cambiata da 0 m / sa 0,5 m / s .
Applicazioni della seconda legge di Newton
Accelerare un ascensore
Un ragazzo usa una bilancia da bagno per misurare il suo peso. Il valore che ottieni è di 50 kg. Quindi il ragazzo porta il peso all'ascensore del suo edificio, perché vuole misurare l'accelerazione dell'ascensore. I risultati ottenuti all'avvio sono:
- La bilancia registra un peso di 58 kg per 1,5 s
- Quindi misurare di nuovo 50 kg.
Con questi dati, calcola l'accelerazione dell'ascensore e la velocità che acquisisce.
Soluzione
La bilancia misura il peso in un'unità chiamata kilogram_force. Per definizione, il kilogram_force è la forza con cui il pianeta Terra attrae un oggetto di massa 1 kg.
Quando l'unica forza che agisce sull'oggetto è il suo peso, acquisisce un'accelerazione di 9,8 m / s². Quindi 1 kg_f è uguale a 9,8 N.
Il peso P del ragazzo è quindi 50 kg * 9,8 m / s² = 490 N
Durante l'accelerazione la bilancia esercita una forza N sul ragazzo di 58 kg_f equivalente a 58 kg * 9,8 m / s² = 568,4 N.
L'accelerazione dell'ascensore sarà data da:
a = N / M - g = 568,4 N / 50 kg - 9,8 m / s² = 1,57 m / s²
La velocità acquisita dall'ascensore dopo 1,5 s con accelerazione di 1,57 m / s² è:
v = a * t = 1,57 m / s² * 1,5 s = 2,36 m / s = 8,5 Km / h
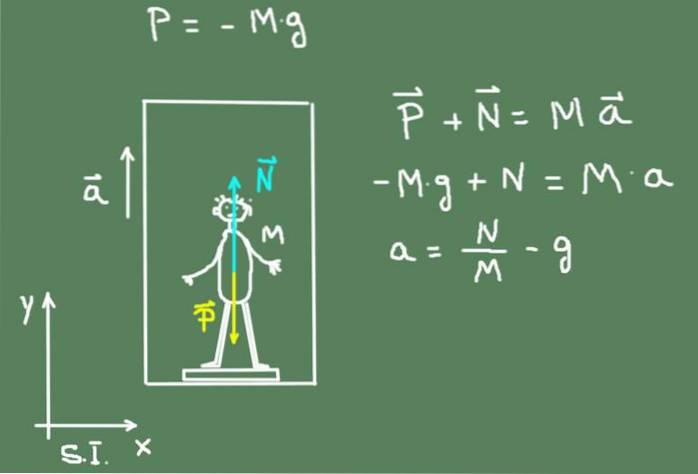
La figura seguente mostra un diagramma delle forze che agiscono sul ragazzo:
Il barattolo di maionese
Un ragazzo porge a suo fratello il barattolo di maionese a suo fratello, che è all'altro capo del tavolo. Per questo, lo guida in modo tale da acquisire una velocità di 3 m / s. Dal momento in cui la bottiglia è stata rilasciata fino a quando non si è fermata all'estremità opposta del tavolo, la corsa è stata di 1,5 m.
Determina il valore della forza di attrito che il tavolo esercita sulla bottiglia, sapendo che ha una massa di 0,45 kg.
Soluzione
Per prima cosa determineremo l'accelerazione in frenata. Per questo utilizzeremo la seguente relazione, già nota dal moto rettilineo uniformemente accelerato:
Vf² = Vi² + 2 * a * d
dove Vf è la velocità finale, Sega velocità iniziale, per accelerazione e d lo spostamento.
L'accelerazione ottenuta dalla relazione precedente è, dove lo spostamento della bottiglia è stato considerato positivo.
a = (0-9 (m / s) ²) / (2 * 1,5 m) = -3 m / s²
La forza netta sul barattolo di maionese è la forza di attrito, poiché il normale e il peso del barattolo si bilanciano: Fnet = Fr.
Fr = m * a = 0,45 kg * (-3 m / s²) = -1,35 N = -0,14 kg-f
Esperimenti per bambini
Bambini e adulti possono eseguire semplici esperimenti che consentono loro di verificare che la seconda legge di Newton funziona davvero nella vita reale. Eccone due molto interessanti:
Esperimento 1
Un semplice esperimento richiede una bilancia pesapersone e un ascensore. Porta un peso da bagno in un ascensore e registra i valori che segna durante la partenza in salita, la partenza in discesa e durante il tempo in cui ti muovi a velocità costante. Calcola le accelerazioni dell'ascensore per ogni caso.
Esperimento 2
- Prendi una macchinina con le ruote ben lubrificate
- Attacca una corda all'estremità.
- Sul bordo del tavolo, fissa una matita o un altro oggetto cilindrico liscio su cui passerà lo spago..
- All'altra estremità della corda, appendi un piccolo cestino, a cui appoggerai alcune monete o qualcosa che funga da peso..
Lo schema dell'esperimento è mostrato di seguito:
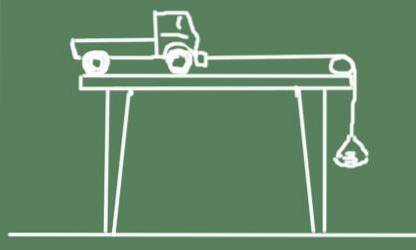
- Lascia cadere il carrello e guardalo accelerare.
- Quindi aumenta la massa del carrello posizionandovi sopra delle monete o qualcosa che ne aumenti la massa..
- Dire se l'accelerazione aumenta o diminuisce. Metti più pasta sul carrello, guardalo accelerare e finisci.
Il carrello viene quindi lasciato senza peso aggiuntivo e consentito di accelerare. Viene quindi posto più peso sul cestello per aumentare la forza applicata al carrello..
- Confronta l'accelerazione con il caso precedente, indica se aumenta o diminuisce. Puoi ripetere l'aggiunta di più peso al carrello e osservare l'accelerazione del carrello.
- Indicare se aumenta o diminuisce.
- Analizza i tuoi risultati e dì se sono d'accordo o meno con la seconda legge di Newton.
Articoli di interesse
Esempi della seconda legge di Newton.
La prima legge di Newton.
Esempi della seconda legge di Newton.
Riferimenti
- Alonso M., Finn E. 1970. Physics volume I: Mechanics. Fondo interamericano per l'educazione S.A. 156-163.
- Hewitt, P. 2012. Scienze fisiche concettuali. Quinta edizione. 41-46.
- Giovane, Hugh. 2015. Fisica universitaria con fisica moderna. 14 ° Ed. Pearson. 108-115.

Nessun utente ha ancora commentato questo articolo.