Il relazione matematica è il legame che esiste tra gli elementi di un sottoinsieme rispetto al prodotto di due insiemi. UN funzione implica l'operazione matematica per determinare il valore di una variabile dipendente in base al valore di una variabile indipendente. Ogni funzione è una relazione, ma non tutte le relazioni sono una funzione.
| Relazione | Funzione | |
|---|---|---|
| Definizione | Sottoinsieme di coppie ordinate che corrispondono al prodotto cartesiano di due insiemi. | Operazione matematica da eseguire con la variabile X per ottenere la variabile Y. |
| Notazione | X R Y; X è correlato a Y. | Y= ƒ (X); Y è una funzione di X. |
| Caratteristiche |
|
|
| Esempi |
|
|
Si chiama relazione binaria di un insieme A in un insieme B o relazione tra elementi di A e B con ogni sottoinsieme C del prodotto cartesiano A x B.
Cioè, se l'insieme A è composto dagli elementi 1, 2 e 3 e l'insieme B è composto dagli elementi 4 e 5, il prodotto cartesiano di A x B saranno le coppie ordinate:
A x B = (1,4), (2,4), (3, 4), (1,5), (2,5), (3,5).
Il sottoinsieme C = (2,4), (3,5) sarà una relazione di A e B poiché è composto dalle coppie ordinate (2,4) e (3, 5), il risultato del cartesiano prodotto di A x B.
"Siano A e B due insiemi non vuoti, A x B sia l'insieme di prodotti di entrambi, cioè: A x B è formato dalle coppie ordinate (x, y) tali che X è l'elemento di A e Y è per B. Se un qualsiasi sottoinsieme C è definito in A x B, una relazione binaria in A e B viene determinata automaticamente come segue:
X R Y se e solo se (x, y) ∈ C
(la notazione X R Y Si intende "X è correlato a Y").
Chiameremo set A set di partenza e chiameremo set B arrivo impostato.
Il dominio di relazione sono gli elementi che compongono il set di partenza, mentre il gamma di rapporti sono gli elementi del set di arrivo.
Impostato PER a partire dal X elementi di uomini in una popolazione e B è l'insieme di Y elementi di donne della stessa popolazione. Viene stabilita una relazione quando "X è sposato con Y".
Quando parliamo di una funzione matematica di un insieme A in un insieme B ci riferiamo a una regola o meccanismo che mette in relazione gli elementi dell'insieme A con un elemento dell'insieme B.
"Sean X Y Y due variabili reali, si dice poi che y è una funzione di x sì a ogni valore che prendo X corrisponde a un valore di Y."
La variabile indipendente è X mentre Y è la variabile o la funzione dipendente:
y = ƒ (x)
Il set in cui il X è chiamato dominio della funzione (originale) e la variazione di Y gamma di funzioni (immagine).
L'insieme delle coppie (X, Y) tale che Y= ƒ (X) è chiamato grafico delle funzioni; se sono rappresentati in assi cartesiani, si ottiene una famiglia di punti denominata grafico delle funzioni.
In matematica otteniamo molti esempi di funzioni. Ecco alcuni esempi di funzioni di punta.
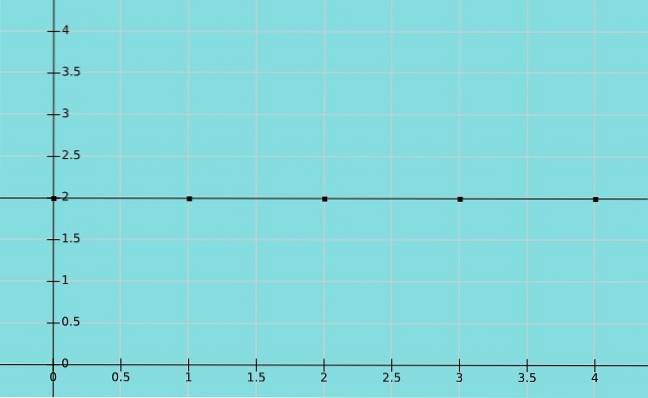
Una funzione è chiamata costante se l'elemento dell'insieme B che corrisponde all'insieme A è lo stesso. In questo caso, tutti i valori di x corrispondono allo stesso valore di y. Pertanto, il dominio è i numeri reali mentre l'intervallo è un valore costante.
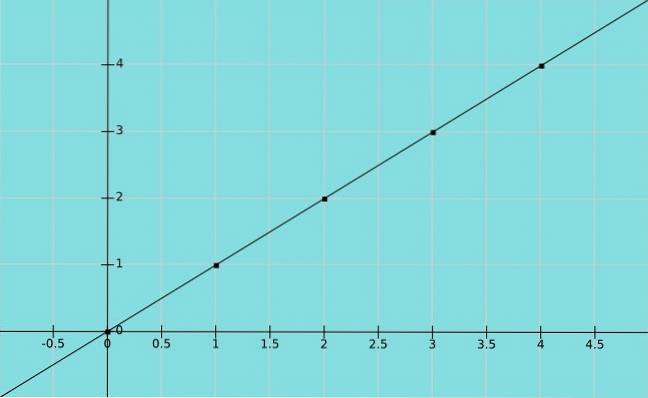
Supponiamo X è una variabile e quella Y assume lo stesso valore di X. Abbiamo quindi una funzione di identità y = x, dove le coppiex, y) nel grafico sono (1,1), (2,2), (3,3) e così via.
Una funzione polinomiale soddisfa la forma y = anXn+pern-1+Xn-1+... + ADueXDue+per1x + a0. Il grafico sopra mostra la funzione ƒ (x) = xDue+x-2.
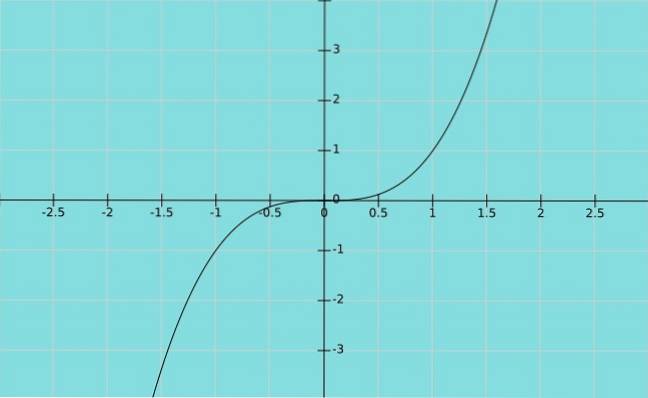
Supponiamo ora che la variabile dipendente Y è uguale alla variabile indipendente X elevato al cubo. Abbiamo la funzione y = x3, il cui grafico è mostrato di seguito:
Nessun utente ha ancora commentato questo articolo.