Qual è il modulo di taglio, rigidità o taglio? (Esercizi risolti)

Il modulo di taglio descrive la risposta di un materiale all'applicazione di uno sforzo di taglio che lo deforma. Altri nomi usati di frequente per modulo di taglio sono modulo di taglio, modulo di taglio, elasticità trasversale o elasticità tangenziale..

Quando le sollecitazioni sono piccole, le deformazioni sono ad esse proporzionali, secondo la legge di Hooke, essendo il modulo di taglio la costante di proporzionalità. Perciò:

Modulo di taglio = Sforzo di taglio / Deformazione

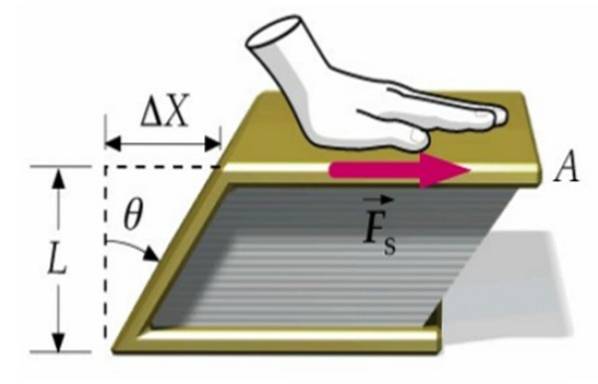
Supponiamo che una forza venga applicata alla copertina di un libro e che l'altra sia fissata sulla superficie del tavolo. In questo modo, il libro nel suo insieme non si muove, ma si deforma quando la copertina superiore si sposta rispetto a quella inferiore della quantità Δx.

Il libro passa dall'avere una sezione trasversale rettangolare ad una sezione a forma di parallelogramma, come vediamo nell'immagine sopra.

Essere:

τ = F / A

Lo sforzo di taglio o tensione, essere F l'entità della forza applicata e PER l'area su cui agisce.

La deformazione provocata è data dal quoziente:

δ = Δx / L

Pertanto il modulo di taglio, che indicheremo con G, è:

E poiché Δx / L non ha dimensioni, le unità di G sono le stesse dello sforzo di taglio, che è il rapporto tra forza e area..

Nel Sistema internazionale di unità, queste unità sono Newton / metro quadro o pascal, abbreviato Pa. E nelle unità anglosassoni è libbra / pollice quadrato, abbreviato psi.

Indice articolo

• 1 Modulo di taglio per vari materiali
  • 1.1 Misura sperimentale del modulo di taglio
  • 1.2 Come trovare G?
• 2 Esercizi con soluzione
  • 2.1 - Esercizio 1
  • 2.2 - Esercizio 2
• 3 Riferimenti

Modulo di taglio per vari materiali

Sotto l'azione di forze di taglio come quelle descritte, gli oggetti offrono una resistenza simile a quella del libro, in cui scorrono gli strati interni. Questo tipo di deformazione può verificarsi solo in corpi solidi, che hanno una rigidità sufficiente per resistere alla deformazione..

I liquidi invece non offrono questo tipo di resistenza, ma possono subire deformazioni di volume.

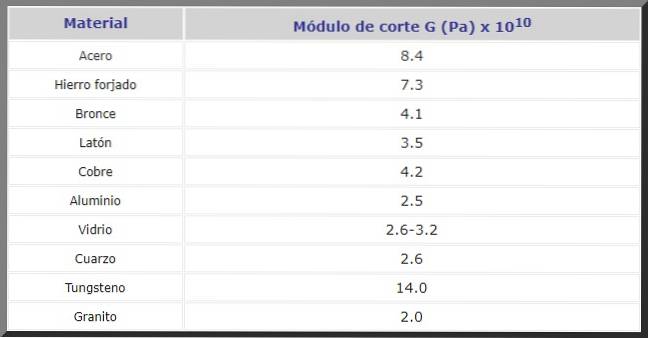
Di seguito il modulo di taglio G in Pa per vari materiali frequentemente utilizzati nell'edilizia e nella fabbricazione di macchinari e ricambi di ogni genere:

Misura sperimentale del modulo di taglio

Per trovare il valore del modulo di taglio, è necessario testare campioni di ciascun materiale e esaminare la loro risposta all'applicazione di uno sforzo di taglio..

Il campione è un'asta realizzata con il materiale, con raggio R e lunghezza L nota, che è fissata ad un'estremità, mentre l'altra è collegata all'albero di una puleggia libera di ruotare.

La carrucola è legata con una corda, all'estremità libera della quale è appeso un peso che esercita una forza F sull'asta attraverso la corda. E questa forza a sua volta produce un momento M sull'asta, che poi ruota di un piccolo angolo θ.

Uno schema dell'assieme può essere visto nella figura seguente:

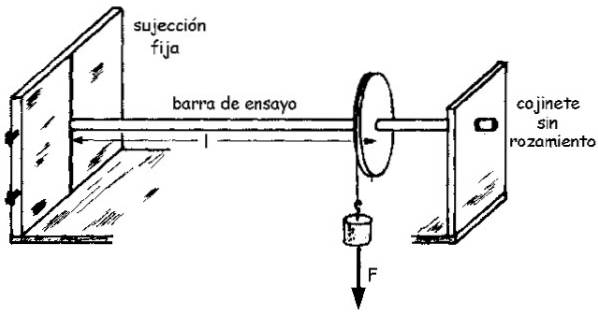
La grandezza del momento M, che indichiamo come M (no grassetto) è correlato all'angolo ruotato θ attraverso il modulo di taglio G secondo la seguente equazione (dedotta da un integrale semplice):

Poiché l'entità del momento è uguale al prodotto del modulo della forza F e del raggio della puleggia R_p:

M = F.R_p

E la forza è il peso che pende W, poi:

M = W.R_p

Sostituendo nell'equazione la grandezza del momento:

C'è la relazione tra peso e angolo:

Come trovare G?

Questa relazione tra le variabili W Y θ è lineare, quindi vengono misurati i diversi angoli prodotti dall'attaccatura di pesi diversi.

Le coppie di peso e angolo vengono tracciate su carta millimetrata, viene adattata la linea migliore che passa attraverso i punti sperimentali e viene calcolata la pendenza. m di detta linea.

Esercizi con soluzione

- Esercizio 1

Ad un'estremità è fissata un'asta di 2,5 metri di lunghezza e 4,5 mm di raggio. L'altro è collegato ad una carrucola con raggio di 75 cm che ha un peso sospeso W di 1,3 kg. L'angolo ruotato è di 9,5º.

Con questi dati si richiede di calcolare il modulo di taglio G dello stelo.

Soluzione

Dall'equazione:

G è cancellato:

E i valori riportati nella dichiarazione vengono sostituiti, avendo cura di esprimere tutti i dati nel Sistema Internazionale di Unità SI:

R = 4,5 mm = 4,5 x 10 ^-3 m

R_p = 75 cm = 0,075

Per passare da chilogrammi (che in realtà sono chilogrammi - forza) a newton moltiplicare per 9,8:

W = 1,3 kg-forza = 1,3 x 9,8 N = 12,74 N

Infine, i gradi devono essere in radianti:

9,5 º = 9,5 x2π / 360 radianti = 0,1658 radianti.

Con tutto questo hai:

= 2.237 x 10¹⁰ papà

- Esercizio 2

Un cubo di gel ha un lato di 30 cm. Una delle sue facce è fissa, ma allo stesso tempo viene applicata una forza parallela di 1 N alla faccia opposta, che grazie ad essa si sposta di 1 cm (vedi esempio del libro in figura 1).

Si richiede di calcolare con questi dati:

a) L'entità dello sforzo di taglio

b) Filtrare δ

c) Il valore del modulo di taglio

Soluzione a

L'entità dello sforzo di taglio è:

τ = F / A

Con:

A = lato^Due = (30 x 10^-Due cm)^Due = 0,09 m^Due

Perciò:

τ = 1 N / 0,09 m^Due = 11,1 Pa

Soluzione b

La deformazione non è altro che il valore di δ, dato da:

δ = Δx / L

Lo spostamento del viso sottoposto alla forza è di 1 cm, quindi:

δ = 1/30 = 0,0333

Soluzione c

Il modulo di taglio è il quoziente tra lo sforzo di taglio e la deformazione:

G = sforzo di taglio / deformazione

Perciò:

G = 11,1 Pa / 0,033 = 336,4 Pa

Riferimenti

1. Beer, F. 2010. Meccanica dei materiali. McGraw Hill. 5 °. Edizione.
2. Franco García, A. Solid Rigid. Misura del modulo di taglio. Recupero da: sc.ehu.es.
3. Giancoli, D. 2006. Fisica: principi con applicazioni. 6 °. Ed prentice hall.
4. Resnick, R. (1999). Fisico. Vol. 1. 3a Ed. In spagnolo. Azienda editoriale Continental S.A. di C.V.
5. Università di Valladolid. Dipartimento di Fisica della Materia Condensata. Selezione dei problemi. Estratto da: www4.uva.es.