
Proprietà di blocco della prova algebrica, esempi
Il proprietà lock dell'algebra è un fenomeno che mette in relazione due elementi di un insieme con un'operazione, dove la condizione necessaria è che, dopo che i 2 elementi sono stati elaborati sotto detta operazione, il risultato appartenga anche all'insieme iniziale.
Ad esempio, se i numeri pari sono presi come un insieme e una somma come un'operazione, si ottiene un blocco di quell'insieme rispetto alla somma. Questo perché la somma di 2 numeri pari produrrà sempre un altro numero pari, soddisfacendo così la condizione di blocco.

Indice articolo
- 1 Caratteristiche
- 2 Algebra dei numeri
- 3 Demo
- 3.1 Somma
- 3.2 Moltiplicazione
- 4 Casi speciali in R
- 4.1 Divisione
- 4.2 Archiviazione
- 4.3 Logaritmo
- 5 esempi
- 5.1 Somma in N
- 5.2 Sottrazione in N
- 6 Esercizi proposti
- 7 Riferimenti
Caratteristiche
Esistono molte proprietà che determinano spazi o corpi algebrici, come strutture o anelli. Tuttavia, la proprietà lock è una delle più conosciute all'interno dell'algebra di base.
Non tutte le applicazioni di queste proprietà si basano su elementi o fenomeni numerici. Molti esempi quotidiani possono essere elaborati da un puro approccio algebrico-teorico.
Un esempio possono essere i cittadini di un paese che assumono una relazione legale di qualsiasi tipo, come una partnership commerciale o un matrimonio tra gli altri. Dopo questa operazione o gestione, rimangono cittadini del paese. In questo modo le operazioni di cittadinanza e gestione nei confronti di due cittadini rappresentano una serratura.
Algebra numerica
Per quanto riguarda i numeri, sono molti gli aspetti che sono stati oggetto di studio in diverse correnti di matematica e algebra. Da questi studi è emerso un gran numero di assiomi e teoremi che servono come base teorica per la ricerca e il lavoro contemporanei..
Se lavoriamo con gli insiemi numerici possiamo stabilire un'altra definizione valida per la proprietà lock. Si dice che un insieme A sia il blocco di un altro insieme B se A è l'insieme più piccolo che contiene tutti gli insiemi e le operazioni che B ospita..
Dimostrazione
La prova di blocco si applica agli elementi e alle operazioni presenti nell'insieme dei numeri reali R.
Siano A e B due numeri che appartengono all'insieme R, la chiusura di questi elementi è definita per ogni operazione contenuta in R.
Somma
- Somma: ∀ A ˄ B ∈ R → A + B = C ∈ R
Questo è il modo algebrico per dirlo Per tutti A e B che appartengono ai numeri reali, abbiamo che la somma di A più B è uguale a C, che appartiene anche ai numeri reali.
È facile verificare se questa proposizione è vera; è sufficiente effettuare la somma tra un qualsiasi numero reale e verificare se il risultato appartiene anche ai numeri reali.
3 + 2 = 5 ∈ R
-2 + (-7) = -9 ∈ R
-3 + 1/3 = -8/3 ∈ R
5/2 + (-2/3) = 11/6 ∈ R
Si osserva che la condizione di blocco è soddisfatta per i numeri reali e la somma. In questo modo si può concludere: La somma dei numeri reali è un blocco algebrico.
Moltiplicazione
- Moltiplicazione: ∀ A ˄ B ∈ R → A. B = C ∈ R
Per tutti A e B che appartengono ai reali, abbiamo che la moltiplicazione di A per B è uguale a C, che appartiene anche ai reali.
Durante la verifica con gli stessi elementi dell'esempio precedente, si osservano i seguenti risultati.
3 x 2 = 6 ∈ R
-2 x (-7) = 14 ∈ R
-3 x 1/3 = -1 ∈ R
5/2 x (-2/3) = -5/3 ∈ R
Questa è una prova sufficiente per concludere che: La moltiplicazione dei numeri reali è un blocco algebrico.
Questa definizione può essere estesa a tutte le operazioni sui numeri reali, anche se troveremo alcune eccezioni.

Casi speciali in R
Divisione
Come primo caso speciale, si osserva la divisione, dove si osserva la seguente eccezione:
∀ LA ˄ B ∈ R → A / B ∉ R ↔ B = 0
Per tutti A e B che appartengono a R abbiamo che A tra B non appartiene ai reali se e solo se B è uguale a zero.
Questo caso si riferisce alla restrizione di non poter dividere per zero. Poiché zero appartiene ai numeri reali, si conclude che: lLa divisione non è un blocco sui reali.
Archiviazione
Esistono anche operazioni di potenziamento, più specificamente quelle di radicalizzazione, dove vengono presentate eccezioni per poteri radicali di pari indice:
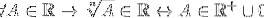
Per ogni A che appartiene ai reali, l'ennesima radice di A appartiene ai reali, se e solo se A appartiene ai reali positivi uniti a un insieme il cui unico elemento è zero.
In questo modo si denota che le radici pari si applicano solo a reali positivi e si conclude che il potenziamento non è un blocco in R.
Logaritmo
In maniera omologa si può vedere per la funzione logaritmica, che non è definita per valori minori o uguali a zero. Per verificare se il logaritmo è un blocco di R, procedere come segue:
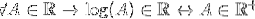
Per ogni A che appartiene ai reali, il logaritmo di A appartiene ai reali, se e solo se A appartiene ai reali positivi.
Escludendo valori negativi e zero che appartengono anche a R, si può affermare che:
Il logaritmo non è un blocco dei numeri reali.
Esempi
Controlla il blocco per l'addizione e la sottrazione di numeri naturali:
Somma in N
La prima cosa è controllare la condizione di blocco per diversi elementi dell'insieme dato, dove se si osserva che qualsiasi elemento rompe con la condizione, l'esistenza di un blocco può essere automaticamente negata.
Questa proprietà è vera per tutti i possibili valori di A e B, come osservato nelle seguenti operazioni:
1 + 3 = 4 ∈ N
5 + 7 = 12 ∈ N
1000 + 10000 = 11000 ∈ N
Non ci sono valori naturali che rompono la condizione di blocco, quindi si conclude:
La somma è una serratura in N.
Sottrai in N
Sono alla ricerca di elementi naturali in grado di rompere la condizione; A - B appartiene ai nativi.
Operando è facile trovare coppie di elementi naturali che non soddisfano la condizione di blocco. Per esempio:
7-10 = -3 ∉ a N
In questo modo possiamo concludere che:
La sottrazione non è un blocco dell'insieme dei numeri naturali.
Esercizi proposti
1-Mostra se la proprietà lock è soddisfatta per l'insieme di numeri razionali Q, per le operazioni di addizione, sottrazione, moltiplicazione e divisione.
2-Spiega se l'insieme di numeri reali è un blocco dell'insieme di numeri interi.
3-Determina quale set numerico può essere bloccato sui numeri reali.
4-Dimostrare la proprietà di blocco per l'insieme di numeri immaginari, rispetto a addizione, sottrazione, moltiplicazione e divisione.
Riferimenti
- Panorama di matematica pura: la scelta bourbakista. Jean Dieudonné. Reverte, 1987.
- Teoria algebrica dei numeri. Alejandro J. Díaz Barriga, Ana Irene Ramírez, Francisco Tomás. Università Nazionale Autonoma del Messico, 1975.
- Algebra lineare e sue applicazioni. Sandra Ibeth Ochoa García, Eduardo Gutiérrez González.
- Strutture algebriche V: teoria del corpo. Hector A. Merklen. Organizzazione degli Stati americani, Segretariato generale, 1979.
- Introduzione all'algebra commutativa. Michael Francis Atiyah, I. G. MacDonald. Reverte, 1973.



Nessun utente ha ancora commentato questo articolo.