In un processo isobarico, la pressione P di un sistema rimane costante. Il prefisso "iso" viene dal greco ed è usato per denotare che qualcosa rimane costante, mentre "baros", anche dal greco, significa peso.
I processi isobarici sono molto tipici sia nei contenitori chiusi che negli spazi aperti, essendo facilmente individuabili in natura. Con questo si intende che sono possibili cambiamenti fisici e chimici sulla superficie terrestre o reazioni chimiche in contenitori aperti all'atmosfera..
Alcuni esempi si ottengono riscaldando un palloncino riempito d'aria al sole, cuocendo, facendo bollire o congelando acqua, vapore generato nelle caldaie, o il processo di sollevamento di una mongolfiera. Successivamente daremo una spiegazione di questi casi.
Indice articolo
Deriviamo un'equazione per il processo isobarico assumendo che il sistema in esame sia un gas ideale, un modello abbastanza adatto per quasi tutti i gas a meno di 3 atmosfere di pressione. Le particelle di gas ideale si muovono in modo casuale, occupando l'intero volume dello spazio che le contiene senza interagire tra loro..
Se si lascia espandere lentamente il gas ideale racchiuso in un cilindro dotato di pistone mobile, si può presumere che le sue particelle siano sempre in equilibrio. Quindi il gas esercita sul pistone di area PER una forza F di grandezza:
F = p.A
Dove p è la pressione del gas. Questa forza esercita un lavoro producendo uno spostamento infinitesimale dx sul pistone dato da:
dW = Fdx = pA.dx
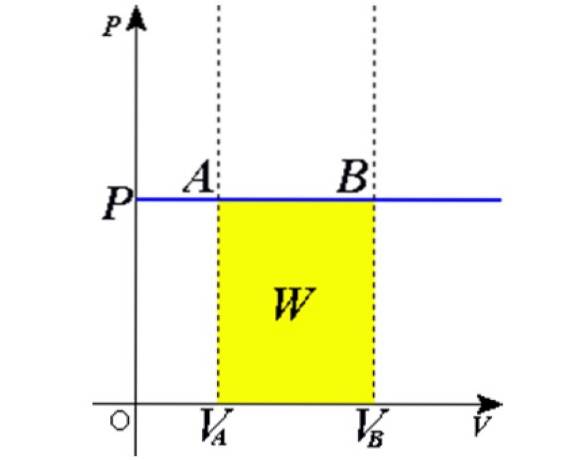
Come il prodotto Adx è un differenziale di volume dV, poi dW = pdV. Resta da integrare entrambi i lati dal volume iniziale VPER fino al volume finale VB per ottenere il lavoro totale svolto dal gas:
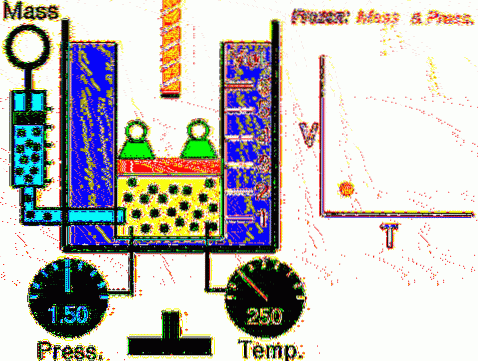
La situazione descritta viene verificata sperimentalmente confinando un gas all'interno di una bombola provvista di pistone mobile, come mostrato nelle figure 2 e 3. Sul pistone viene posto un peso di massa M, il cui peso è diretto verso il basso, mentre il gas esercita una forza verso l'alto grazie alla pressione P prodotta sul pistone.
Poiché il pistone è in grado di muoversi liberamente, il volume che occupa il gas può cambiare senza problemi, ma la pressione rimane costante. Sommando la pressione atmosferica PATM, che esercita anche una forza verso il basso, abbiamo:
Mg - P.A + PATM . A = costante
Quindi: P = (Mg / A) + PATM non varia, a meno che M e quindi il peso non vengano modificati. Aggiungendo calore alla bombola, il gas si espanderà aumentando il suo volume o si contrarrà durante l'estrazione del calore..
L'equazione di stato dei gas ideali mette in relazione le variabili di importanza: pressione P, volume V e temperatura T:
P.V = n .R.T
Qui n rappresenta il numero di moli e R è la costante del gas ideale (valida per tutti i gas), che viene calcolata moltiplicando la costante di Boltzmann per il numero di Avogadro, ottenendo:
R = 8,31 J / mol K
Quando la pressione è costante, l'equazione di stato può essere scritta come:
V / T = nR / P
Ma nR / P è costante, poiché n, R e P lo sono. Quindi, quando il sistema passa dallo stato 1 allo stato 2, si verifica la seguente proporzione, nota anche come legge di Charles:
V1/ T1 = VDue/ TDue
Sostituzione in W = PΔV, il lavoro svolto per passare dallo stato 1 allo stato 2 si ottiene, in termini di costanti e variazione di temperatura, facilmente misurabile con un termometro:
W1 → 2 = nR (TDue - T1) = nR.ΔT
D'altra parte, la prima legge della termodinamica afferma che:
∆U = Q - W
Ciò significa che l'aggiunta di una certa quantità di calore Q al gas aumenta l'energia interna ∆U e aumenta le vibrazioni delle sue molecole. In questo modo il gas si espande e funziona muovendo il pistone, come abbiamo detto prima..
In un gas ideale monoatomico e la variazione dell'energia interna ∆U, che include sia l'energia cinetica che l'energia potenziale delle sue molecole, è:
∆U = (3/2)nR ΔT
Infine, uniamo le espressioni che abbiamo ottenuto in una:
Q = ∆U + W = (3/2)nR ΔT + nR∆T = (5/2) nR ΔT
In alternativa Q può essere riscritto in termini di massa m, differenza di temperatura e una nuova costante chiamata calore specifico del gas a pressione costante, abbreviato cp, le cui unità sono J / mol K:
Q = m cp ∆T
Non tutti i processi isobarici vengono eseguiti in contenitori chiusi. Infatti, innumerevoli processi termodinamici di ogni tipo avvengono a pressione atmosferica, quindi i processi isobarici sono molto frequenti in natura. Ciò include cambiamenti fisici e chimici alla superficie terrestre, reazioni chimiche nei vasi aperti all'atmosfera e molto altro ancora..
Affinché i processi isobarici si verifichino in sistemi chiusi, i loro confini devono essere sufficientemente flessibili da consentire variazioni di volume senza variare la pressione.
Questo è ciò che è accaduto nell'esperimento del pistone che si muoveva facilmente mentre il gas si espandeva. La stessa cosa accade racchiudendo un gas in una mongolfiera o in una mongolfiera.
Qui abbiamo diversi esempi di processi isobarici:
L'acqua bollente per il tè o le salse da cucina in contenitori aperti sono buoni esempi di processi isobarici, poiché avvengono tutti a pressione atmosferica..
Man mano che l'acqua viene riscaldata, la temperatura e il volume aumentano e se si continua ad aggiungere calore, si raggiunge finalmente il punto di ebollizione, in cui avviene il cambio di fase dell'acqua da liquido a vapore acqueo. Mentre ciò accade, anche la temperatura rimane costante a 100 ° C..
D'altra parte, anche il congelamento dell'acqua è un processo isobarico, sia che avvenga in un lago durante l'inverno che nel frigorifero di casa..
Un altro esempio di processo isobarico è la variazione del volume di un pallone gonfiato con aria quando viene lasciato esposto al Sole. Per prima cosa al mattino, quando non è ancora molto caldo, il pallone ha un certo volume..
Con il passare del tempo e con l'aumentare della temperatura, anche il palloncino si riscalda aumentando il suo volume e tutto questo avviene a pressione costante. Il materiale del palloncino è un buon esempio di un bordo sufficientemente flessibile in modo che l'aria al suo interno, quando riscaldata, si espanda senza modificare la pressione.
L'esperienza può essere svolta anche regolando il palloncino non gonfiato nel beccuccio di una bottiglia di vetro riempita con un terzo d'acqua, che viene riscaldata a bagnomaria. Non appena l'acqua viene riscaldata, il palloncino si gonfia immediatamente, ma bisogna fare attenzione a non riscaldare troppo in modo che non esploda..
È una nave galleggiante senza propulsione, che utilizza correnti d'aria per il trasporto di persone e oggetti. Il pallone è solitamente riempito di aria calda che, essendo più fredda dell'aria circostante, si alza e si espande provocando il sollevamento del pallone..
Sebbene le correnti d'aria dirigano il pallone, ha bruciatori che si attivano per riscaldare il gas quando si desidera salire o mantenere l'altitudine e si disattivano durante la discesa o l'atterraggio. Tutto ciò avviene alla pressione atmosferica, assunta costante ad una certa altezza non distante dalla superficie..
Il vapore viene generato nelle caldaie riscaldando l'acqua e mantenendo la pressione costante. Successivamente, questo vapore svolge un lavoro utilizzabile, ad esempio generando elettricità in impianti termoelettrici o attivando altri meccanismi come locomotive e pompe dell'acqua..
Ci sono 40 litri di gas alla temperatura di 27 ºC. Trovare l'aumento di volume quando si aggiunge calore in modo isobarico fino a raggiungere i 100 ºC.
La legge di Charles viene utilizzata per determinare il volume finale, ma Attenzione: le temperature devono essere espresse in kelvin, aggiungendo semplicemente 273 K a ciascuna:
27 ºC = 27 + 273 K = 300 K
100 ºC = 100 + 273 K = 373 K
A partire dal:
V1/ T1 = VDue/ TDue ⇒ VDue = TDue(V1/ T1) = 373 ºC (40 L / 300 K) = 49,7 L
Infine l'aumento del volume è VDue - V1 = 49,7 L - 40 L = 9,7 L.
Fornito 5,00 x 103 J di energia a un gas ideale per eseguire 2,00 x 103 J lavora sul suo ambiente in un processo isobarico. Si chiede di trovare:
a) La variazione dell'energia interna del gas.
b) La variazione di volume, se ora l'energia interna diminuisce di 4,50 x 103 J e 7,50 x 10 vengono espulsi3 J del sistema, considerando una pressione costante di 1,01 x 105 papà.
Usato ∆U = Q - W e i valori forniti nella dichiarazione sono sostituiti: Q = 5,00 x 103 J e W = 2,00 x 103 J:
=5,00 x 103 J - 2,00 x 103 J = 3,00 x 103 J
Pertanto l'energia interna del gas aumenta di 3,00 x 103 J.
La variazione di volume si riscontra nel lavoro svolto: W = P∆V:
∆U = Q - W = Q - P∆V
L'affermazione afferma che l'energia interna diminuisce, quindi: ∆U= -4,50 x 103 J. Ci dice anche che una certa quantità di calore viene espulsa: Q = -7,50 x 103 J. In entrambi i casi, il segno negativo rappresenta diminuzione e perdita, quindi:
-4,50 x 103 J = -7,50 x 103 J - P∆V
Dove P = 1,01 x 105 Pa. Poiché tutte le unità sono nel Sistema Internazionale, procediamo a risolvere la variazione di volume:
∆V = (-4,50 x 103 J +7,50 x 103 J) / (- 1,01 x 105 papà) = -2,97 x 10-Due m3
Poiché la variazione del volume è negativa, significa che il volume è diminuito, ovvero il sistema si è contratto.
Nessun utente ha ancora commentato questo articolo.