Il probabilità teorica (o Laplace) che si verifica un evento E che appartiene a uno spazio campionario S, in cui tutti gli eventi hanno la stessa probabilità di accadimento, è definito in notazione matematica come: P (E) = n (E) / N (S)
Dove P (E) è la probabilità, data come quoziente tra il numero totale di possibili esiti dell'evento E, che chiamiamo n (E), diviso per il numero totale N (S) di possibili esiti nello spazio campionario S.
La probabilità teorica è un numero reale compreso tra 0 e 1, ma spesso è espressa in percentuale, nel qual caso la probabilità sarà un valore compreso tra 0% e 100%.
Calcolare la probabilità che si verifichi un evento è molto importante in molti campi, come il trading, le compagnie di assicurazione, il gioco d'azzardo e molti altri..
Indice articolo
Un caso illustrativo è il caso di lotterie o lotterie. Supponiamo che 1.000 biglietti vengano emessi per mettere in palio uno smartphone. Poiché l'estrazione viene effettuata in modo casuale, qualsiasi biglietto ha la stessa possibilità di essere un vincitore.
Per trovare la probabilità che una persona che acquista un biglietto con il numero 81 sia un vincitore, il seguente calcolo di probabilità teorica:
P (1) = 1 / 1.000 = 0,001 = 0,1%
Il risultato precedente è interpretato come segue: se l'estrazione fosse ripetuta infinite volte, ogni 1.000 volte il biglietto 81 verrebbe selezionato, in media, una volta.
Se per qualche motivo qualcuno acquista tutti i biglietti è certo che vincerà il premio. La probabilità di vincere il premio se hai tutti i biglietti viene calcolata come segue:
P (1.000) = 1.000 / 1.000 = 1 = 100%.
Cioè, quella probabilità 1 o 100% significa che è assolutamente certo che questo risultato si verificherà..
Se qualcuno possiede 500 biglietti, le possibilità di vincere o perdere sono le stesse. La probabilità teorica di vincere il premio in questo caso è calcolata come segue:
P (500) = 500 / 1.000 = ½ = 0,5 = 50%.
Chi non acquista alcun biglietto non ha possibilità di vincita e la sua probabilità teorica è determinata come segue:
P (0) = 0 / 1.000 = 0 = 0%
Hai una moneta con costoso da un lato e scudo o timbrare sull'altro. Quando la moneta viene lanciata, qual è la probabilità teorica che venga fuori testa??
P (costoso) = n (costoso) / N ( faccia + scudo ) = ½ = 0,5 = 50%
Il risultato è interpretato come segue: se si effettuasse un numero enorme di lanci, in media ogni 2 lanci uno di essi uscirà testa.
In termini percentuali, l'interpretazione del risultato è che eseguire un numero infinitamente elevato di lanci, in media su 100 di essi 50 risulterebbe in testa.
In una scatola ci sono 3 biglie blu, 2 biglie rosse e 1 verde. Qual è la probabilità teorica che quando prendi una biglia dalla scatola sia rossa?
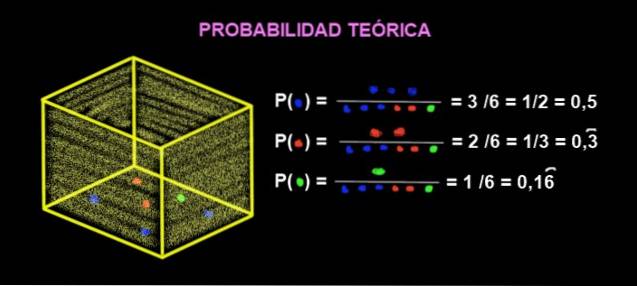
La probabilità che risulti rosso è:
P (rosso) = Numero di casi favorevoli / Numero di casi possibili
Vale a dire:
P (rosso) = Numero di biglie rosse / Numero totale di biglie
Infine, la probabilità che venga disegnata una biglia rossa è:
P (rosso) = 2/6 = ⅓ = 0,3333 = 33,33%
Mentre la probabilità che quando si disegna una biglia verde è:
P (verde) = ⅙ = 0,1666 = 16,66%
Infine, la probabilità teorica di ottenere una biglia blu in un'estrazione alla cieca è:
P (blu) = 3/6 = ½ = 0,5 = 50%
Cioè, per ogni 2 tentativi il risultato sarà blu in uno di essi e un altro colore in un altro tentativo, con la premessa che la biglia estratta viene sostituita e che il numero di prove è molto, molto grande..
Determina la probabilità che quando si tira un dado si ottenga un valore inferiore o uguale a 4.
Per calcolare la probabilità che questo evento si verifichi, verrà applicata la definizione di probabilità teorica:
P (≤4) = Numero di casi favorevoli / Numero di casi possibili
P (≤5) = 5/6 = = 83,33%
Trova la probabilità che su due lanci consecutivi di un normale dado a sei facce, 5 tiri 2 volte.
Per rispondere a questo esercizio, è conveniente creare una tabella che mostri tutte le possibilità. La prima cifra indica il risultato del primo dado e la seconda il risultato dell'altro.
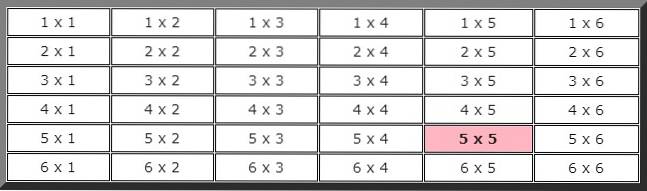
Per calcolare la probabilità teorica occorre conoscere il numero totale di casi possibili, in questo caso, come si può vedere dalla tabella precedente, ci sono 36 possibilità.
Anche osservando la tabella si può dedurre che il numero di casi favorevoli all'evento che nei due lanci consecutivi ne esce 5 è solo 1, evidenziato con colore, quindi la probabilità che questo evento si verifichi è:
P (5 x 5) = 1/36.
Questo risultato potrebbe anche essere stato raggiunto utilizzando una delle proprietà della probabilità teorica, che afferma che la probabilità combinata di due eventi indipendenti è il prodotto delle loro probabilità individuali..
In questo caso, la probabilità che il primo lancio tiri 5 è ⅙. Il secondo lancio è completamente indipendente dal primo, quindi anche la probabilità che il 5 venga lanciato nel secondo è ⅙. Quindi la probabilità combinata è:
P (5 × 5) = P (5) P (5) = (1/6) (1/6) = 1/36.
Trova la probabilità che al primo lancio venga lanciato un numero inferiore a 2 e al secondo un numero maggiore di 2.
Anche in questo caso si deve costruire una tabella degli eventi possibili, dove vengono evidenziati quelli in cui il primo tiro era minore di 2 e nel secondo maggiore di 2..
In totale ci sono 4 possibilità su un totale di 36. Cioè, la probabilità di questo evento è:
P (<2 ; >2) = 4/36 = 1/9 = 0,1111 = 11,11%
Usando il teorema di probabilità che afferma:
La probabilità di accadimento di due eventi indipendenti è uguale al prodotto delle singole probabilità.
Lo stesso risultato si ottiene:
P (<2) P(>2) = (1/6) (4/6) = 4/36 = 0,1111 = 11,11%
Il valore ottenuto con questa procedura coincide con il risultato precedente, attraverso la definizione teorica o classica di probabilità.
Qual è la probabilità che quando si lanciano due dadi la somma dei valori sia 7.
Per trovare la soluzione in questo caso è stata stilata una tabella delle possibilità in cui sono stati indicati a colori i casi che soddisfano la condizione che la somma dei valori sia 7.
Guardando la tabella, si possono contare 6 casi possibili, quindi la probabilità è:
P (I + II: 7) = 6/36 = 1/6 = 0,1666 = 16,66%
Nessun utente ha ancora commentato questo articolo.