
Perimetro del cerchio come estrarlo e formule, esercizi risolti

Il perimetro del cerchio è l'insieme di punti che formano il contorno di un cerchio ed è anche noto come lunghezza della circonferenza. Dipende dal raggio, poiché una circonferenza maggiore avrà ovviamente un contorno più ampio.
Essere P il perimetro di un cerchio e R il raggio di esso, quindi possiamo calcolare P con la seguente equazione:
P = 2π.R

Dove π è un numero reale (leggi “pi”) che vale circa 3,1416… I puntini di sospensione sono dovuti al fatto che π ha infinite cifre decimali. Pertanto, quando si eseguono calcoli, è necessario arrotondare il suo valore.
Tuttavia, per la maggior parte delle applicazioni, è sufficiente prendere l'importo qui indicato, oppure utilizzare tutti i decimali che restituisce la calcolatrice con cui si sta lavorando..
Se invece di avere il raggio si preferisce utilizzare il diametro D, che sappiamo essere il doppio del raggio, il perimetro si esprime come segue:
P = π.2 R = π.D
Poiché il perimetro è una lunghezza, deve sempre essere espresso in unità come metri, centimetri, piedi, pollici e altro, a seconda del sistema preferito..
Indice articolo
- 1 Circonferenze e cerchi
- 2 Esercizi dimostrativi per il calcolo del perimetro del cerchio
- 2.1 - Esercizio 1
- 2.2 - Esercizio 2
- 2.3 - Esercizio 3
- 3 Applicazioni
- 4 Riferimenti
Circonferenze e cerchi
Questi sono spesso termini usati in modo intercambiabile, cioè come sinonimi. Ma succede che ci sono differenze tra loro.
La parola "perimetro" deriva dal greco "peri" che significa contorno e "metro" o misura. La circonferenza è il contorno o il perimetro del cerchio. Formalmente è definito come segue:
Un cerchio è l'insieme di punti con la stessa distanza da un punto chiamato centro, essendo questa distanza il raggio della circonferenza.
Da parte sua, il cerchio è definito come segue:
Un cerchio è l'insieme di punti la cui distanza da un punto chiamato centro è minore o uguale a una distanza fissa chiamata radio.
Il lettore può vedere la sottile differenza tra i due concetti. La circonferenza si riferisce solo all'insieme dei punti del bordo, mentre il cerchio è l'insieme dei punti dal bordo verso l'interno, di cui la circonferenza è il confine.
Esercizi ddimostrazione del calcolo del perimetro del cerchio
Attraverso i seguenti esercizi verranno messi in pratica i concetti sopra descritti, così come alcuni altri che verranno spiegati man mano che si presentano. Partiremo dal più semplice e il grado di difficoltà aumenterà progressivamente.
- Esercizio 1
Trova il perimetro e l'area del cerchio con raggio di 5 cm.
Soluzione
L'equazione data all'inizio viene applicata direttamente:
P = 2π.R= 2π,5 cm = 10 π cm = 31,416 cm
Per calcolare l'area PER viene utilizzata la seguente formula:
PER = π.RDue = π. (5 cm)Due= 25π cmDue= 78,534 cmDue
- Esercizio 2
a) Trova il perimetro e l'area della regione vuota nella figura seguente. Il centro del cerchio ombreggiato si trova nel punto rosso, mentre il centro del cerchio bianco è il punto verde.
b) Ripetere la sezione precedente per la regione ombreggiata.
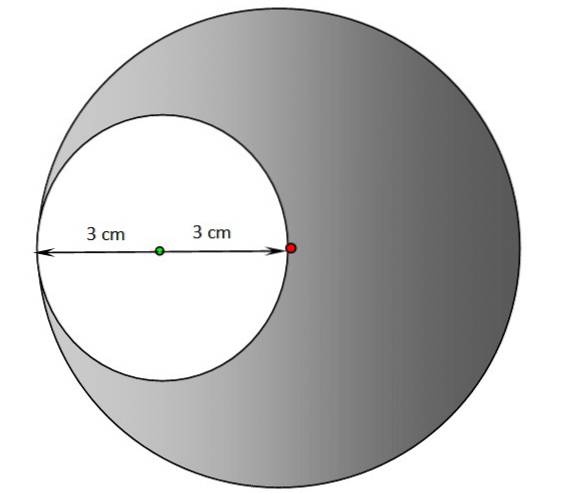
Soluzione
a) Il raggio del cerchio bianco è di 3 cm, quindi applichiamo le stesse equazioni dell'esercizio 1:
P = 2π.R= 2π,3 cm = 6 π cm = 18,85 cm
PER = π.RDue = π. (3 cm)Due= 9π cmDue= 28,27 cmDue
b) Per il cerchio ombreggiato, il raggio è di 6 cm, il suo perimetro è il doppio di quello calcolato nella sezione a):
P = 2π.R= 2π,6 cm = 12 π cm = 37,70 cm
E infine l'area della regione ombreggiata viene calcolata come segue:
- Per prima cosa troviamo l'area del cerchio ombreggiato come se fosse completa, che chiameremo A ', in questo modo:
PER' = π.RDue= π. (6 cm)Due = 36π cmDue= 113,10 cmDue
- Poi alla zona PER' Viene sottratta l'area del cerchio bianco, precedentemente calcolata nella sezione a), in questo modo si ottiene l'area richiesta, che verrà indicata semplicemente con A:
A = LA '- 28,27 cmDue = 113,10-28,27 cmDue = 84,83 cmDue
- Esercizio 3
Trova l'area e il perimetro della regione ombreggiata nella figura seguente:
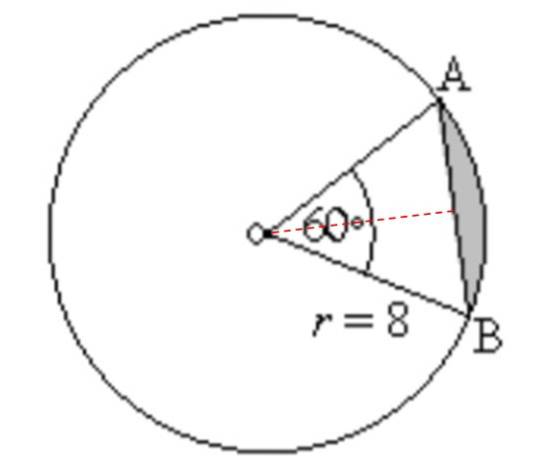
Soluzione
Calcolo dell'area della regione ombreggiata
Per prima cosa calcoliamo l'area di settore circolare o cuneo, tra i segmenti rettilinei OA e OB e il segmento circolare AB, come mostrato nella figura seguente:
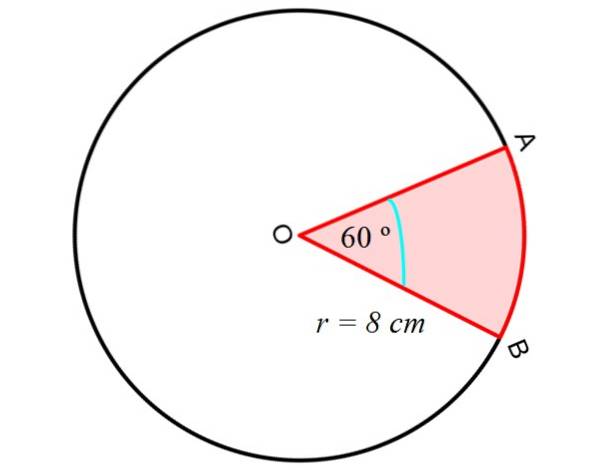
Per questo viene utilizzata la seguente equazione, che ci fornisce l'area di un settore circolare, conoscendo il raggio R e l'angolo centrale tra i segmenti OA e OB, ovvero due dei raggi della circonferenza:
PER settore circolare = Π.RDue. (αº / 360º)
Dove αº è l'angolo centrale -è centrale perché il suo vertice è il centro della circonferenza- tra due raggi.
Passaggio 1: calcola l'area del settore circolare
Pertanto, l'area del settore mostrata in figura è:
PER settore circolare = Π.RDue. (αº / 360º) = π. (8 cm)Due. (60º / 360º) = (64/6) π cmDue= 33,51 cmDue
Passaggio 2: calcola l'area del triangolo
Successivamente calcoleremo l'area del triangolo bianco nella figura 3. Questo triangolo è equilatero e la sua area è:
PER triangolo = (1/2) base x altezza
L'altezza è la linea tratteggiata rossa vista in figura 4. Per trovarla puoi usare il teorema di Pitagora, ad esempio. Ma non è l'unico modo.
Il lettore attento avrà notato che il triangolo equilatero è diviso in due triangoli rettangoli identici, la cui base è di 4 cm:
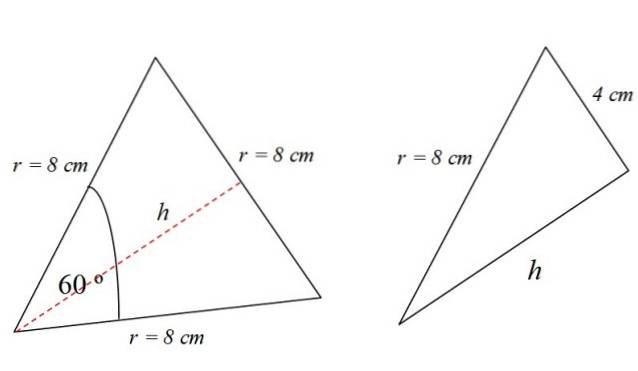
In un triangolo rettangolo, il teorema di Pitagora è soddisfatto, quindi:

PER triangolo = (1/2) base x altezza = (1/2) 8 cm x 6,93 cm = 27,71 cmDue.
Passaggio 3: calcolo dell'area ombreggiata
Basta sottrarre l'area maggiore (quella del settore circolare) dall'area minore (quella del triangolo equilatero): A regione ombreggiata = 33,51 cmDue - 27,71 cmDue = 5,80 cmDue.
Calcolo del perimetro della regione ombreggiata
Il perimetro ricercato è la somma del lato rettilineo di 8 cm e dell'arco di circonferenza AB. Ora, la circonferenza completa sottende 360º, quindi un arco che sottende 60º è un sesto della lunghezza totale, che sappiamo essere 2.π.R:
AB = 2.π.R / 6 = 2.π.8 cm / 6 = 8,38 cm
In sostituzione, il perimetro della regione ombreggiata è:
P = 8 cm + 8,38 cm = 16,38 cm.
Applicazioni
Il perimetro, come l'area, è un concetto molto importante nella geometria e con molte applicazioni nella vita quotidiana..
Artisti, designer, architetti, ingegneri e tante altre persone fanno uso del perimetro durante lo sviluppo del loro lavoro, soprattutto quello di un cerchio, poiché la forma rotonda è ovunque: dalla pubblicità, al cibo ai macchinari.

Per conoscere direttamente la lunghezza di una circonferenza, è sufficiente avvolgerla con un filo o uno spago, quindi estendere questo filo e misurarlo con un metro a nastro. L'altra alternativa è misurare il raggio o il diametro del cerchio e utilizzare una delle formule sopra descritte..
Nel lavoro quotidiano, il concetto di perimetro viene utilizzato quando:
-Lo stampo giusto viene scelto per una certa dimensione di pizza o torta.
-Verrà progettata una strada urbana, calcolando le dimensioni di una fiala dove le auto possono girare per cambiare direzione.
-Sappiamo che la Terra gira intorno al Sole in un'orbita approssimativamente circolare - le orbite planetarie sono in realtà ellittiche, secondo le leggi di Keplero - ma la circonferenza è un'ottima approssimazione per la maggior parte dei pianeti..
-La misura appropriata di un anello viene scelta per essere acquistata in un negozio online.
-Scegliamo una chiave della giusta dimensione per allentare un dado.
E tanti altri.
Riferimenti
- Tutorial di matematica gratuiti. Area e perimetro di un cerchio - Calcolatore della geometria. Recupero da: Analymath.com.
- Math Open Reference. Circonferenza, perimetro di un cerchio. Estratto da: mathopenref.com.
- Monterey Institute. Perimetro e area. Estratto da: montereyinstitute.org.
- Scienza. Come trovare il perimetro di un cerchio. Estratto da: sciencing.com.
- Wikipedia. Circonferenza. Estratto da: en.wikipedia.org.



Nessun utente ha ancora commentato questo articolo.