
Papomudas Come risolverli ed esercizi
Il papomudas è una procedura per risolvere espressioni algebriche. Le sue sigle indicano l'ordine di priorità delle operazioni: parentesi, potenze, moltiplicazione, divisione, addizione e sottrazione. Usando questa parola puoi facilmente ricordare l'ordine in cui devi risolvere un'espressione composta da più operazioni.
Generalmente, nelle espressioni numeriche, si possono trovare più operazioni aritmetiche insieme, come addizione, sottrazione, moltiplicazione e divisione, che possono anche essere frazioni, potenze e radici. Per risolverli è necessario seguire una procedura che garantisca la correttezza dei risultati..

Un'espressione aritmetica composta da una combinazione di queste operazioni deve essere risolta secondo l'ordine di priorità, noto anche come gerarchia delle operazioni, stabilito molto tempo fa nelle convenzioni universali. Pertanto, tutte le persone possono seguire la stessa procedura e ottenere lo stesso risultato.
Indice articolo
- 1 Caratteristiche
- 2 Come risolverli?
- 3 Applicazione
- 3.1 Espressioni contenenti addizioni e sottrazioni
- 3.2 Espressioni contenenti addizioni, sottrazioni e moltiplicazioni
- 3.3 Espressioni contenenti addizioni, sottrazioni, moltiplicazioni e divisioni
- 3.4 Espressioni contenenti addizioni, sottrazioni, moltiplicazioni, divisioni e potenze
- 3.5 Espressioni che utilizzano simboli di raggruppamento
- 4 esercizi
- 4.1 Primo esercizio
- 4.2 Secondo esercizio
- 4.3 Terzo esercizio
- 5 Riferimenti
Caratteristiche
Papomudas è una procedura standard che stabilisce l'ordine da seguire quando si risolve un'espressione, che è composta da una combinazione di operazioni come addizione, sottrazione, moltiplicazione e divisione..
Con questa procedura si stabilisce l'ordine di priorità di un'operazione rispetto alle altre nel momento in cui esse saranno esito; cioè, ogni operazione ha un turno o un livello gerarchico da risolvere.
L'ordine in cui devono essere risolte le diverse operazioni di un'espressione è dato da ogni acronimo della parola papomudas. Quindi, devi:
1- Pa: parentesi, parentesi o parentesi graffe.
2- Po: poteri e radici.
3- Mu: moltiplicazioni.
4- D: divisioni.
5- A: aggiunte o aggiunte.
6- S: sottrazioni o sottrazioni.
Questa procedura è anche chiamata in inglese PEMDAS; per ricordare facilmente questa parola è associata alla frase: "Pleggere Excuse MY Dorecchio PERunt Salleato”, Dove ogni lettera iniziale corrisponde a un'operazione aritmetica, allo stesso modo delle papomuda.
Come risolverli?
Sulla base della gerarchia stabilita dai papomuda per risolvere le operazioni di un'espressione, è necessario soddisfare il seguente ordine:
- Tutte le operazioni all'interno dei simboli di raggruppamento, come parentesi, parentesi graffe, parentesi quadre e barre frazionarie, devono essere prima risolte. Quando ci sono simboli di raggruppamento all'interno di altri, è necessario iniziare a calcolare dall'interno verso l'esterno.
Questi simboli servono per cambiare l'ordine in cui vengono risolte le operazioni, perché quello che c'è al loro interno deve essere sempre risolto per primo..
- Quindi i poteri e le radici sono risolti.
- In terzo luogo si risolvono le moltiplicazioni e le divisioni. Questi hanno lo stesso ordine di priorità; quindi, quando queste due operazioni si trovano in un'espressione, quella che appare per prima deve essere risolta, leggendo l'espressione da sinistra a destra.
- In ultimo si risolvono le addizioni e le sottrazioni, che hanno anche lo stesso ordine di priorità e, quindi, viene risolta quella che compare per prima nell'espressione, letta da sinistra verso destra.
- Le operazioni non dovrebbero mai essere mescolate quando lette da sinistra a destra, l'ordine di priorità o gerarchia stabilito dai papomuda dovrebbe sempre essere seguito..
È importante ricordare che il risultato di ogni operazione deve essere posto nello stesso ordine rispetto alle altre, e tutti i passaggi intermedi devono essere separati da un segno fino al raggiungimento del risultato finale..
App
La procedura papomudas viene utilizzata quando si dispone di una combinazione di diverse operazioni. Tenendo conto di come vengono risolti, questo può essere applicato in:
Espressioni contenenti addizioni e sottrazioni
È una delle operazioni più semplici, perché entrambe hanno lo stesso ordine di priorità, in modo tale da dover essere risolta partendo da sinistra verso destra nell'espressione; per esempio:
22-15 + 8 +6 = 21.
Espressioni contenenti addizione, sottrazione e moltiplicazione
In questo caso, l'operazione con la priorità più alta è la moltiplicazione, quindi l'addizione e la sottrazione vengono risolte (a seconda di quale sia la prima nell'espressione). Per esempio:
6 * 4-10 + 8 * 6 - 16 + 10 * 6
= 24-10 + 48-16 + 60
= 106.
Espressioni contenenti addizione, sottrazione, moltiplicazione e divisione
In questo caso hai una combinazione di tutte le operazioni. Inizi risolvendo la moltiplicazione e la divisione che hanno priorità più alta, quindi l'addizione e la sottrazione. Leggendo l'espressione da sinistra a destra, viene risolta in base alla sua gerarchia e posizione all'interno dell'espressione; per esempio:
7 + 10 * 13 - 8 + 40 ÷ 2
= 7 + 130 - 8 + 20
= 149.
Espressioni contenenti addizioni, sottrazioni, moltiplicazioni, divisioni e potenze
In questo caso, uno dei numeri viene elevato a una potenza, che all'interno del livello di priorità deve essere risolta prima, per poi risolvere le moltiplicazioni e le divisioni, e infine le addizioni e le sottrazioni:
4 + 4Due * 12-5 + 90 ÷ 3
= 4 + 16 * 12-5 + 90 ÷ 3
= 4 + 192 - 5 + 30
= 221.
Come i poteri, anche le radici hanno il secondo ordine di priorità; Pertanto, nelle espressioni che li contengono, la moltiplicazione, la divisione, l'addizione e la sottrazione devono essere risolte prima:
5 * 8 + 20 ÷ √16
= 5 * 8 + 20 ÷ 4
= 40 + 5
= 45.
Espressioni che utilizzano simboli di raggruppamento
Quando si utilizzano segni come parentesi, parentesi graffe, parentesi e barre di frazione, ciò che è all'interno di questi viene risolto per primo, indipendentemente dall'ordine di priorità delle operazioni che contiene rispetto a quelle esterne, come se fosse un'espressione separata :
14 ÷ 2 - (8 - 5)
= 14 ÷ 2-3
= 7-3
= 4.
Se ci sono più operazioni al suo interno, devono essere risolte in ordine gerarchico. Quindi vengono risolte le altre operazioni che compongono l'espressione; per esempio:
2 + 9 * (5 + 23 - 24 ÷ 6) - 1
= 2 + 9 * (5 + 8 - 4) - 1
= 2 + 9 * 9 - 1
= 2 + 81 - 1
= 82.
Alcune espressioni utilizzano simboli di raggruppamento all'interno di altri, ad esempio quando è necessario modificare il segno di un'operazione. In questi casi, devi iniziare risolvendo dall'interno verso l'esterno; ovvero semplificando i simboli di raggruppamento che si trovano al centro di un'espressione.
Generalmente, l'ordine per risolvere le operazioni contenute in questi simboli è: prima risolvi ciò che è racchiuso tra parentesi (), poi le parentesi [] e infine le parentesi graffe .
90 - 3*[12 + (5*4) - (4*Due)]
= 90 - 3* [12 + 20 - 8]
= 90 - 3 * 24
= 90-72
= 18.
Formazione
Primo esercizio
Trova il valore della seguente espressione:
ventiDue + √225 - 155 + 130.
Soluzione
Applicando i papomuda, i poteri e le radici devono essere risolti prima, quindi l'addizione e la sottrazione. In questo caso le prime due operazioni appartengono allo stesso ordine, quindi si risolve quella per prima, partendo da sinistra verso destra:
ventiDue + √225 - 155 + 130
= 400 + 15-155 + 130.
Quindi aggiungi e sottrai, partendo anche da sinistra:
400 + 15-155 + 130
= 390.
Secondo esercizio
Trova il valore della seguente espressione:
[- (63 - 36) ÷ (8 * 6 ÷ 16)].
Soluzione
Inizia risolvendo le operazioni che stanno all'interno delle parentesi, seguendo l'ordine gerarchico che hanno secondo i papomuda.
Prima vengono risolte le potenze delle prime parentesi, quindi vengono risolte le operazioni delle seconde parentesi. Poiché appartengono allo stesso ordine, la prima operazione dell'espressione è risolta:
[- (63 - 36) ÷ (8 * 6 ÷ 16)]
= [- (216 - 729) ÷ (8 * 6 ÷ 16)]
= [- (216 - 729) ÷ (48 ÷ 16)]
= [- (-513) ÷ (3)].
Poiché le operazioni tra parentesi sono già state risolte, ora proseguiamo con la divisione che ha una gerarchia più alta rispetto alla sottrazione:
[- (-513) ÷ (3)] = [- (-171)].
Infine, la parentesi che separa il segno meno (-) dal risultato, che in questo caso è negativo, indica che questi segni devono essere moltiplicati. Pertanto, il risultato dell'espressione è:
[- (-171)] = 171.
Terzo esercizio
Trova il valore della seguente espressione:

Soluzione
Inizi risolvendo le frazioni che sono all'interno delle parentesi:
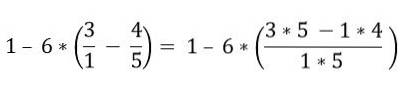
All'interno delle parentesi sono presenti diverse operazioni. Si risolvono prima le moltiplicazioni e poi le sottrazioni; In questo caso la barra della frazione è considerata come un simbolo di raggruppamento e non come una divisione, per questo motivo le operazioni della parte superiore e inferiore devono essere risolte:
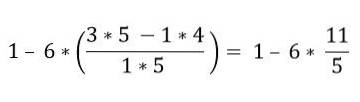
In ordine gerarchico, la moltiplicazione deve essere risolta:
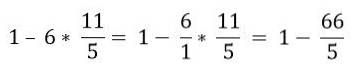
Infine, la sottrazione è risolta:
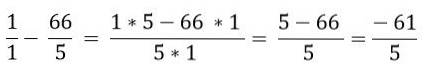
Riferimenti
- Aguirre, H. M. (2012). Matematica finanziaria. Cengage Learning.
- Aponte, G. (1998). Fondamenti di matematica di base. Pearson Education.
- Cabanne, N. (2007). Didattica della matematica.
- Carolina Espinosa, C. C. (2012). Risorse nelle operazioni di apprendimento.
- Huffstetler, K. (2016). La storia dell'ordine delle operazioni: Pemdas. Crea spazio indipendente .
- Madore, B. (2009). GRE Math Workbook. Serie educativa di Barron,.
- Molina, F. A. (s.f.). Progetto Azarquiel, Matematica: primo ciclo. Gruppo Azarquiel.



Nessun utente ha ancora commentato questo articolo.