
Espressione matematica ed esempi di onde unidimensionali
Il onde unidimensionali Sono quelli che si propagano in un'unica direzione indipendentemente dal fatto che la vibrazione avvenga o meno nella stessa direzione di propagazione. Un buon esempio di loro è l'onda che viaggia attraverso una corda tesa come quella di una chitarra..
In un'onda piatta attraversare, le particelle vibrano in direzione verticale (vanno su e giù, vedi la freccia rossa in figura 1), ma è unidimensionale perché il disturbo viaggia in una sola direzione, seguendo la freccia gialla.

Le onde unidimensionali compaiono abbastanza frequentemente nella vita di tutti i giorni. La sezione seguente descrive alcuni esempi di loro e anche di onde che non sono unidimensionali, per stabilire chiaramente le differenze.
Indice articolo
- 1 Esempi di onde unidimensionali e onde non unidimensionali
- 1.1 Onde unidimensionali
- 1.2 Onde non unidimensionali
- 2 Espressione matematica di un'onda unidimensionale
- 2.1 Equazione delle onde unidimensionale
- 2.2 Esempio lavorato
- 3 Riferimenti
Esempi di onde unidimensionali e onde non unidimensionali
Onde unidimensionali
Ecco alcuni esempi di onde unidimensionali che possono essere facilmente osservate:
- Un impulso sonoro che viaggia attraverso una barra diritta, poiché è un disturbo che si propaga per l'intera lunghezza della barra.
- Un'onda che viaggia attraverso un canale d'acqua, anche se lo spostamento della superficie dell'acqua non è parallelo al canale.
- Le onde che si propagano su una superficie o attraverso lo spazio tridimensionale possono anche essere unidimensionali, purché i loro fronti d'onda siano piani paralleli tra loro e viaggiano in una sola direzione..
Onde non unidimensionali
Un esempio di onda non unidimensionale si trova nelle onde che si formano su una superficie di acqua calma quando una pietra viene lasciata cadere. È un'onda bidimensionale con un fronte d'onda cilindrico.

Un altro esempio di onda non unidimensionale è l'onda sonora generata da un petardo esplodendo a una certa altezza. Questa è un'onda tridimensionale con fronti d'onda sferici.
Espressione matematica di un'onda unidimensionale
Il modo più generale per esprimere un'onda unidimensionale che si propaga senza attenuazione nella direzione positiva dell'asse X e con velocità v è, matematicamente:
y (x, t) = f (x - v.t)
In questa espressione Y rappresenta il disturbo nella posizione X Immediatamente t. La forma dell'onda è data dalla funzione F. Ad esempio, la funzione d'onda mostrata nella figura 1 è: y (x, t) = cos (x - v t) e l'immagine dell'onda corrisponde all'istante t = 0.
Viene chiamata un'onda come questa, descritta da una funzione coseno o seno onda armonica. Sebbene non sia l'unica forma d'onda esistente, è della massima importanza, perché qualsiasi altra onda può essere rappresentata come una sovrapposizione o somma di onde armoniche. Si tratta del noto Teorema di Fourier, così usato per descrivere segnali di ogni tipo.
Quando l'onda viaggia nella direzione negativa dell'asse x, cambia semplicemente v per -v in discussione, lasciando:
y (x, t) = g (x + v t)
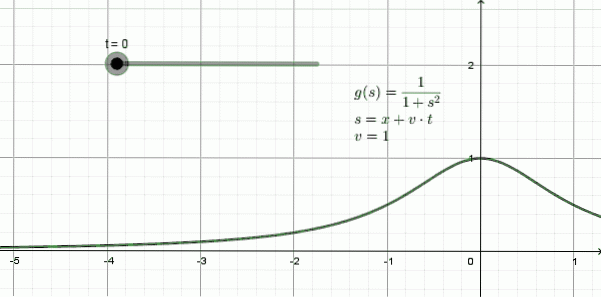
La figura 3 mostra l'animazione di un'onda che viaggia verso sinistra: è una forma chiamata funzione lorentziana e lei l'espressione matematica è:
y (x, t) = 1 / (1 + (x + 1⋅t)Due
In questo esempio la velocità di propagazione è v = 1, -un'unità di spazio per ogni unità di tempo-.
Equazione delle onde unidimensionale
L'equazione delle onde è un'equazione di derivata parziale, la cui soluzione è ovviamente un'onda. Stabilisce la relazione matematica tra la parte spaziale e la parte temporale di essa, e ha la forma:

Esempio funzionante
La seguente è l'espressione generale y (x, t) per un'onda armonica:
y (x, t) = A⋅cos (k⋅x ± ω⋅t + θo)
a) Descrivere il significato fisico dei parametri A, k, ω Y θo.
b) Che significato hanno i segni ± nell'argomento del coseno?
c) Verificare che l'espressione data sia effettivamente la soluzione dell'equazione delle onde della sezione precedente e trovare la velocità v propagazione.
Soluzione a)
Le caratteristiche dell'onda si trovano nei seguenti parametri:
-PER rappresenta il ampiezza o "altezza d'onda".
-cosa c'è dentro numero d'onda ed è correlato alla lunghezza d'onda λ attraverso k = 2π / λ.
-ω è la ffrequenza angolare ed è correlato al periodo T oscillazione dell'onda di
ω = 2π / T.
-θo è il fase iniziale, che è correlato al punto di partenza dell'onda.
Soluzione b)
Viene preso un segno negativo se l'onda viaggia nella direzione positiva dell'asse X e un segno positivo in caso contrario..
Soluzione c)
Verificare che l'espressione data sia una soluzione dell'equazione delle onde è semplice: viene presa la derivata parziale della funzione y (x, t) rispetto a x due volte, parzialmente ri-derivato rispetto a t due volte, quindi combinare entrambi i risultati per ottenere un'uguaglianza:
Seconda derivata rispetto a x: ∂Duey / ∂xDue= -KDue. PER⋅cos (k⋅x ± ω⋅t + θo)
Derivata seconda rispetto at: ∂Duey / ∂tDue= -ΩDue. PER⋅cos (k⋅x ± ω⋅t + θo)
Questi risultati vengono sostituiti nell'equazione delle onde:
-KDue. PER⋅cos (k⋅x ± ω⋅t + θo) = (1 / vDue) (-ωDue. PER⋅cos (k⋅x ± ω⋅t + θo))
Tanto PER poiché il coseno è semplificato, poiché compaiono su entrambi i lati dell'uguaglianza e l'argomento del coseno è lo stesso, quindi l'espressione si riduce a:
-KDue = (1 / vDue) (-ωDue)
Ciò consente di ottenere un'equazione per v in termini di ω Y K:
vDue = ωDue / KDue
v = ± ω / k
Riferimenti
- E-educativo. Equazione delle onde armoniche unidimensionali. Estratto da: e-ducativa.catedu.es
- L'angolo della fisica. Corsi di onde. Estratto da: fisicaparatontos.blogspot.com.
- Figueroa, D. 2006. Waves and Quantum Physics. Serie: Fisica per la scienza e l'ingegneria. A cura di Douglas Figueroa. Simon Bolivar University. Caracas Venezuela.
- Physics Lab. Moto ondoso. Estratto da: fisicalab.com.
- Peirce, A. Lezione 21: L'equazione dell'onda unidimensionale: la soluzione di D'Alembert. Recupero da: ubc.ca.
- Equazione delle onde. Estratto da: en.wikipedia.com



Nessun utente ha ancora commentato questo articolo.