
Formule, caratteristiche, tipi, esempi di onde stazionarie
Il onde stazionarie Sono onde che si propagano in un mezzo limitato, andando e venendo in una parte dello spazio, a differenza delle onde viaggianti, che nel propagarsi si allontanano dalla sorgente che le ha originate e non vi ritornano.
Sono la base dei suoni prodotti negli strumenti musicali, poiché sorgono facilmente nelle corde fisse, ad un'estremità o ad entrambe. Sono anche creati in membrane a tenuta come fusti o all'interno di tubi e strutture come ponti ed edifici..
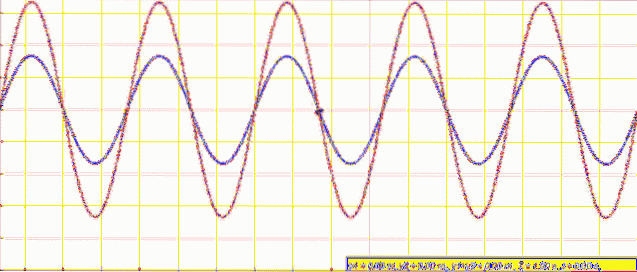
Quando hai una corda fissa ad entrambe le estremità, come quella di una chitarra, ad esempio, si creano onde con ampiezza e frequenza identiche, che viaggiano in direzioni opposte e si combinano per produrre un fenomeno chiamato interferenza.
Se le onde sono in fase, i picchi e le valli sono allineati e danno come risultato un'onda con ampiezza doppia. In tal caso si parla di interferenza costruttiva.
Ma se le onde interferenti sono fuori fase, i picchi di una incontrano le valli delle altre e l'ampiezza risultante è zero. Si tratta quindi di interferenze distruttive.
Indice articolo
- 1 Formule ed equazioni
- 1.1 Espressione matematica dell'onda stazionaria
- 2 Posizione dei nodi e delle pance
- 2.1 Modalità normali su una stringa
- 2.2 Velocità e frequenza
- 3 Caratteristiche delle onde stazionarie
- 4 tipi
- 4.1 Onde stazionarie in una dimensione
- 4.2 Onde stazionarie in due e tre dimensioni
- 5 Esempi di onde stazionarie
- 5.1 Funi fisse
- 5.2 Strumenti musicali
- 5.3 Edifici e ponti
- 5.4 Seiches
- 5.5 Fishbowls
- 6 Esercizio risolto
- 6.1 Soluzione a
- 6.2 Soluzione b
- 6.3 Soluzione c
- 7 Riferimenti
Formule ed equazioni
Gli elementi principali dell'onda per rappresentarla nello spazio e nel tempo sono la sua ampiezza A, la sua lunghezza d'onda λ e la sua frequenza angolare ω.
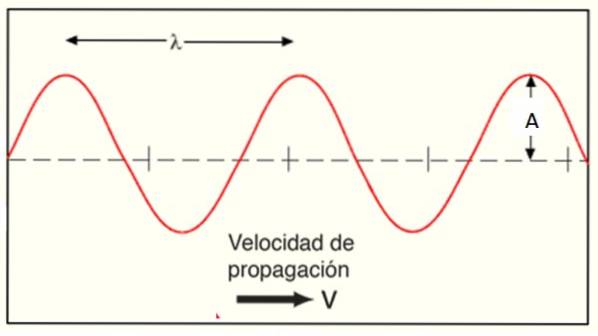
Nella rappresentazione matematica si preferisce usare k, rispetto a numero d'onda o il numero di volte in cui si verifica l'onda per unità di lunghezza. Ecco perché è definito attraverso la lunghezza d'onda λ che è la distanza tra due valli o due creste:
k = 2π / λ
Mentre il frequenza angolare si riferisce al periodo o alla durata di un'oscillazione completa, come ad esempio:
ω = 2π / T
E anche la frequenza f è data da:
f = ω / 2π
Perciò:
f = 1 / T
Anche le onde si muovono con velocità v secondo:
v = λ.f
Espressione matematica dell'onda stazionaria
Matematicamente possiamo esprimere un'onda usando la funzione seno o la funzione coseno. Supponiamo di avere onde di uguale ampiezza A, lunghezza d'onda λ e frequenza ω, che si propagano lungo una stringa e in direzioni opposte:
Y1 = A sin (kx - ωt)
YDue = A sin (kx + ωt)
Quando li aggiungiamo troviamo l'onda risultante eR:
YR = e1 + YDue = A sin (kx - ωt) + A sin (kx + ωt)
C'è un'identità trigonometrica per trovare la somma:
sin α + sin β = 2 sin (α + β) / 2. cos (α - β) / 2
Con questa identità, l'onda risultante yR resti:
YR = [2A sin kx]. cos ωt
Posizione dei nodi e delle pance
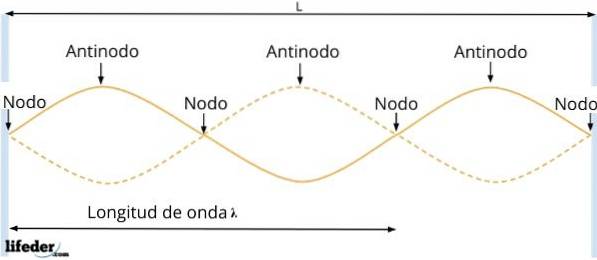
L'onda risultante ha ampiezza AR = 2 Asen kx, che dipende dalla posizione della particella. Quindi, nei punti per cui sin kx = 0, l'ampiezza dell'onda svanisce, cioè non c'è vibrazione.
Questi punti sono:
kx = π, 2π, 3π…
Poiché k = 2 π / λ:
(2 π / λ) x = π, 2π, 3π…
x = λ / 2, λ, 3λ / 2 ...
L'interferenza distruttiva si verifica in tali punti e viene chiamata nodi. Sono separati da una distanza pari a λ / 2, come dedotto dal risultato precedente.
E tra due nodi consecutivi ci sono gli antinodi o pance, in cui l'ampiezza dell'onda è massima, poiché lì si verifica un'interferenza costruttiva. Si verificano quando:
sin kx = ± 1
kx = ± π / 2, 3π / 2, 5π / 2…
Anche in questo caso k = 2 π / λ e quindi:
x = λ / 4, 3λ / 4, 5λ / 4, ...
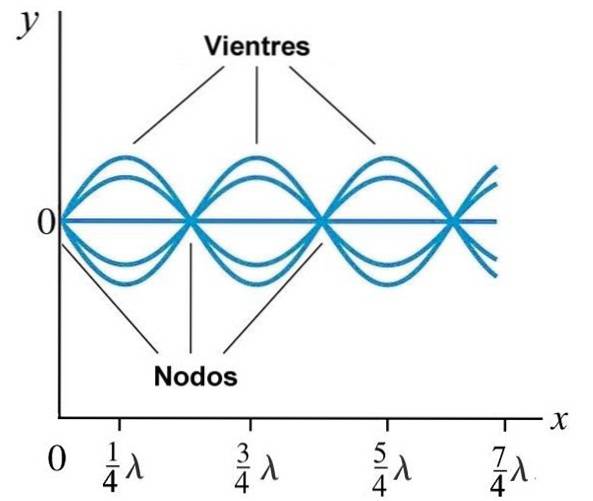
Modalità normali su una stringa
Le condizioni al contorno nella stringa determinano come sono le lunghezze d'onda e le frequenze. Se una corda di lunghezza L è fissata ad entrambe le estremità, non può vibrare con alcuna frequenza, perché i punti in cui è fissata la corda sono già nodi.
Inoltre la separazione tra nodi adiacenti è λ / 2, e tra nodo e pancia è λ / 4, in questo modo solo per determinate lunghezze d'onda si producono onde stazionarie: quelle in cui un intero n di λ / 2 rientra tra:
(λ / 2) = L, con n = 1, 2, 3, 4 ... .
Perciò:
λ = 2L / n
Armoniche
Vengono chiamati i diversi valori che λ assume armoniche. Quindi abbiamo:
-Prima armonica: λ = 2L
-Seconda armonica: λ = L
-Terza armonica: λ = 2 L / 3
-Quarta armonica: λ = L / 2
E così via.
Velocità e frequenza
Anche se l'onda stazionaria non sembra muoversi, l'equazione è ancora valida:
v = λ. F
Perciò:
v = (2L / n). F
f = nv / 2L
Ora, si può dimostrare che la velocità con cui un'onda viaggia in una corda dipende dalla tensione T in essa e dalla sua densità lineare di massa μ (massa per unità di lunghezza) come:

Perciò:

Caratteristiche delle onde stazionarie
-Quando le onde sono stazionarie, l'onda risultante non si propaga come i suoi componenti, che vanno da una parte all'altra. Ci sono punti dove y = 0 perché non c'è vibrazione: i nodi, in altre parole, l'ampiezza AR diventa zero.
-L'espressione matematica di un'onda stazionaria è costituita dal prodotto di una parte spaziale (che dipende dalla coordinata x o dalle coordinate spaziali) e da una parte temporale.
-Tra i nodi l'onda nera risultante oscilla in un punto, mentre le onde che vanno da un lato all'altro sono fuori fase lì..
-L'energia non viene trasportata proprio ai nodi, poiché questo è proporzionale al quadrato dell'ampiezza, ma è intrappolata tra i nodi.
-La distanza tra i nodi adiacenti è la metà della lunghezza d'onda.
-Anche i punti in cui è fissato l'accordo sono considerati nodi..
Tipi
Onde stazionarie in una dimensione
Le onde in una stringa fissa sono esempi di onde stazionarie in una dimensione, la cui descrizione matematica è stata offerta nelle sezioni precedenti..
Onde stazionarie in due e tre dimensioni
Le onde stazionarie possono anche essere presentate in due e tre dimensioni, essendo la loro descrizione matematica un po 'più complessa.
Esempi di onde stazionarie
Corde fisse
-Una fune fissata ad un'estremità che viene fatta oscillare manualmente o con un pistone dall'altra genera onde stazionarie lungo la sua lunghezza.
Strumenti musicali

-Anche suonare strumenti a corda come chitarra, arpa, violino e pianoforte crea onde stazionarie, poiché hanno corde regolate a diverse tensioni e fissate ad entrambe le estremità.
Le onde stazionarie vengono create anche nei tubi con aria, come i tubi degli organi..
Edifici e ponti
Le onde stazionarie sorgono in strutture come ponti ed edifici. Un caso degno di nota è stato quello del ponte sospeso di Tacoma Narrows vicino alla città di Seattle, negli Stati Uniti. Poco dopo essere stato inaugurato nel 1940, questo ponte è crollato a causa delle onde stazionarie create all'interno dal vento..
La frequenza del vento era accoppiata con la frequenza naturale del ponte, creando onde stazionarie al suo interno, che aumentavano di ampiezza fino al collasso del ponte. Il fenomeno è noto come risonanza.
Seiches
Nei porti c'è un fenomeno molto curioso chiamato seiche, in cui le onde del mare producono grandi oscillazioni. Ciò è dovuto al fatto che le acque del porto sono abbastanza chiuse, sebbene le acque oceaniche penetrino di volta in volta attraverso l'ingresso del porto..
Le acque del porto si muovono con la propria frequenza, proprio come quelle dell'oceano. Se entrambe le acque eguagliano le loro frequenze, una grande onda stazionaria viene prodotta dalla risonanza, come è successo con il ponte di Tacoma..
Il seiches Possono anche verificarsi in laghi, bacini idrici, piscine e altri specchi d'acqua limitati in superficie..
Acquari
Le onde stazionarie possono essere create in un acquario trasportato da una persona, se la frequenza con cui la persona cammina è uguale alla frequenza dell'oscillazione dell'acqua.
Esercizio risolto
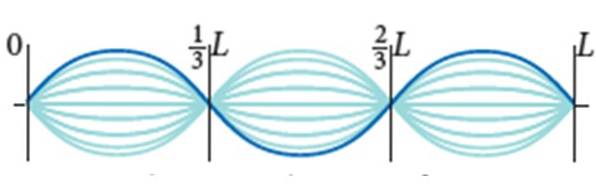
Una corda di chitarra ha L = 0,9 me una densità di massa lineare μ = 0,005 kg / m. È sottoposto a 72 N di tensione e il suo modo di vibrazione è quello mostrato in figura, con ampiezza 2A = 0,5 cm.
Trova:
a) Velocità di propagazione
b) Frequenza d'onda
c) La corrispondente equazione delle onde stazionarie.
Soluzione a
Attraverso:

È ottenuto;
v = [72 N / (0,005 kg / m)]1/2 = 120 m / s.
Soluzione b
La distanza tra due nodi adiacenti è λ / 2, quindi:
(2/3) L - (1/3) L = λ / 2
(1/3) L = λ / 2
λ = 2L / 3 = 2 x 0,90 m / 3 = 0,60 m.
Poiché v = λ.f
f = (120 m / s) / 0,60 m = 200 s-1= 200 Hz.
Soluzione c
L'equazione è:
YR = [2A sin kx]. cos ωt
Dobbiamo sostituire i valori:
k = 2π / λ = k = 2π / 0,60 m = 10 π / 3
f = ω / 2π
ω = 2π x 200 Hz = 400 π Hz.
L'ampiezza 2A è già data dall'affermazione:
2A = 0,5 cm = 5 x 10 -3 m.
Perciò:
YR = 5 x 10 -3 m. sin [(10π / 3) x]. cos (400πt) =
= 0,5 cm. sin [(10π / 3) x]. cos (400πt)
Riferimenti
- Bauer, W. 2011. Fisica per l'ingegneria e le scienze. Volume 1. Mc Graw Hill.
- Figueroa, D. (2005). Serie: Fisica per la scienza e l'ingegneria. Volume 7. Onde e fisica quantistica. A cura di Douglas Figueroa (USB).
- Giancoli, D. 2006. Fisica: principi con applicazioni. 6 °. Ed prentice hall.
- Serway, R., Jewett, J. (2008). Fisica per la scienza e l'ingegneria. Volume 1. 7th. Ed. Cengage Learning.
- Tipler, P. (2006) Physics for Science and Technology. 5a Ed. Volume 1. Editoriale Reverté.
- Wikipedia. Seiche. Estratto da: es.wikipedia.org.


Nessun utente ha ancora commentato questo articolo.