
Proprietà dei numeri immaginari, applicazioni, esempi
Il numeri immaginari sono quelli che danno una soluzione all'equazione in cui l'ignoto, al quadrato, è uguale a un numero reale negativo. L'unità immaginaria è i = √ (-1).
Nell'equazione: zDue= - a, z è un numero immaginario che si esprime come segue:
z = √ (-a) = i√ (a)
Essere per un numero reale positivo. sì a = 1, poi z = i, dove io è l'unità immaginaria.
In generale, un numero immaginario puro z è sempre espresso nella forma:
z = y⋅i
Dove Y è un numero reale e io è l'unità immaginaria.
Proprio come i numeri reali sono rappresentati su una linea, chiamata vero dritto, in modo analogo i numeri immaginari sono rappresentati sul linea immaginaria.
Il linea immaginaria è sempre ortogonale (forma a 90º) al vero dritto e le due linee definiscono un piano cartesiano chiamato piano complesso.
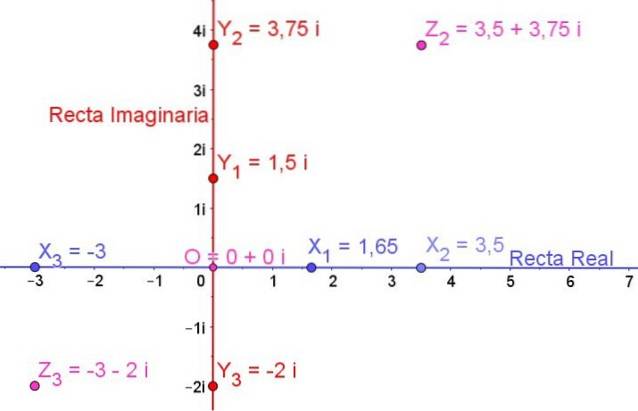
Nella figura 1 è mostrato il piano complesso e su di esso sono rappresentati alcuni numeri reali, alcuni numeri immaginari e anche alcuni numeri complessi:
X1, XDue, X3 sono numeri reali
Y1, YDue, Y3 sono numeri immaginari
ZDue e Z3 sono numeri complessi
Il numero O è lo zero reale ed è anche lo zero immaginario, quindi l'origine O è lo zero complesso espresso da:
0 + 0i
Indice articolo
- 1 Proprietà
- 1.1 Addizione e sottrazione dell'immaginario
- 1.2 Prodotto di immaginari
- 1.3 Prodotto di un numero reale da un altro immaginario
- 1.4 Empowerment di un immaginario
- 1.5 Somma di un numero reale e di un numero immaginario
- 2 Applicazioni
- 3 Esercizi con numeri immaginari
- 3.1 - Esercizio 1
- 3.2 - Esercizio 2
- 3.3 - Esercizio 3
- 3.4 - Esercizio 4
- 3.5 - Esercizio 5
- 3.6 - Esercizio 6
- 4 Riferimenti
Proprietà
L'insieme dei numeri immaginari è indicato da:
I = …, -3i,…, -2i,…., - i,…., 0i,…., I,…., 2i,…., 3i,…
E puoi definire alcune operazioni su questo insieme numerico. Un numero immaginario non si ottiene sempre da queste operazioni, quindi esaminiamole un po 'più in dettaglio:
Addizione e sottrazione dell'immaginario
I numeri immaginari possono essere aggiunti e sottratti l'uno dall'altro, ottenendo un nuovo numero immaginario. Per esempio:
3i + 2i = 5i
4i - 7i = -3i
Prodotto dell'immaginario
Quando si crea il prodotto di un numero immaginario con un altro, il risultato è un numero reale. Facciamo la seguente operazione per verificarlo:
2i x 3i = 6 x iDue = 6 x (√ (-1))Due = 6 x (-1) = -6.
E come possiamo vedere, -6 è un numero reale, sebbene sia stato ottenuto moltiplicando due numeri immaginari puri.
Prodotto di un numero reale da un altro immaginario
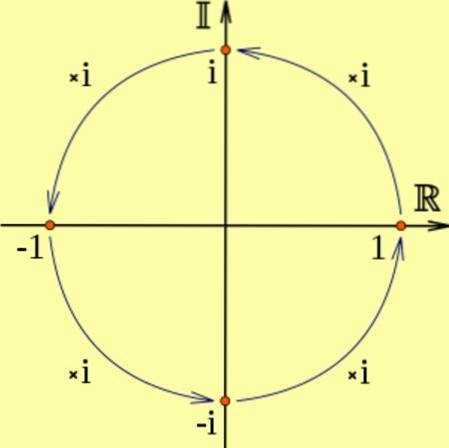
Se un numero reale viene moltiplicato per i, il risultato sarà un numero immaginario, che corrisponde a una rotazione di 90 gradi in senso antiorario.
Ed è che ioDue corrisponde a due rotazioni consecutive di 90 gradi, che equivale a moltiplicare per -1, cioè iDue = -1. Può essere visto nel diagramma seguente:
Per esempio:
-3 x 5i = -15i
-3 x i = -3i.
Empowerment di un immaginario
Puoi definire il potenziamento di un numero immaginario in un esponente intero:
io1 = i
ioDue = io x io = √ (-1) x √ (-1) = -1
io3 = io x iDue = -i
io4 = iDue x iDue = -1 x -1 = 1
io5 = i x i4 = i
In generale devi ion = i ^ (n mod 4), dove mod è il resto della divisione tra n Y 4.
Il potenziamento intero negativo può essere eseguito anche:
io-1 = 1 / i1 = io / (io x io1) = i / (iDue) = i / (-1) = -i
io-Due = 1 / iDue = 1 / (-1) = -1
io-3= 1 / i3 = 1 / (- i) = (-1) / i = -1 x i-1 = (-1) x (-i) = i
In generale, il numero immaginario b⋅i elevato alla potenza n è:
(b⋅i) in = bn ion = bn io ^ (n mod 4)
Alcuni esempi sono i seguenti:
(5 i)12 = 512 io12 = 512 io0 = 512 x 1 = 244140625
(5 i)undici = 5undici ioundici = 5undici io3 = 5undici x (-i) = -48828125 i
(-2 i)10 = -210 io10 = 210 ioDue = 1024 x (-1) = -1024
Somma di un numero reale e di un numero immaginario
Quando aggiungi un numero reale con uno immaginario, il risultato non è né reale né immaginario, è un nuovo tipo di numero chiamato numero complesso.
Ad esempio, se X = 3.5 e Y = 3.75i, il risultato è il numero complesso:
Z = X + Y = 3,5 + 3,75 i
Nota che nella somma le parti reale e immaginaria non possono essere raggruppate insieme, quindi un numero complesso avrà sempre una parte reale e una parte immaginaria..
Questa operazione estende l'insieme dei numeri reali al più ampio dei numeri complessi.
Applicazioni
Il nome dei numeri immaginari fu proposto dal matematico francese René Descartes (1596-1650) come presa in giro o disaccordo con la proposta degli stessi fatta dal matematico italiano del secolo Raffaelle Bombelli.
Altri grandi matematici, come Eulero e Leibniz, sostenevano Descartes in questo disaccordo e chiamavano numeri immaginari numeri anfibi, che erano combattuti tra l'essere e il niente.
Il nome dei numeri immaginari rimane ancora oggi, ma la loro esistenza e importanza è molto reale e palpabile, poiché compaiono naturalmente in molti campi della fisica come:
-La teoria della relatività.
-Nell'elettromagnetismo.
-Meccanica quantistica.
Esercizi con numeri immaginari
- Esercizio 1
Trova le soluzioni della seguente equazione:
zDue + 16 = 0
Soluzione
zDue = -16
Prendendo la radice quadrata in entrambi i membri abbiamo:
√ (zDue ) = √ (-16)
± z = √ (-1 x 16) = √ (-1) √ (16) = i x 4 = 4i
In altre parole, le soluzioni dell'equazione originale sono:
z = + 4i oppure z = -4i.
- Esercizio 2
Trova il risultato dell'innalzamento dell'unità immaginaria alla potenza 5 meno la sottrazione dell'unità immaginaria elevata alla potenza -5.
Soluzione
io5 - io-5 = i5 - 1 / i5 = i - 1 / i = i - (i) / (i x i) = i - i / (- 1) = i + i = 2i
- Esercizio 3
Trova il risultato della seguente operazione:
(3i)3 + 9i
Soluzione
33 io3 - 9 = 9 (-i) + 9i = -9i + 9i = 0i
- Esercizio 4
Trova le soluzioni della seguente equazione quadratica:
(-2x)Due + 2 = 0
Soluzione
L'equazione è riorganizzata come segue:
(-2x)Due = -2
Quindi viene presa la radice quadrata di entrambi i membri
√ ((- 2x)Due) = √ (-2)
± (-2x) = √ (-1 x 2) = √ (-1) √ (2) = i √ (2) = √2 io
Quindi risolviamo per x per ottenere finalmente:
x = ± √2 / 2 i
Cioè, ci sono due possibili soluzioni:
x = (√2 / 2) i
O quest'altro:
x = - (√2 / 2) i
- Esercizio 5
Trova il valore di Z definito da:
Z = √ (-9) √ (-4) + 7
Soluzione
Sappiamo che la radice quadrata di un numero reale negativo è un numero immaginario, ad esempio √ (-9) è uguale a √ (9) x √ (-1) = 3i.
D'altra parte, √ (-4) è uguale a √ (4) x √ (-1) = 2i.
Quindi l'equazione originale può essere sostituita da:
3i x 2i - 7 = 6 iDue - 7 = 6 (-1) - 7 = -6 - 7 = -13
- Esercizio 6
Trova il valore di Z risultante dalla seguente divisione di due numeri complessi:
Z = (9 - iDue) / (3 + i)
Soluzione
Il numeratore dell'espressione può essere scomposto utilizzando la seguente proprietà:
Una differenza di quadrati è il prodotto della somma e della differenza dei binomi senza quadrato.
Poi:
Z = [(3 - i) (3 + i)] / (3 + i)
L'espressione risultante viene quindi semplificata, lasciando
Z = (3 - i)
Riferimenti
- Earl, R. Numeri complessi. Estratto da: maths.ox.ac.uk.
- Figuera, J. 2000. Matematica 1st. Diversificato. Edizioni CO-BO.
- Hoffmann, J. 2005. Selezione di argomenti di matematica. Pubblicazioni Monfort.
- Jiménez, R. 2008. Algebra. Prentice Hall.
- Wikipedia. Numero immaginario. Estratto da: en.wikipedia.org



Nessun utente ha ancora commentato questo articolo.