Il numeri composti sono quei numeri interi che hanno più di due divisori. Se guardiamo da vicino, tutti i numeri sono almeno divisibili esattamente per se stessi e per 1. Quelli che hanno solo questi due divisori sono chiamati numeri primi e quelli che ne hanno di più sono composti..
Diamo un'occhiata al numero 2, che può essere diviso solo tra 1 e 2. Anche il numero 3 ha due divisori: 1 e 3. Pertanto, sono entrambi primi. Ora guardiamo il numero 12, che possiamo dividere esattamente per 2, 3, 4, 6 e 12. Avendo 5 divisori, 12 è un numero composto.
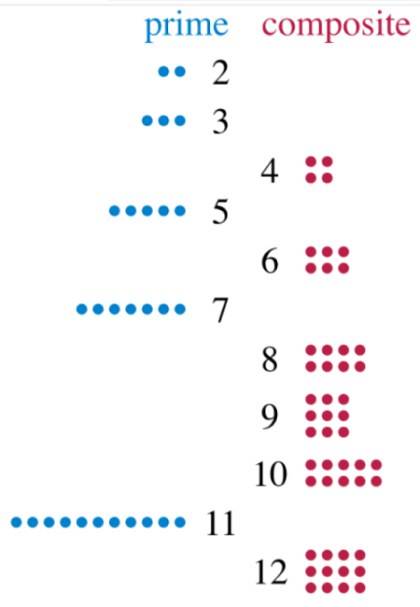
E cosa succede con il numero 1, quello che divide tutti gli altri? Ebbene, non è primo, perché non ha due divisori e non è composto, quindi 1 non rientra in nessuna di queste due categorie. Ma ci sono molti, molti altri numeri che lo fanno..
I numeri composti possono essere espressi come il prodotto di numeri primi e questo prodotto, ad eccezione dell'ordine dei fattori, è unico per ogni numero. Ciò è assicurato dal teorema fondamentale dell'aritmetica dimostrato dal matematico greco Euclide (325-365 a.C.).
Torniamo al numero 12, che possiamo esprimere in vari modi. Proviamone alcuni:
12 = 4 x 3 = 2 x 6 = 12 x 1 = 2Due x 3 = 3 x 2Due = 3 x 2 x 2 = 2 x 2 x 3 = 2 x 3 x 2
Le forme evidenziate in grassetto sono prodotti di numeri primi e l'unica cosa che cambia è l'ordine dei fattori, che sappiamo non altera il prodotto. Le altre forme, sebbene valide per esprimere 12, non sono costituite esclusivamente da numeri primi.
Se vogliamo scomporre un numero composto nei suoi fattori primi, dobbiamo dividerlo tra i numeri primi in modo che la divisione sia esatta, cioè che il resto sia 0.
Questa procedura è chiamata fattorizzazione in numeri primi o scomposizione canonica. I fattori primi possono essere elevati a esponenti positivi.
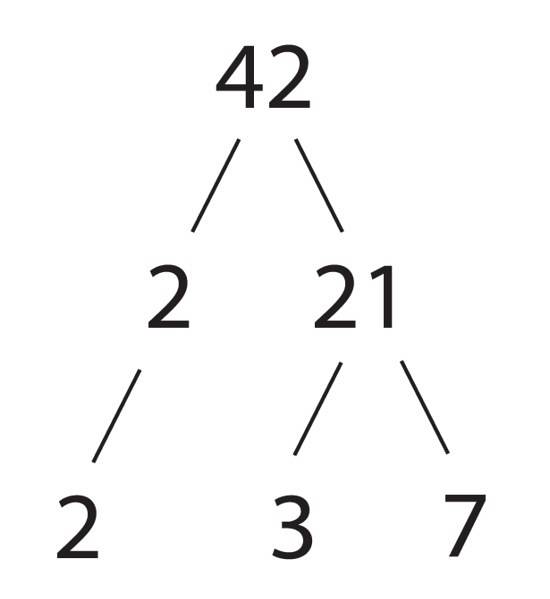
Andremo a scomporre il numero 570, notando che è pari e quindi divisibile per 2, che è un numero primo.
Useremo una barra per separare il numero a sinistra dai divisori a destra. I rispettivi quozienti vengono posti sotto il numero man mano che vengono ottenuti. La scomposizione è completa quando l'ultima cifra nella colonna di sinistra è 1:
570 │2
285 │
Quando si divide per 2 il quoziente è 285 che è divisibile per 5, un altro numero primo, che termina con 5.
570 │2
285 5
57 │
57 è divisibile per 3, anch'esso un primo, poiché la somma delle sue cifre 5 + 7 = 12 è un multiplo di 3.
570 │2
285 5
57 3
19 │
Infine otteniamo 19, che è un numero primo, i cui divisori sono 19 e 1:
570 │2
285 5
57 3
19-19
1 │
Ottenendo 1 possiamo già esprimere 570 in questo modo:
570 = 2 x 5 x 3 x 19
E vediamo che in effetti è il prodotto di 4 numeri primi.
In questo esempio iniziamo dividendo per 2, ma gli stessi fattori (in un altro ordine) sarebbero stati ottenuti se iniziassimo dividendo per 5, ad esempio.
Per scomporre un numero composto nei suoi fattori primi, è necessario dividerlo esattamente. I criteri di divisibilità tra numeri primi sono regole che consentono di sapere quando un numero è divisibile esattamente per un altro, senza dover provare o provare.
Tutti i numeri pari, quelli che terminano con 0 o un numero pari sono divisibili per 2.
Se la somma delle cifre di un numero è un multiplo di 3, anche il numero è divisibile per 3.
I numeri che terminano con 0 o 5 sono divisibili per 5.
Un numero è divisibile per 7 se separando l'ultima cifra, moltiplicandola per 2 e sottraendo il numero rimanente, il valore risultante è un multiplo di 7.
Questa regola sembra un po 'più complicata delle precedenti, ma in realtà non è poi così tanto, quindi facciamo un esempio: 98 sarà divisibile per 7?
Seguiamo le istruzioni: separiamo l'ultima cifra che è 8, la moltiplichiamo per 2 che dà 16. Il numero che rimane quando separiamo l'8 è 9. Sottraiamo 16 - 9 = 7. E poiché 7 è un multiplo di se stesso , 98 è divisibile tra 7.
Se la somma delle cifre in posizione pari (2, 4, 6 ...) viene sottratta dalla somma delle cifre in posizione dispari (1, 3, 5, 7 ...) e si ottiene 0 o un multiplo di 11, il numero è divisibile per 11.
I primi multipli di 11 sono facilmente identificabili: sono 11, 22, 33, 44… 99. Ma attenzione, 111 non è, invece 110 è.
Ad esempio, vediamo se 143 è un multiplo di 11.
Questo numero ha 3 cifre, l'unica cifra pari è 4 (la seconda), le due cifre dispari sono 1 e 3 (prima e terza) e la loro somma è 4.
Entrambe le somme vengono sottratte: 4-4 = 0 e poiché si ottiene 0 risulta che 143 è un multiplo di 11.
Il numero senza la cifra delle unità deve essere sottratto da 9 volte quella cifra. Se il conteggio restituisce 0 o un multiplo di 13, il numero è un multiplo di 13.
Ad esempio, verificheremo che 156 è un multiplo di 13. La cifra delle unità è 6 e il numero che rimane senza è 15. Moltiplichiamo 6 x 9 = 54 e ora sottraiamo 54 - 15 = 39.
Ma 39 è 3 x 13, quindi 56 è un multiplo di 13.
Due o più numeri primi o composti possono essere primi o co-primi. Ciò significa che l'unico divisore comune che hanno è 1.
Ci sono due proprietà importanti da ricordare quando si tratta di coprimi:
-Due, tre e più numeri consecutivi sono sempre primi tra loro.
-Lo stesso si può dire per due, tre o più numeri dispari consecutivi.
Ad esempio 15, 16 e 17 sono numeri primi tra loro e quindi sono 15, 17 e 19.
Un numero primo ha due divisori, lo stesso numero e 1. E quanti divisori ha un numero composto? Questi possono essere cugini o composti.
Sia N un numero composto espresso in termini della sua scomposizione canonica come segue:
N = an . bm. cp... rK
Dove a, b, c… r sono i fattori primi e n, m, p… k i rispettivi esponenti. Ebbene, il numero di divisori C che ha N è dato da:
C = (n +1) (m + 1) (p +1)… (k + 1)
Con C = divisori primi + divisori composti + 1
Ad esempio 570, che è espresso in questo modo:
570 = 2 x 5 x 3 x 19
Tutti i fattori primi vengono portati a 1, quindi 570 ha:
C = (1 + 1) (1 + 1) (1+ 1) (1 +1) = 16 divisori
Di questi 10 divisori che già conosciamo: 1, 2, 3, 5, 19 e 570. Mancano altri 10 divisori, che sono numeri composti: 6, 10, 15, 30, 38, 57, 95, 114, 190 e 285. Si trovano osservando la scomposizione in fattori primi e moltiplicando anche combinazioni di questi fattori insieme..
Decomponi i seguenti numeri in fattori primi:
a) 98
b) 143
c) 540
d) 3705
98 │2
49 │7
7 │7
1 │
98 = 2 x 7 x 7
143 11
13-13
1 │
143 = 11 x 13
540 │5
108 │2
54 │2
27 │3
9 │3
3 │3
1 │
540 = 5 x 2 x 2 x 3 x 3 x 3 = 5 x 2Due x 33
3705 5
741 │3
247 13
19-19
1 │
3705 = 5 x 3 x 13 x 19
Scopri se i seguenti numeri sono primi tra loro:
6, 14, 9
-I divisori di 6 sono: 1, 2, 3, 6
-Per quanto riguarda il 14, è divisibile per: 1, 2, 7, 14
-Infine 9 ha come divisori: 1, 3, 9
L'unico divisore che hanno in comune è 1, quindi sono primi l'uno per l'altro.
Nessun utente ha ancora commentato questo articolo.