
Proprietà dei numeri complessi, esempi, operazioni
Il numeri complessi sono l'insieme numerico che include i numeri reali e tutte le radici dei polinomi, comprese le radici pari dei numeri negativi. Queste radici non esistono nell'insieme dei numeri reali, ma nei numeri complessi c'è la soluzione.
Un numero complesso è costituito da una parte reale e da una parte chiamata "immaginaria". La parte reale si chiama per, per esempio, e la parte immaginaria ib, con per Y b numeri reali e "i" come unità immaginaria. In questo modo il numero complesso assume la forma:
z = a + ib

Esempi di numeri complessi sono 2 - 3i, -πi, 1 + (1/2) i. Ma prima di operare con loro, vediamo da dove ha origine l'unità immaginaria io, considerando questa equazione quadratica:
XDue - 10x + 34 = 0
In cui a = 1, b = -10 ec = 34.
Quando si applica la formula risolutiva per determinare la soluzione, troviamo quanto segue:

Come determinare il valore di √-36? Non esiste un numero reale che al quadrato dia come risultato una quantità negativa. Quindi si conclude che questa equazione non ha soluzioni reali.
Tuttavia, possiamo scrivere questo:
√-36 = √-6Due = √6Due (-1) = 6√-1
Se definiamo un certo valore X tale che:
XDue = -1
Poi:
x = ± √-1
E l'equazione di cui sopra avrebbe una soluzione. Pertanto, l'unità immaginaria è stata definita come:
io = √-1
E così:
√-36 = 6i
Molti matematici dell'antichità hanno lavorato per risolvere problemi simili, in particolare il rinascimentale Girolamo Cardano (1501-1576), Nicolo Fontana (1501-1557) e Raffaele Bombelli (1526-1572).
Anni dopo René Descartes (1596-1650) chiamò quantità come √-36 nell'esempio "immaginario". Per questo motivo √-1 è noto come unità immaginaria.
Indice articolo
- 1 Proprietà dei numeri complessi
- 2 Rappresentazione di numeri complessi
- 2.1 - Forma binomiale
- 2.2 - Forma polare
- 3 Esempi di numeri complessi
- 4 A cosa servono?
- 5 Operazioni con numeri complessi
- 5.1 - Esempio 1
- 5.2 - Esempio 2
- 6 Applicazione
- 7 Riferimenti
Proprietà dei numeri complessi
-L'insieme dei numeri complessi è indicato con C e include i numeri reali R e i numeri immaginari Im. I set di numeri sono rappresentati in un diagramma di Venn, come mostrato nella figura seguente:
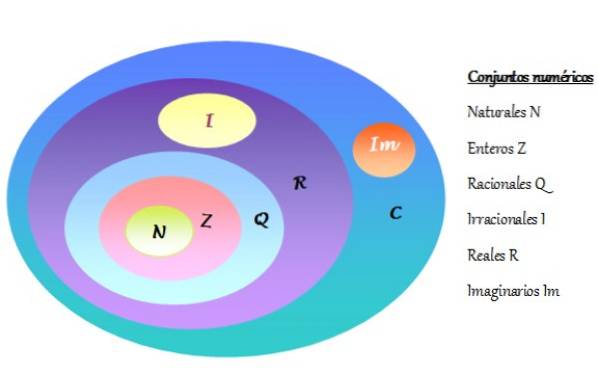
-Ogni numero complesso è costituito da una parte reale e da una parte immaginaria.
-Quando la parte immaginaria di un numero complesso è 0, è un numero reale puro.
-Se la parte reale di un numero complesso è 0, il numero è puro immaginario.
-Due numeri complessi sono uguali se la rispettiva parte reale e la parte immaginaria sono uguali.
-Con i numeri complessi, vengono eseguite le operazioni note di addizione, sottrazione, moltiplicazione, prodotto e miglioramento, risultando in un altro numero complesso.
Rappresentazione di numeri complessi
I numeri complessi possono essere rappresentati in vari modi. Ecco i principali:
- Forma binomiale
È la forma data all'inizio, dove z è il numero complesso, per è la parte reale, b è la parte immaginaria e io è l'unità immaginaria:
z = a + ib
O anche:
z = x + iy
Un modo per rappresentare graficamente il numero complesso è attraverso il piano complesso mostrato in questa figura. L'asse immaginario Im è verticale, mentre l'asse reale è orizzontale ed è indicato come Re.
Il numero complesso z è rappresentato su questo piano come un punto di coordinate (x, y) o (a, b), come si fa con i punti del piano reale.
La distanza dall'origine al punto z è il modulo del numero complesso, indicato come r, mentre φ è l'angolo che si forma r con l'asse reale.
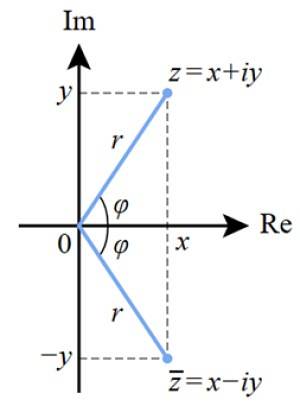
Questa rappresentazione è strettamente correlata a quella dei vettori nel piano reale. Il valore di r corrisponde a modulo del numero complesso.
- Forma polare
La forma polare consiste nell'esprimere il numero complesso fornendo i valori di r e di φ. Se guardiamo la figura, il valore di r corrisponde all'ipotenusa di un triangolo rettangolo. Le gambe valgono per Y b, Oh bene X Y Y.
Dalla forma binomiale o binomiale, possiamo passare alla forma polare:
r = √xDue+YDue
L'angolo φ È quello che forma il segmento r con l'asse orizzontale o l'asse immaginario. È noto come discussione del numero complesso. In questo modo:
φ = arctg (y / x)
L'argomento ha valori infiniti, tenendo conto che ogni volta che si gira una svolta, che vale 2π radianti, r occupa nuovamente la stessa posizione. In questo modo generale, l'argomento di z, indicato con Arg (z), è espresso in questo modo:
Arg (z) = φ + 2kπ
Dove k è un numero intero e viene utilizzato per indicare il numero di giri girati: 2, 3, 4…. Il segno indica il senso di rotazione, se è in senso orario o antiorario.
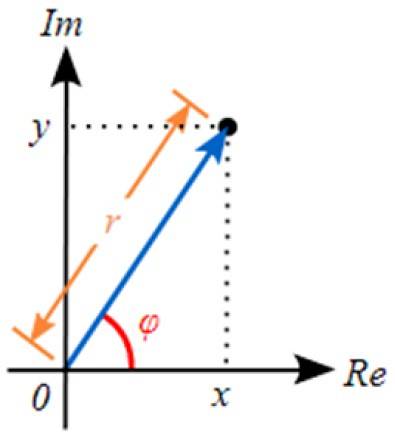
E se vogliamo passare dalla forma polare alla forma binomiale, usiamo i rapporti trigonometrici. Dalla figura precedente possiamo vedere che:
x = r cos φ
y = r sin φ
In questo modo z = r (cos φ + i sin φ)
Che è abbreviato in questo modo:
z = r cis φ
Esempi di numeri complessi
I seguenti numeri complessi sono forniti in forma binomiale:
a) 3 + i
b) 4
d) -6i
E questi sotto forma di una coppia ordinata:
a) (-5, -3)
b) (0, 9)
c) (7.0)
Infine, questo gruppo è dato in forma polare o trigonometrica:
a) √2 cis 45º
b) √3 cis 30º
c) 2 cis 315º
A cosa servono?
L'utilità dei numeri complessi va oltre la risoluzione dell'equazione quadratica mostrata all'inizio, poiché sono essenziali nel campo dell'ingegneria e della fisica, soprattutto in:
-Lo studio delle onde elettromagnetiche
-Analisi della corrente alternata e della tensione
-Modellazione di tutti i tipi di segnali
-Teoria della relatività, dove si presume che il tempo sia una grandezza immaginaria.
Operazioni con numeri complessi
Con i numeri complessi possiamo eseguire tutte le operazioni che si fanno con quelli reali. Alcuni sono più facili da fare se i numeri sono in forma binomiale, come addizione e sottrazione. Invece, la moltiplicazione e la divisione sono più semplici se vengono eseguite con la forma polare.
Diamo un'occhiata ad alcuni esempi:
- Esempio 1
Aggiungi z1 = 2 + 5i e zDue = -3 -8i
Soluzione
Le parti reali vengono aggiunte separatamente dalle parti immaginarie:
z1 + zDue = (2 + 5i) + (-3 -8i) = -1 -3i
- Esempio 2
Moltiplica z1 = 4 cis 45º e zDue = 5 cis 120º
Soluzione
Si può dimostrare che il prodotto di due numeri complessi in forma polare o trigonometrica è dato da:
z1 . zDue = r1.rDue cis (φ1 + φDue)
Secondo questo:
z1 . zDue = (4 × 5) cis (45 + 120) = 20 cis 165º
App
Una semplice applicazione di numeri complessi è trovare tutte le radici di un'equazione polinomiale come quella mostrata all'inizio dell'articolo.
Nel caso dell'equazione xDue - 10x + 34 = 0, applicando la formula risolutiva otteniamo:

Pertanto le soluzioni sono:
X1 = 5 + 3i
XDue = 5 - 3i
Riferimenti
- Earl, R. Numeri complessi. Estratto da: maths.ox.ac.uk.
- Figuera, J. 2000. Matematica 1st. Diversificato. Edizioni CO-BO.
- Hoffmann, J. 2005. Selezione di argomenti di matematica. Pubblicazioni Monfort.
- Jiménez, R. 2008. Algebra. Prentice Hall.
- Wikipedia. Numeri complessi. Estratto da: en.wikipedia.org


Nessun utente ha ancora commentato questo articolo.