
Definizione e caratteristiche degli angoli nulli, esempi, esercizi
Il angolo nullo È uno la cui misura è 0, sia in gradi che in radianti o un altro sistema di misurazione dell'angolo. Pertanto, manca di larghezza o apertura, come quella formata tra due linee parallele..
Sebbene la sua definizione sembri abbastanza semplice, l'angolo nullo è molto utile in molte applicazioni di fisica e ingegneria, nonché nella navigazione e nella progettazione..
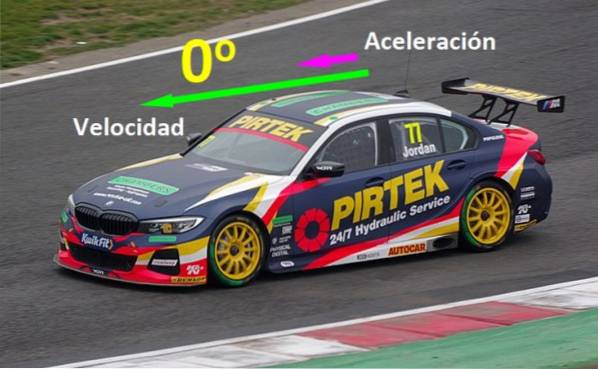
Ci sono quantità fisiche che devono essere allineate parallelamente per ottenere determinati effetti: se un'auto si muove in linea retta su un'autostrada e inserisci il suo vettore di velocità v e il suo vettore di accelerazione per c'è 0º, l'auto si muove sempre più velocemente, ma se l'auto frena, la sua accelerazione è opposta alla sua velocità (vedi figura 1).
La figura seguente mostra diversi tipi di angolo compreso l'angolo nullo a destra. Come si può vedere, l'angolo 0º manca di larghezza o apertura..

Indice articolo
- 1 Esempi di angoli nulli
- 1.1 - Effetti dell'angolo nullo sulle grandezze fisiche
- 2 esercizi
- 2.1 - Esercizio 1
- 2.2 - Esercizio 2
- 3 Riferimenti
Esempi di angoli nulli
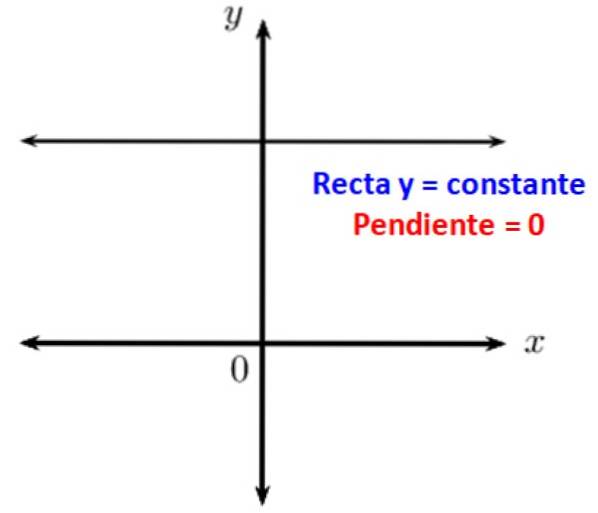
È noto che le linee parallele formano un angolo zero l'una con l'altra. Quando hai una linea orizzontale, è parallela all'asse x del sistema di coordinate cartesiane, quindi la sua inclinazione rispetto ad essa è 0. In altre parole, le linee orizzontali hanno pendenza zero.
Anche i rapporti trigonometrici dell'angolo nullo sono 0, 1 o infinito. Pertanto l'angolo nullo è presente in molte situazioni fisiche che implicano operazioni con vettori. Questi motivi sono:
-sin 0º = 0
-cos 0º = 1
-tg 0º = 0
-sec 0º = 1
-cosec 0º → ∞
-ctg 0º → ∞
E serviranno per analizzare alcuni esempi di situazioni in cui la presenza dell'angolo nullo gioca un ruolo fondamentale:
- Effetti dell'angolo nullo sulle grandezze fisiche
Aggiunta di vettore
Quando due vettori sono paralleli, l'angolo tra di loro è zero, come mostrato nella Figura 4a sopra. In questo caso la somma di entrambi si effettua sovrapponendola e l'ampiezza del vettore somma è la somma delle grandezze degli addendi (figura 4b).

Quando due vettori sono paralleli, l'angolo tra di loro è zero, come mostrato nella Figura 4a sopra. In questo caso la somma di entrambi si effettua sovrapponendola e l'ampiezza del vettore somma è la somma delle grandezze degli addendi (figura 4b)
La coppia o coppia
La coppia o coppia provoca la rotazione di un corpo. Dipende dall'entità della forza applicata e da come viene applicata. Un esempio molto rappresentativo è la chiave nella figura.
Per ottenere il miglior effetto di rotazione, la forza viene applicata perpendicolarmente all'impugnatura della chiave, verso l'alto o verso il basso, ma non è prevista alcuna rotazione se la forza è parallela all'impugnatura..
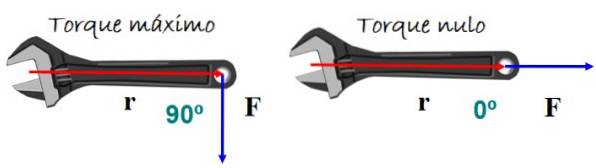
Matematicamente coppia τ è definito come prodotto incrociato o prodotto incrociato tra vettori r (vettore di posizione) e F (vettore forza) dalla figura 5:
τ = r X F
L'entità della coppia è:
τ = r F sin θ
Dove θ è l'angolo tra r Y F. Quando sin θ = 0 la coppia è zero, in questo caso θ = 0º (o anche 180º).
Flusso di campo elettrico
Il flusso del campo elettrico è una grandezza scalare che dipende dall'intensità del campo elettrico e dall'orientamento della superficie attraverso la quale passa..
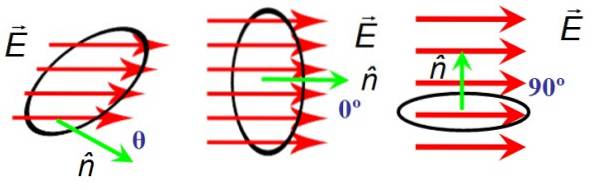
Nella figura 6 è presente una superficie circolare dell'area A attraverso la quale passano le linee del campo elettrico E. L'orientamento della superficie è dato dal vettore normale n. A sinistra il campo e il vettore normale formano un angolo acuto arbitrario θ, al centro formano un angolo nullo tra loro ea destra sono perpendicolari.
quando E Y n sono perpendicolari, le linee di campo non attraversano la superficie e quindi il flusso è nullo, mentre quando l'angolo tra E Y n è nullo, le linee attraversano completamente la superficie.
Denotando il flusso del campo elettrico con la lettera greca Φ (leggi "fi"), la sua definizione di campo uniforme come nella figura, ha questo aspetto:
Φ = E•nPER
Il punto al centro di entrambi i vettori denota il prodotto scalare o il prodotto scalare, che in alternativa è definito come segue:
Φ = E•nA = EAcosθ
Il grassetto e le frecce sopra la lettera sono risorse per distinguere tra un vettore e la sua grandezza, che è indicata da lettere normali. Poiché cos 0 = 1, il flusso è massimo quando E Y n sono paralleli.
Formazione
- Esercizio 1
Due forze P Y Q agiscono simultaneamente su un oggetto punto X, entrambe le forze formano inizialmente un angolo θ tra di loro. Cosa succede all'entità della forza risultante quando θ diminuisce a zero?
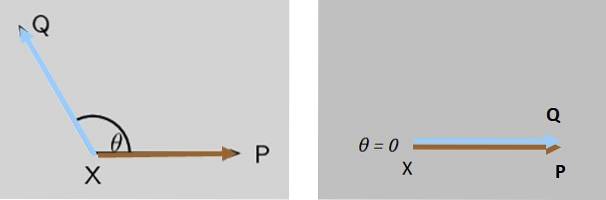
Soluzione
L'entità della forza risultante Q + P aumenta gradualmente fino a raggiungere il massimo quando Q Y P sono totalmente parallele (figura 7 a destra).
- Esercizio 2
Indicare se l'angolo nullo è una soluzione della seguente equazione trigonometrica:
cos 2x = 1 + 4 sin x
Soluzione
Un'equazione trigonometrica è quella in cui l'ignoto è parte dell'argomento di un rapporto trigonometrico. Per risolvere l'equazione proposta, è conveniente utilizzare la formula per il coseno del doppio angolo:
cos 2x = cosDue x - peccatoDue X
Perché in questo modo l'argomento a sinistra diventa X invece di 2x. Poi:
cosDue x - peccatoDue x = 1 + 4sin x
D'altra parte cosDue x + peccatoDue x = 1, quindi:
cosDue x - peccatoDue x = cosDue x + peccatoDue x + 4sen x
Il termine cosDue x viene cancellato e rimane:
- senDue x = peccatoDue x + 4sen x → - 2senDue x - 4senx = 0 → 2senDue x + 4senx = 0
Ora viene apportata la seguente modifica alla variabile: sinx = u e l'equazione diventa:
2uDue + 4u = 0
2u (u + 4) = 0
Le cui soluzioni sono: u = 0 eu = -4. Restituendo la modifica avremmo due possibilità: sin x = 0 e sinx = -4. Quest'ultima soluzione non è praticabile, perché il seno di qualsiasi angolo è compreso tra -1 e 1, quindi ci resta la prima alternativa:
sin x = 0
Quindi x = 0º è una soluzione, ma funziona anche qualsiasi angolo il cui seno è 0, che può anche essere 180º (π radianti), 360º (2 π radianti) e anche i rispettivi negativi.
La soluzione più generale dell'equazione trigonometrica è: x = kπ dove k = 0, ± 1, ± 2, ± 3,…. k un numero intero.
Riferimenti
- Baldor, A. 2004. Geometria del piano e dello spazio con la trigonometria. Publicaciones Cultural S.A. de C.V. Messico.
- Figueroa, D. (2005). Serie: Fisica per la scienza e l'ingegneria. Volume 3. Sistemi di particelle. A cura di Douglas Figueroa (USB).
- Figueroa, D. (2005). Serie: Fisica per la scienza e l'ingegneria. Volume 5. Interazione elettrica. A cura di Douglas Figueroa (USB).
- OnlineMathLearning. Tipi di angoli. Estratto da: onlinemathlearning.com.
- Zill, D. 2012. Algebra, trigonometria e geometria analitica. McGraw Hill Interamericana.



Nessun utente ha ancora commentato questo articolo.