
Doppio campionamento


Cos'è il doppio campionamento?
Il doppio campionamento è una tecnica utilizzata nelle statistiche inferenziali quando si desidera conoscere maggiori dettagli e certezza su una particolare variabile, che caratterizza una determinata popolazione.
Il secondo campione di popolazione viene generalmente effettuato dopo che un primo campione è stato prelevato e analizzato, la cui analisi non ha prodotto una conclusione statisticamente significativa su nessuna delle variabili di studio..
Per questo motivo, il doppio campionamento in statistica è anche noto come campionamento in due fasi. L'utilità del secondo campione è quella di aiutare a determinare con maggiore precisione la stima dei rapporti e delle regressioni di una certa variabile ausiliaria, che emerge alla luce dell'analisi di un primo campione..
Un altro uso che viene dato al doppio campionamento è quello di raccogliere informazioni per effettuare un campionamento per strati..
Esempi
Di seguito verranno descritte varie situazioni in cui è garantito il doppio campionamento..
Controllo di qualità nella produzione di parti
Il metodo del doppio campionamento è spesso utilizzato nel controllo della qualità industriale e di solito viene eseguito in due fasi..
Ad esempio, supponiamo una macchina industriale che produce determinate parti. Non importa quanto sia regolata la macchina, nessuna parte è identica a un'altra, poiché possono verificarsi piccole variazioni nelle sue dimensioni e nel suo peso. Si tratta di determinare se un lotto di parti prodotte da detta macchina soddisfa i criteri di tolleranza per essere accettato o rifiutato..
Per prima cosa viene prelevato un campione casuale di pezzi con il quale si vuole verificare se una delle variabili, ad esempio la lunghezza del pezzo, rientra nella tolleranza.
Nel caso in cui la lunghezza media sia inferiore o superiore al grado di tolleranza desiderato per detta variabile, in questo primo campione, si deduce quindi che il lotto è difettoso e deve essere scartato. In questo caso non sono necessari nuovi campioni.
Al contrario, se il valore medio rientra nell'intervallo di tolleranza, ma la deviazione standard del campione è abbastanza grande da far sì che l'addizione o la sottrazione del valore medio non rientri nell'intervallo, sarà necessario raccogliere un secondo campione più grande..
Questo secondo campione deve includere il campione originale per rifare i calcoli e quindi essere in grado di prendere una decisione finale riguardo alla variabile investigata. In questo modo è possibile sapere se il lotto è difettoso o meno.
Costi di campionamento inferiori
In molte occasioni, è difficile accedere alle informazioni su una delle variabili da studiare. Ma potrebbe esserci una variabile ausiliaria più facilmente per la raccolta dei dati.
In questo caso vengono prelevati due campioni, uno grande per la variabile ausiliaria, meno costosa, e un campione più piccolo, contenuto nel campione più grande della variabile più costosa..
Questo metodo è applicabile ogni volta che si determina che esiste una correlazione tra entrambe le variabili, che generalmente è una relazione proporzionale..
Un esempio di questa situazione appare nelle scienze forestali, dove si desidera determinare la percentuale di alberi colpiti da una pianta parassita (tigna).
Trattandosi di regioni molto estese e di difficile accesso, lo studio dell'intera popolazione di alberi non è fattibile in tempi e costi. Questi passaggi vengono quindi seguiti:
Passaggio 1: prelievo di campioni
Un campionamento preliminare consisterebbe nell'utilizzo della fotografia aerea e il bosco è suddiviso in lotti. Da qui vengono scelti casualmente alcuni lotti e si stima, analizzando le immagini dei lotti scelti, quanti alberi sono affetti dalla tigna, poiché il colore degli alberi è influenzato dal parassita..
Passaggio 2: lavoro sul campo
Ma l'analisi fotografica può essere imprecisa, quindi vengono scelti alcuni lotti del primo campione, preferibilmente a caso, per svolgere il lavoro sul campo..
Passaggio 3: confronto
Il risultato di campo viene poi confrontato con quello fotografico per l'intercettazione delle due serie di lotti. Questo confronto può essere effettuato, ad esempio, realizzando un grafico in cui l'asse orizzontale è il valore ottenuto per ogni lotto tramite fotografia e sull'asse verticale il valore ottenuto per lotto tramite il lavoro sul campo..
Questo metodo grafico consente di identificare visivamente se esiste o meno una correlazione tra i due risultati e di determinare, tramite un'analisi di regressione, il coefficiente di proporzionalità o rapporto tra i due campioni..
Dopo il campione più grande, ovvero il campione fotografico, vengono presi il valore medio degli alberi infetti e la loro deviazione standard. Ma poiché sono stati determinati il coefficiente di proporzionalità e il suo errore con i campioni di campo, è possibile correggere il risultato del campione più grande (quello fotografico).
Questo risultato può quindi essere estrapolato all'intera popolazione di alberi.
Vantaggi e svantaggi del doppio campionamento
Negli esempi descritti è evidente il vantaggio in termini di costo, poiché sostituire una variabile facilmente accessibile con un'altra di difficile accesso fa risparmiare tempo e denaro..
Uno svantaggio è che, in caso di doppio campionamento per il controllo di qualità, c'è il rischio di passare attraverso buoni lotti di prodotti fuori tolleranza..
Esercizio
Vogliamo stimare il numero di alberi malati in una foresta di 162 ettari. Poiché la foresta è molto estesa, è suddivisa in 100 parcelle della stessa area. 18 parcelle vengono scelte casualmente e tramite uno studio fotografico si stima che in queste 18 parcelle ci siano 8,5 alberi malati con un errore standard di più o meno 4,5 alberi.
Da questi 18 grafici, vengono scelti a caso 8 grafici in cui viene condotto lo studio sul campo. Per questi otto lotti, lo studio fotografico mostra 10 alberi malati con un errore di più o meno 5,3 alberi..
D'altra parte, per quegli stessi otto grafici lo studio sul campo mostra 12,4 alberi malati con un errore di più meno 6,3 alberi.
Chiede:
- a) Determinare il coefficiente di proporzionalità tra lo studio sul campo mediante regressione lineare.
- b) Stimare il numero di alberi malati utilizzando il metodo fotografico nelle centinaia di parcelle.
- c) Applicare la correzione con il coefficiente di proporzionalità ottenuto, per stimare il numero reale di alberi malati nell'intera foresta.
Soluzione
Viene creato un grafico del numero di alberi per conteggio fotografico rispetto al conteggio dei campi per gli otto lotti selezionati per entrambi gli studi..
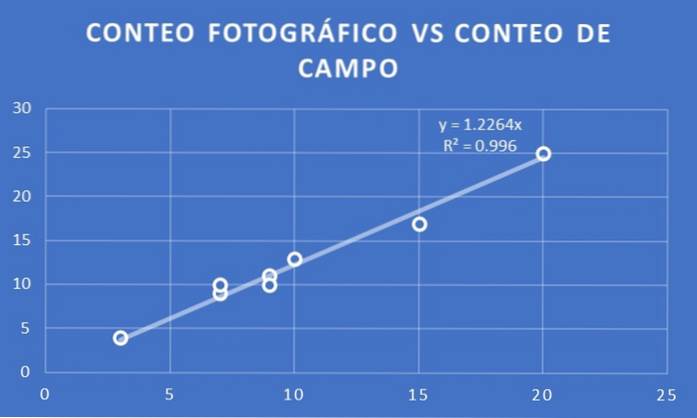
Viene adattata una linea di tendenza e viene determinata la sua pendenza. In questo caso si ottiene che il coefficiente di proporzionalità è 1,23. Cioè, se X è il numero per conteggio fotografico, si stima che il conteggio del campo sarà Y = 1,23 X.
Il numero di alberi malati secondo il conteggio fotografico nei 18 lotti selezionati sarà:
18 x 8,5 = 153
Ma poiché l'intera foresta era divisa in 100 appezzamenti della stessa area, il numero di alberi malati stimato con il metodo fotografico è: (100/18) x 153 = 850.
Viene ora applicato il fattore di correzione ottenuto dal confronto tra il campo e lo studio fotografico:
Numero effettivo stimato di alberi malati nella foresta = 1,23 x 850 = 1046.
Riferimenti
- Doppio campionamento per la stima del rapporto, PennState College. Recuperato da psu.edu
- Campionamento doppio, multiplo e sequenziale, NC State University. Recupero da ncsu.edu
- Campionamento casuale semplice. Recuperato da investopedia.com
- Cos'è il doppio campionamento? Estratto da: nist.gov
- Campionamento. Estratto da: en.wikipedia.org
- Campionamento multistadio. Estratto da: en.wikipedia.org


Nessun utente ha ancora commentato questo articolo.