Caratteristiche del moto rettilineo uniformemente accelerato, formule

Il moto rettilineo uniformemente accelerato È uno che corre lungo una linea retta e in cui il cellulare aumenta o diminuisce la sua velocità a una velocità costante. Questa velocità è la grandezza che descrive la velocità con cui la velocità cambia e viene chiamata accelerazione.

Nel caso di moto rettilineo uniformemente accelerato o variato (MRUV), l'accelerazione costante è responsabile della variazione della grandezza della velocità. In altri tipi di movimento, l'accelerazione è anche in grado di cambiare la direzione e il senso della velocità, o anche solo di cambiare direzione, come nel movimento circolare uniforme..

Poiché l'accelerazione rappresenta il cambiamento di velocità nel tempo, le sue unità nel Sistema Internazionale sono m / s^Due (metri su secondi quadrati). Come la velocità, all'accelerazione può essere assegnato un segno positivo o negativo, a seconda che la velocità aumenti o diminuisca..

Un'accelerazione di diciamo +3 m / s^Due significa che per ogni secondo che passa, la velocità del cellulare aumenta di 3 m / s. Se all'inizio del movimento (at = 0) la velocità del mobile era +1 m / s, dopo un secondo sarà 4 m / se dopo 2 secondi sarà 7 m / s.

Nel movimento rettilineo uniformemente variato, vengono prese in considerazione le variazioni di velocità che gli oggetti in movimento subiscono quotidianamente. Questo è un modello più realistico rispetto al moto rettilineo uniforme. Anche così, è ancora piuttosto limitato, poiché limita il cellulare a viaggiare solo su una linea retta.

Indice articolo

• 1 Caratteristiche
  • 1.1 Distanza percorsa dal grafico v vs. t
• 2 Formule ed equazioni
• 3 esercizi risolti
  • 3.1 -Esercizio risolto 1
  • 3.2 -Esercizio risolto 2
• 4 Applicazioni
• 5 Riferimenti

Caratteristiche

Queste sono le principali caratteristiche del moto rettilineo uniformemente accelerato:

-Il movimento scorre sempre lungo una linea retta.

-L'accelerazione del cellulare è costante, sia in grandezza che in direzione e senso.

-La velocità del dispositivo mobile aumenta (o diminuisce) in modo lineare.

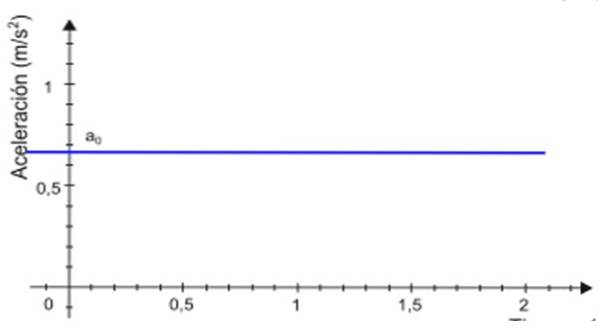
-Dall'accelerazione per rimane costante nel tempo t, il grafico della sua grandezza in funzione del tempo è una linea retta. Nell'esempio mostrato in figura 2, la linea è colorata di blu e il valore dell'accelerazione viene letto sull'asse verticale, circa +0,68 m / s^Due.

-Il grafico della velocità v di t è una linea retta (in verde in figura 3), la cui pendenza è uguale all'accelerazione del mobile. Nell'esempio la pendenza è positiva.

-Il taglio con l'asse verticale indica la velocità iniziale, in questo caso è di 0,4 m / s.

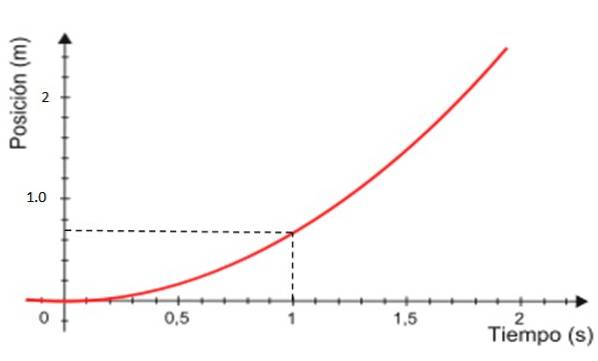
-Infine il grafico della posizione x rispetto al tempo è la curva mostrata in rosso nella figura 4, che è sempre una parabola.

Distanza percorsa dal grafico v vs. t

Avendo il grafico v vs. t, calcolare la distanza percorsa dal cellulare è molto semplice. La distanza percorsa è uguale all'area sotto la linea che si trova nell'intervallo di tempo desiderato.

Nell'esempio mostrato, supponiamo di voler conoscere la distanza percorsa dal cellulare tra 0 e 1 secondo. Utilizzando questo grafico, vedere la Figura 5.

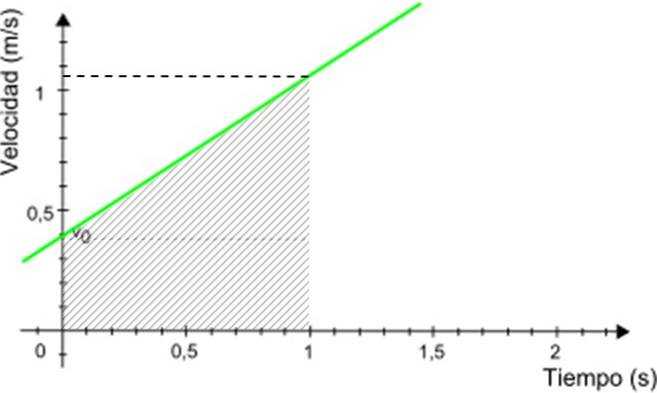
La distanza ricercata è numericamente equivalente all'area del trapezio ombreggiato in figura 3. L'area del trapezio è data da: (base maggiore + base minore) x altezza / 2

Distanza percorsa = (0,4 + 1,05) x 1/2 m = 0,725 m

È anche possibile dividere l'area ombreggiata in un triangolo e un rettangolo, calcolare le aree corrispondenti e sommarle. La distanza percorsa è positiva, anche se la particella va a destra oa sinistra.

Formule ed equazioni

Sia l'accelerazione media che l'accelerazione istantanea hanno lo stesso valore nell'MRUV, quindi:

-Accelerazione: per = costante

Quando l'accelerazione è uguale a 0 il movimento è rettilineo uniforme, poiché in questo caso la velocità sarebbe costante. Il segno di per Può essere positivo o negativo.

Poiché l'accelerazione è la pendenza della retta v rispetto a t, l'equazione v (t) è:

-Velocità in funzione del tempo: v (t) = v_o + a

Dove v_o è il valore della velocità iniziale del cellulare

-Posizione in funzione del tempo: x (t) = x_o + v_o t + ½at^Due 

Quando non hai tempo, ma invece hai velocità e spostamenti, c'è un'equazione molto utile che si ottiene risolvendo il tempo di v (t) = v_o + a e sostituendolo nell'ultima equazione. Riguarda:

-Equazione che non contiene tempo: v^Due = v_o^Due +2.a.ΔX

Esercizi risolti

Quando si risolve un esercizio di cinematica, è importante assicurarsi che la situazione sia adattata al modello da utilizzare. Ad esempio le equazioni del moto rettilineo uniforme non sono valide per il moto accelerato.

E quelli del movimento accelerato non sono validi per un movimento circolare o curvilineo, ad esempio. Il primo di questi esercizi risolto di seguito combina due cellulari con movimenti diversi. Per risolverlo correttamente, è necessario andare al modello di movimento appropriato.

-Risolto esercizio 1

Per scoprire la profondità di un pozzo, un bambino lascia cadere una moneta e contemporaneamente attiva il suo timer, che si ferma subito dopo aver sentito la moneta colpire l'acqua. La sua lettura era di 2,5 secondi. Sapendo che la velocità del suono nell'aria è di 340 m / s, calcola la profondità del pozzo.

Soluzione

Essere h la profondità del pozzo. La moneta percorre questa distanza in caduta libera, un movimento verticale uniformemente variato, con velocità iniziale 0, al momento della caduta della moneta, e accelerazione costante verso il basso pari a 9,8 m / s^Due. Prendi tempo t_m in questo modo.

Una volta che la moneta colpisce l'acqua, il suono causato dal clic viaggia verso l'alto fino all'orecchio del bambino, che ferma il cronometro quando lo sente. Non c'è motivo di credere che la velocità del suono cambi mentre sale nel pozzo, quindi il movimento del suono è rettilineo uniforme. Il suono richiede un po 'di tempo t_S per arrivare al bambino.

Equazione del moto per la moneta:

h = ½.g.t_m ^Due = 4,9 t_m ^Due

Dove sono stati sostituiti X Y per dell'equazione per la posizione data nella sezione precedente, da h Y g.

Equazione del moto per il suono:

h = v_S . t_S = 340 t_S

Si tratta dell'equazione familiare distanza = velocità x tempo. Con queste due equazioni abbiamo tre incognite: h, tm e ts. Per le volte che c'è una relazione, è noto che tutto impiega 2,5 secondi per accadere, quindi:

t_m + t_S = 2,5 s

Equalizzazione di entrambe le equazioni:

4,9 t_m ^Due = 340 t_S

Cancellare uno dei tempi e sostituire:

4,9 t_m ^Due= 340. (2,5 - t_m)

Sviluppando il termine a destra e recependo i termini, si ottiene:

4,9 t_m ^Due+340 t_m - 850 = 0

Questa è un'equazione quadratica con due soluzioni: 2.416 e -71.8. Si sceglie la soluzione positiva, che è quella che ha senso, poiché il tempo non può essere negativo e comunque deve essere inferiore a 2,5 secondi. Per questo tempo si ottiene sostituendo la profondità del pozzo:

4,9 t_m ^Due= 4,9 x 2,416^Due m = 28,6 m

-Esercizio risolto 2

Un'auto che viaggia a 90 km / h si sta avvicinando a una traversa con un semaforo. Quando sono a 70 m da lì, si accende la luce gialla, che dura 4 secondi. La distanza tra il semaforo e l'angolo successivo è di 50 m.

Il conducente ha queste due opzioni: a) frenare a - 4 m / s^Due oppure b) accelerare fino a + 2 m / s^Due. Quale delle due opzioni consente al conducente di fermarsi o attraversare l'intero viale prima che il semaforo diventi rosso?

Soluzione

La posizione di partenza del pilota è x = 0 proprio quando vede la luce gialla accendersi. È importante convertire correttamente le unità: 90 km / h equivalgono a 25 m / s.

Secondo l'opzione a), nei 4 secondi in cui dura la luce gialla, il conducente viaggia:

x (t) = v_o t + ½at^Due= 25,4 -½. (- 4) .4^Duem = 68 m (Si ferma 2 metri prima del semaforo)

Analizzando l'opzione b) abbiamo:

x (t) = v_o t + ½at^Due= 25.t + ½.2.t^Due

Finché la luce gialla dura, il conducente viaggia in questo modo:

x = 25,4 + ½,2,4^Duem = 116 m

Ma 116 m è inferiore alla distanza disponibile per arrivare alla curva successiva, che è 70 + 50 m = 120 m, quindi non può attraversare l'intera strada prima che si accenda il semaforo rosso. L'azione consigliata è frenare e rimanere a 2 metri dal semaforo.

Applicazioni

Le persone sperimentano quotidianamente gli effetti dell'accelerazione: quando si viaggia in auto o in autobus, poiché questi hanno continuamente bisogno di frenare e accelerare per adattare la velocità agli ostacoli sulla strada. L'accelerazione si verifica anche quando si sale o si scende in un ascensore.

I parchi di divertimento sono luoghi in cui le persone pagano per sperimentare gli effetti dell'accelerazione e divertirsi.

In natura, un movimento rettilineo uniformemente variato si osserva quando un oggetto viene lasciato cadere liberamente, o quando viene lanciato verticalmente verso l'alto e si aspetta che ritorni a terra. Se si trascura la resistenza dell'aria, il valore dell'accelerazione è quello della gravità: 9,8 m / s2.

Riferimenti

1. Bauer, W. 2011. Fisica per l'ingegneria e le scienze. Volume 1. Mc Graw Hill. 40-45.
2. Figueroa, D. Physics Series for Sciences and Engineering. Volume 3 °. Edizione. Cinematica. 69-85.
3. Giancoli, D. Physics: Principles with Applications. 6^th. Ed Prentice Hall. 19-36.
4. Hewitt, Paul. 2012. Scienze fisiche concettuali. 5^th. Ed. Pearson. 14-18.
5. Kirkpatrick, L. 2007. Fisica: uno sguardo al mondo. 6^ta Edizione abbreviata. Cengage Learning. 15-19.
6. Wilson, J. 2011. Fisica 10. Pearson Education. 116-119