
Caratteristiche, tipi ed esempi del moto rettilineo
Il movimento rettilineo è quello in cui il mobile si muove lungo una linea retta e quindi scorre in una dimensione, da qui viene anche chiamato moto unidimensionale. Questa linea retta è il file traiettoria o percorso seguito dall'oggetto in movimento. Le auto che si muovono lungo il viale in figura 1 seguono questo tipo di movimento.
È il modello di movimento più semplice che tu possa immaginare. I movimenti quotidiani di persone, animali e cose di solito combinano movimenti in linea retta con movimenti lungo le curve, ma alcuni che sono esclusivamente rettilinei sono frequentemente osservati.

Ecco alcuni buoni esempi:
- Quando si corre lungo un binario rettilineo di 200 metri.
- Guidare un'auto su una strada diritta.
- Far cadere liberamente un oggetto da una certa altezza.
- Quando una palla viene lanciata verticalmente verso l'alto.

Ora, l'obiettivo di descrivere un movimento viene raggiunto specificando caratteristiche come:
- Posizione
- Dislocamento
- Velocità
- Accelerazione
- Tempo metereologico.
Affinché un osservatore possa rilevare il movimento di un oggetto, deve avere un punto di riferimento (l'origine O) e aver stabilito una direzione specifica in cui muoversi, che può essere l'asse X, l'asse Y o qualsiasi altro.
Per quanto riguarda l'oggetto che si muove, può avere un numero infinito di forme. Non ci sono limitazioni al riguardo, tuttavia in tutto ciò che segue si supporrà che il mobile sia una particella; un oggetto così piccolo che le sue dimensioni non sono rilevanti.
Questo è noto per non essere il caso degli oggetti macroscopici; tuttavia, è un modello con buoni risultati nella descrizione del movimento globale di un oggetto. In questo modo, una particella può essere un'auto, un pianeta, una persona o qualsiasi altro oggetto che si muove.
Inizieremo il nostro studio della cinematica rettilinea con un approccio generale al moto e poi verranno studiati casi particolari come quelli già citati..
Indice articolo
- 1 Caratteristiche generali del moto rettilineo
- 1.1 Posizione
- 1.2 Cilindrata
- 1.3 Distanza percorsa
- 1.4 Velocità media
- 1.5 Velocità istantanea
- 1.6 Velocità
- 1.7 Accelerazione media e accelerazione istantanea
- 2 tipi
- 2.1 Moto con accelerazione costante
- 2.2 Movimenti orizzontali e movimenti verticali
- 3 esempi lavorati
- 3.1 Esempio 1
- 3.2 Esempio 2
- 4 Riferimenti
Caratteristiche generali del moto rettilineo
La seguente descrizione è generale e applicabile a qualsiasi tipo di movimento unidimensionale. La prima cosa è scegliere un sistema di riferimento. La linea lungo la quale avviene il movimento sarà l'asse X. Parametri di movimento:
Posizione

È il vettore che va dall'origine al punto in cui si trova l'oggetto in un dato istante. Nella Figura 2, il vettore X1 indica la posizione del cellulare quando è nelle coordinate P1 e lui in tempo t1. Le unità del vettore di posizione nel sistema internazionale sono metri.
Dislocamento
Lo spostamento è il vettore che indica il cambio di posizione. Nella figura 3 l'auto si è spostata dalla posizione P1 in posizione PDue, quindi il suo spostamento è ΔX = XDue - X1. Lo spostamento è la sottrazione di due vettori, è simboleggiato dalla lettera greca Δ (“delta”) ed è a sua volta un vettore. Le sue unità nel Sistema Internazionale sono metri.
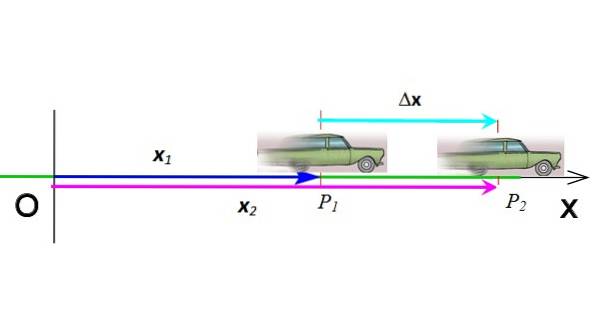
I vettori sono indicati in grassetto nel testo stampato. Ma essendo sulla stessa dimensione, se vuoi puoi fare a meno della notazione vettoriale.
Distanza percorsa
Distanza d percorso dall'oggetto in movimento è il valore assoluto del vettore di spostamento:
d = ΙΔXΙ = ΔX
Essendo un valore assoluto, la distanza percorsa è sempre maggiore o uguale a 0 e le sue unità sono le stesse di posizione e spostamento. La notazione del valore assoluto può essere eseguita con le barre modulo o semplicemente rimuovendo il grassetto nel testo stampato.
Velocità media
Quanto velocemente cambia la posizione? Ci sono cellulari lenti e cellulari veloci. La chiave è sempre stata la velocità. Per analizzare questo fattore, viene analizzata la posizione X funzione del tempo t.
Velocità media vm (vedi figura 4) è la pendenza della linea secante (fucsia) rispetto alla curva X vs t e fornisce informazioni globali sul movimento del cellulare nell'intervallo di tempo considerato.
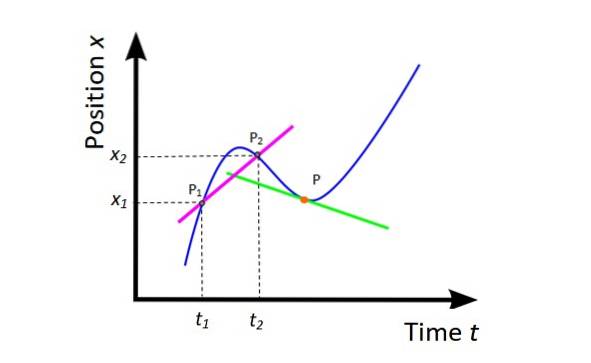
vm = (XDue - X1) / (tDue -t1) = ΔX / Δt
La velocità media è un vettore le cui unità nel sistema internazionale sono metri / secondo (SM).
Velocità istantanea
La velocità media viene calcolata prendendo un intervallo di tempo misurabile, ma non riporta ciò che accade all'interno di tale intervallo. Per conoscere la velocità in qualsiasi istante, devi rendere l'intervallo di tempo molto piccolo, matematicamente equivale a fare:
Δt → 0
L'equazione sopra è data per la velocità media. In questo modo si ottiene la velocità istantanea o semplicemente velocità:
Geometricamente, la derivata della posizione rispetto al tempo è la pendenza della retta tangente alla curva X vs t in un dato punto. Nella figura 4 il punto è arancione e la linea tangente è verde. La velocità istantanea in quel punto è la pendenza di quella linea.
Velocità
La velocità è definita come valore assoluto o modulo di velocità ed è sempre positiva (segnali, strade e autostrade sono sempre positivi, mai negativi). I termini "velocità" e "velocità" possono essere usati in modo intercambiabile su base giornaliera, ma in fisica è necessaria la distinzione tra vettore e scalare.
v = ΙvΙ = v
Accelerazione media e accelerazione istantanea
La velocità può cambiare nel corso del movimento e la realtà è che ci si aspetta che lo faccia. C'è una grandezza che quantifica questo cambiamento: l'accelerazione. Se notiamo che la velocità è il cambiamento di posizione rispetto al tempo, l'accelerazione è il cambiamento di velocità rispetto al tempo.
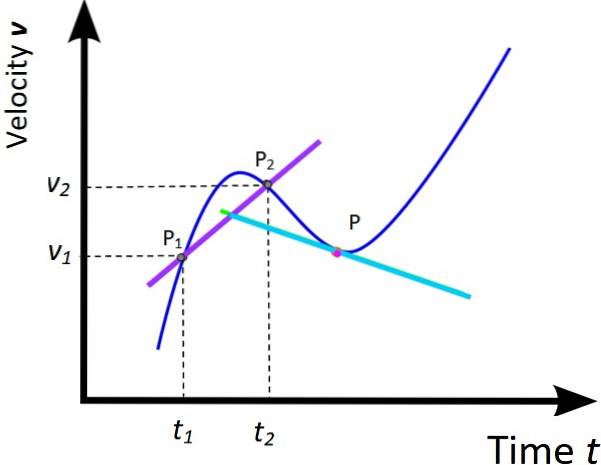
Il trattamento dato al grafico di X vs t delle due sezioni precedenti può essere esteso al corrispondente grafico di v vs t. Di conseguenza, un'accelerazione media e un'accelerazione istantanea sono definite come:
perm = (vDue - v1) / (tDue -t1) = Δv / Δt (Pendenza della linea viola)
Nel movimento unidimensionale, i vettori per convenzione hanno segni positivi o negativi a seconda che vadano in un senso o nell'altro. Quando l'accelerazione ha la stessa direzione della velocità, aumenta la sua grandezza, ma quando ha la direzione opposta e la velocità diminuisce la sua grandezza. Si dice quindi che il movimento è ritardato.
Tipi
La classificazione dei movimenti rettilinei, in generale, si basa su:
- Se l'accelerazione è costante o meno.
- Il movimento corre lungo una linea orizzontale o verticale.
Moto con accelerazione costante
Quando l'accelerazione è costante, l'accelerazione media perm è uguale all'accelerazione istantanea per e ci sono due opzioni:
- Che l'accelerazione è uguale a 0, nel qual caso la velocità è costante e c'è un moto rettilineo uniforme o MRU.
- Accelerazione costante diversa da 0, in cui la velocità aumenta o diminuisce linearmente con il tempo (il moto rettilineo uniformemente variato o MRUV):
Dove vF Y tF sono rispettivamente la velocità e il tempo finali, e vo Y to sono velocità e tempo iniziali. sì to = 0, Risolvendo per la velocità finale abbiamo l'equazione già familiare per la velocità finale:
vF = vo + a
Le seguenti equazioni sono valide anche per questo movimento:
- Posizione in funzione del tempo: x = xo + vo .t + ½ aDue
- Velocità in funzione della posizione: vFDue = voDue + 2nd.ΔX (Con Δx = x - xo)
Movimenti orizzontali e movimenti verticali
I movimenti orizzontali sono quelli che avvengono lungo l'asse orizzontale o l'asse x, mentre i movimenti verticali lo fanno lungo l'asse y. I movimenti verticali sotto l'azione della gravità sono i più frequenti e interessanti.
Nelle equazioni precedenti, prendiamo a = g = 9,8 m / sDue diretto verticalmente verso il basso, direzione che viene quasi sempre scelta con segno negativo.
In questo modo, vF = vo + a Si trasforma in vF = vo - gt e se la velocità iniziale è 0 perché l'oggetto è stato lasciato cadere liberamente, si semplifica ulteriormente a vF = - gt. Fintanto che la resistenza dell'aria non viene presa in considerazione, ovviamente.
Esempi lavorati
Esempio 1
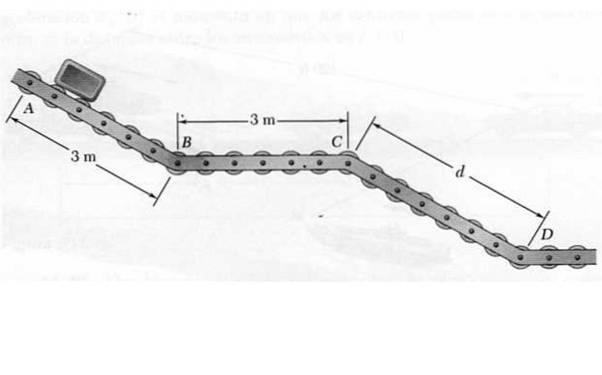
Nel punto A viene rilasciato un piccolo pacco che si muove lungo il trasportatore con ruote di scorrimento ABCD mostrato in figura. Durante la discesa delle piste AB e CD, il pacco ha un'accelerazione costante di 4,8 m / sDue, mentre nel tratto orizzontale BC mantiene la velocità costante.

Sapendo che la velocità con cui il pacchetto arriva a D è di 7,2 m / s, determinare:
a) La distanza tra C e D.
b) Il tempo necessario affinché il pacco raggiunga la fine.
Soluzione
La movimentazione del pacco viene effettuata nei tre tratti rettilinei rappresentati e per calcolare quanto richiesto è richiesta la velocità nei punti B, C e D. Analizziamo separatamente ogni tratto:
Sezione AB
Poiché l'ora non è disponibile in questa sezione, verrà utilizzata vFDue = voDue + 2nd.ΔX con vo = 0:
vFDue = 2a.Δx → vFDue= 2. 4,8 m / sDue . 3 m = 28,8 mDue/ SDue → vF = 5,37 m / s = vB
Il tempo impiegato dal pacchetto per percorrere la sezione AB è:
tAB = (vF - vo) / a = 5,37 m / s / 4,8 m / sDue = 1,19 s
Sezione BC
La velocità nella sezione BC è quindi costante vB = vC = 5,37 m / s. Il tempo impiegato dal pacchetto per viaggiare in questa sezione è:
tAVANTI CRISTO = distanza AVANTI CRISTO / vB = 3 m / 5,37 m / s = 0,56 s
Sezione CD
La velocità iniziale di questa sezione è vC = 5,37 m / s, la velocità finale è vD = 7,2 m / s, di vDDue = vCDue + 2. a. d il valore di viene cancellato d:
d = (vDDue - vCDue) /2.a = (7.2Due - 5.37Due)/Due X 4,8 m = 2,4 m
Il tempo è calcolato come:
tCD = (vD - vC) / a = (7,2 - 5,37) / 4,8 s = 0,38 s.
Le risposte alle domande poste sono:
a) d = 2,4 m
b) Il tempo di viaggio è tAB + tAVANTI CRISTO + tCD = 1,19 s +0,56 s +0,38 s = 2,13 s.
Esempio 2
Una persona si trova sotto un cancello orizzontale inizialmente aperto e alto 12 m. La persona lancia verticalmente un oggetto verso il cancello con una velocità di 15 m / s.
È noto che il cancello si chiude 1,5 secondi dopo che la persona ha lanciato l'oggetto da un'altezza di 2 metri. La resistenza dell'aria non verrà presa in considerazione. Rispondi alle seguenti domande, giustificando:
a) L'oggetto può passare attraverso il cancello prima che si chiuda?
b) L'oggetto entrerà mai in collisione con il cancello chiuso? Se sì, quando lo fa?
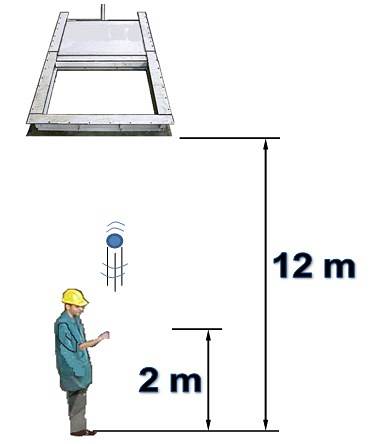
Rispondi a)
Ci sono 10 metri tra la posizione iniziale della palla e il cancello. È un lancio verticale verso l'alto, in cui questa direzione è considerata positiva.
Puoi conoscere la velocità che ci vuole per raggiungere questa quota, con questo risultato viene calcolato il tempo necessario per farlo e confrontato con il tempo di chiusura del cancello, che è di 1,5 secondi:
vF Due= vo Due- 2 g. Δe → vF = (15Due - Due X 9.8 X10)1/2 m = 5,39 m / s
t = (vF - vo) / g = (5,39 - 15) / (-9,8) s = 0,98 s
Poiché questo tempo è inferiore a 1,5 secondi, si conclude che l'oggetto può passare attraverso il cancello almeno una volta.
Risposta b)
Sappiamo già che l'oggetto riesce a passare attraverso il cancello salendo, vediamo se gli dà la possibilità di passare di nuovo in discesa. La velocità, quando si raggiunge l'altezza del cancello, ha la stessa grandezza di quando si va in salita, ma in senso inverso. Pertanto, lavoriamo con -5,39 m / se il tempo necessario per raggiungere questa situazione è:
t = (vF - vo) / g = (-5,39 - 15) / (-9,8) s = 2,08 s
Poiché il cancello rimane aperto solo per 1,5 s, è evidente che non ha tempo di ripassare prima che si chiuda, poiché lo trova chiuso. La risposta è: l'oggetto se entra in collisione con il portello chiuso dopo 2,08 secondi dopo essere stato lanciato, quando è già in discesa.
Riferimenti
- Figueroa, D. (2005). Serie: Fisica per la scienza e l'ingegneria. Volume 1. Cinematica. A cura di Douglas Figueroa (USB) .69-116.
- Giancoli, D. Physics. (2006). Principi con applicazioni. 6th Edizione. Prentice Hall. 22-25.
- Kirkpatrick, L. 2007. Fisica: uno sguardo al mondo. 6ta Edizione abbreviata. Cengage Learning. 23 - 27.
- Resnick, R. (1999). Fisico. Volume 1. Terza edizione in spagnolo. Messico. Azienda editoriale Continental S.A. de C.V. 21-22.
- Rex, A. (2011). Fondamenti di fisica. Pearson. 33 - 36
- Sears, Zemansky. 2016. Fisica universitaria con fisica moderna. 14th. Ed. Volume 1. 50 - 53.
- Serway, R., Jewett, J. (2008). Fisica per la scienza e l'ingegneria. Volume 1. 7ma. Edizione. Messico. Cengage Learning Editors. 23-25.
- Serway, R., Vulle, C. (2011). Fondamenti di fisica. 9n / A Ed. Cengage Learning. 43 - 55.
- Wilson, J. (2011). Fisica 10. Pearson Education. 133 - 149.


Nessun utente ha ancora commentato questo articolo.