
Caratteristiche e postulati del modello atomico di Dirac Jordan

Il Modello atomico Dirac-Jordan è la generalizzazione relativistica dell'operatore hamiltoniano nell'equazione che descrive la funzione d'onda quantistica dell'elettrone. A differenza del modello precedente, quello di Schrodinger, non è necessario imporre lo spin tramite il principio di esclusione di Pauli, poiché appare naturalmente.
Inoltre, il modello di Dirac-Jordan incorpora correzioni relativistiche, l'interazione spin-orbita e il termine Darwin, che spiegano la struttura fine dei livelli elettronici dell'atomo..

A partire dal 1928, gli scienziati Paul A. M. Dirac (1902-1984) e Pascual Jordan (1902-1980), decisero di generalizzare la meccanica quantistica sviluppata da Schrodinger, per includere le correzioni di Einstein della relatività speciale.
Dirac parte dall'equazione di Schrödinger, che consiste in un operatore differenziale, detto hamiltoniano, che opera su una funzione nota come la funzione d'onda dell'elettrone. Tuttavia, Schrodinger non ha tenuto conto degli effetti relativistici.
Le soluzioni della funzione d'onda ci permettono di calcolare le regioni in cui con un certo grado di probabilità l'elettrone si troverà attorno al nucleo. Queste regioni o zone vengono chiamate orbitali e dipendono da certi numeri quantici discreti, che definiscono l'energia e il momento angolare dell'elettrone.
Indice articolo
- 1 Postulati
- 1.1 I quattro postulati di Dirac
- 2 L'equazione di Dirac
- 2.1 L'atomo di Dirac-Jordan
- 2.2 Correzioni relativistiche allo spettro energetico
- 3 Articoli di interesse
- 4 Riferimenti
Postulati
Nelle teorie della meccanica quantistica, relativistiche o meno, non esiste il concetto di orbite, poiché né la posizione né la velocità dell'elettrone possono essere specificate simultaneamente. Inoltre, specificare una delle variabili porta alla totale imprecisione nell'altra..
Da parte sua, l'Hamiltoniano è un operatore matematico che agisce sulla funzione d'onda quantistica ed è costruito dall'energia dell'elettrone. Ad esempio, un elettrone libero ha un'energia totale E che dipende dal suo momento lineare p così:
E = (pDue) / 2m
Per costruire l'hamiltoniano, partiamo da questa espressione e sostituiamo p dall'operatore quantistico per quantità di moto:
p = -i ħ ∂ / ∂r
È importante notare che i termini p Y p sono diversi, poiché il primo è lo slancio e l'altro è il operatore differenziale associato allo slancio.
Inoltre, i è l'unità immaginaria e ħ la costante di Planck divisa per 2π, in questo modo si ottiene l'operatore hamiltoniano H dell'elettrone libero:
H = (ħDue/ 2 m) ∂Due / ∂rDue
Per trovare l'Hamiltoniana dell'elettrone nell'atomo, aggiungi l'interazione dell'elettrone con il nucleo:
H = (ħ2 / 2m) ∂Due / ∂rDue - eΦ (r)
Nella precedente espressione -e è la carica elettrica dell'elettrone e Φ (r) è il potenziale elettrostatico prodotto dal nucleo centrale.
Ora, l'operatore H agisce sulla funzione d'onda ψ secondo l'equazione di Schrödinger, che si scrive così:
H ψ = (io ħ ∂ / ∂t) ψ
I quattro postulati di Dirac
Primo postulato: L'equazione delle onde relativistiche ha la stessa struttura dell'equazione delle onde di Schrodinger, ciò che cambia è la H:
H ψ = (io ħ ∂ / ∂t) ψ
Secondo postulato: L'operatore hamiltoniano è costruito a partire dalla relazione energia-quantità di moto di Einstein, che si scrive come segue:
E = (mDue c4 + pDue cDue)1/2
Nella relazione precedente, se la particella ha quantità di moto p = 0, allora abbiamo la famosa equazione E = mcDue che mette in relazione l'energia a riposo di qualsiasi particella di massa m alla velocità della luce c.
Terzo postulato: per ottenere l'operatore hamiltoniano si usa la stessa regola di quantizzazione usata nell'equazione di Schrodinger:
p = -i ħ ∂ / ∂r
All'inizio, non era chiaro come gestire questo operatore differenziale che agisce all'interno di una radice quadrata, quindi Dirac si è proposto di ottenere un operatore hamiltoniano lineare sull'operatore di quantità di moto e da lì è nato il suo quarto postulato.
Quarto postulato: per sbarazzarsi della radice quadrata nella formula dell'energia relativistica, Dirac ha proposto la seguente struttura per EDue:
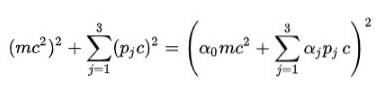
Ovviamente è necessario determinare i coefficienti alfa (α0, α1, α2, α3) perché questo sia vero.
L'equazione di Dirac
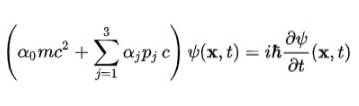
Nella sua forma compatta, l'equazione di Dirac è considerata una delle più belle equazioni matematiche del mondo:
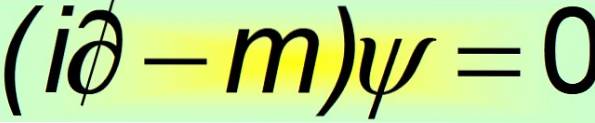
Ed è allora che diventa chiaro che le costanti alfa non possono essere quantità scalari. L'unico modo in cui viene soddisfatta l'uguaglianza del quarto postulato è che sono matrici costanti 4 × 4, note come Matrici di Dirac:
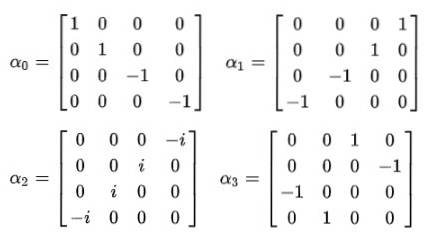
Si osserva immediatamente che la funzione d'onda cessa di essere una funzione scalare e diventa un vettore a quattro componenti chiamato spinore:
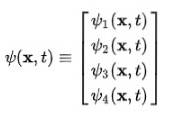
L'atomo di Dirac-Jordan
Per ottenere il modello atomico è necessario passare dall'equazione dell'elettrone libero a quella dell'elettrone nel campo elettromagnetico prodotto dal nucleo atomico. Questa interazione viene presa in considerazione incorporando il potenziale scalare Φ e il potenziale vettoriale PER nell'Hamiltoniano:
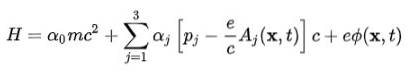
La funzione d'onda (spinore) che risulta dall'incorporazione di questa hamiltoniana ha le seguenti caratteristiche:
- Soddisfa la relatività speciale, poiché tiene conto dell'energia intrinseca dell'elettrone (primo termine dell'Hamiltoniano relativistico)
- Ha quattro soluzioni corrispondenti ai quattro componenti dello spinore
- Le prime due soluzioni corrispondono una a spin + ½ e l'altra a spin - ½
- Infine, le altre due soluzioni prevedono l'esistenza dell'antimateria, poiché corrispondono a quella dei positroni con spin opposti..
Il grande vantaggio dell'equazione di Dirac è che le correzioni all'Hamiltoniano di Schrodinger H (o) di base possono essere scomposte in diversi termini che mostreremo di seguito:
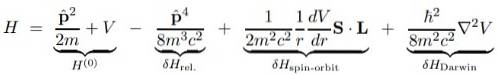
Nell'espressione precedente V è il potenziale scalare, poiché il potenziale vettore PER è nullo se si presume che il protone centrale sia stazionario e quindi non appare.
La ragione per cui le correzioni di Dirac alle soluzioni Schrödinger nella funzione d'onda sono sottili. Derivano dal fatto che gli ultimi tre termini dell'Hamiltoniano corretto sono tutti divisi per la velocità c della luce al quadrato, un numero immenso, che rende questi termini numericamente piccoli.
Correzioni relativistiche allo spettro energetico
Usando l'equazione di Dirac-Jordan troviamo correzioni allo spettro di energia dell'elettrone nell'atomo di idrogeno. Le correzioni per l'energia negli atomi con più di un elettrone in forma approssimativa si trovano anche attraverso una metodologia nota come teoria delle perturbazioni..
Allo stesso modo, il modello di Dirac consente di trovare la correzione della struttura fine nei livelli di energia dell'idrogeno..
Tuttavia, correzioni ancora più sottili come la struttura iperfine e il cambio Lamb si ottengono da modelli più avanzati come teoria quantistica dei campi, che nasce proprio dai contributi del modello Dirac.
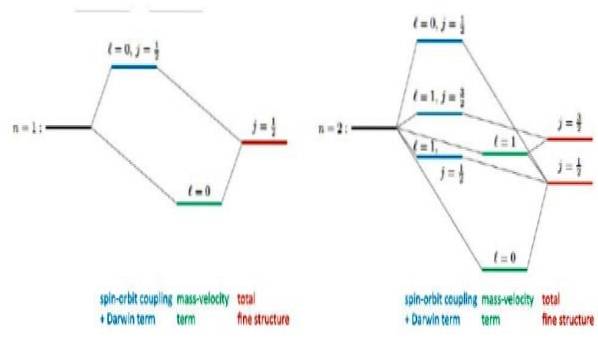
La figura seguente mostra l'aspetto delle correzioni relativistiche di Dirac ai livelli di energia:
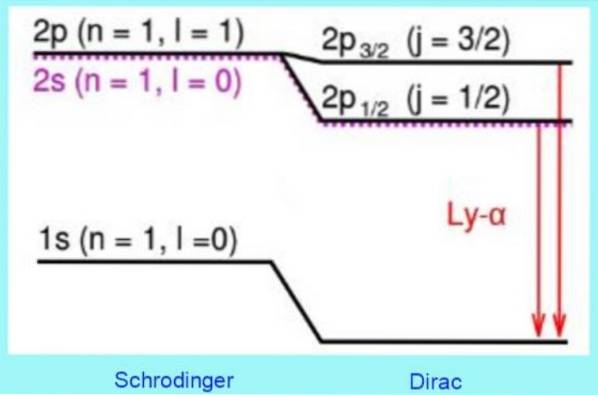
Ad esempio, le soluzioni all'equazione di Dirac prevedono correttamente uno spostamento osservato al livello 2s. È la ben nota correzione della struttura fine nella linea Lyman-alfa dello spettro dell'idrogeno (vedi figura 3).
A proposito, la struttura fine è il nome in fisica atomica per il raddoppio delle linee dello spettro di emissione degli atomi, che è una conseguenza diretta dello spin elettronico..
Articoli di interesse
Modello Atomic de Broglie.
Modello atomico di Chadwick.
Modello atomico di Heisenberg.
Il modello atomico di Perrin.
Il modello atomico di Thomson.
Modello atomico di Dalton.
Modello atomico di Schrödinger.
Modello atomico di Democrito.
Modello atomico di Leucippo.
Modello atomico di Bohr.
Modello atomico attuale.
Riferimenti
- Teoria atomica. Estratto da wikipedia.org.
- Momento magnetico dell'elettrone. Estratto da wikipedia.org.
- Quanta: un manuale di concetti. (1974). La stampa dell'università di Oxford. Recuperato da Wikipedia.org.
- Modello atomico di Dirac Jordan. Recuperato da prezi.com.
- Il nuovo universo quantistico. Cambridge University Press. Recuperato da Wikipedia.org.


Nessun utente ha ancora commentato questo articolo.