Misure di variabilità

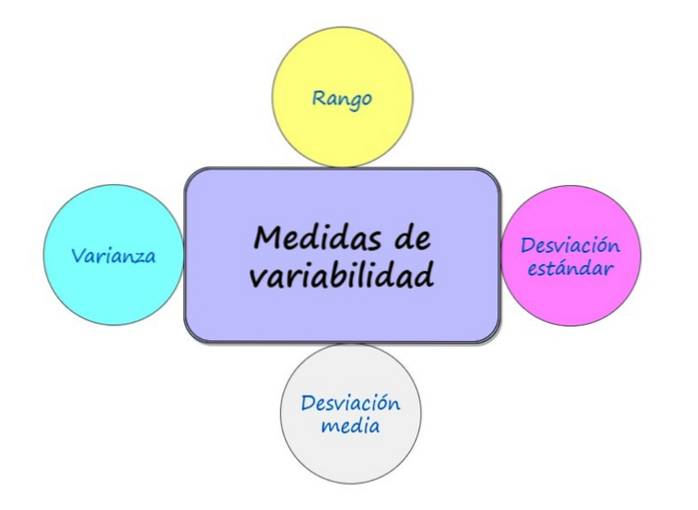
Cosa sono le misure di variabilità?

Il misure di variabilità, Chiamate anche misure di dispersione, sono indicatori statistici che indicano quanto i dati siano vicini o lontani dalla loro media aritmetica. Se i dati sono vicini alla media, la distribuzione è concentrata e se sono lontani, si tratta di una distribuzione sparsa..

Esistono molte misure di variabilità, tra le più note sono:

• Rango
• Deviazione del significato
• Varianza
• Deviazione standard

Queste misure completano le misure di tendenza centrale e sono necessarie per comprendere la distribuzione dei dati ottenuti ed estrarne quante più informazioni possibili..

Rango

L'intervallo o intervallo misura l'ampiezza di un set di dati. Per determinarne il valore, la differenza tra i dati con il valore più alto x_max e quello con il valore più basso x_min:

R = x_max - X_min

Se i dati non sono sciolti ma raggruppati per intervallo, l'intervallo viene calcolato dalla differenza tra il limite superiore dell'ultimo intervallo e il limite inferiore del primo intervallo.

Quando l'intervallo è un valore piccolo significa che tutti i dati sono abbastanza vicini tra loro, ma un intervallo ampio indica che c'è molta variabilità. È chiaro che, a parte il limite superiore e il limite inferiore dei dati, l'intervallo non tiene conto dei valori tra loro, quindi è sconsigliato utilizzarlo quando il numero di dati è elevato.

Tuttavia, è una misura immediata da calcolare e ha le stesse unità di dati, quindi è facile da interpretare.

Esempio di gamma

Di seguito l'elenco con il numero di gol segnati durante il weekend, nei campionati di calcio di nove nazioni:

40, 32, 35, 36, 37, 31, 37, 29, 39

Questo è un set di dati non raggruppato. Per trovare l'intervallo, procediamo ad ordinarli dal più basso al più alto:

29, 31, 32, 35, 36, 37, 37, 39, 40

Il dato con il valore più alto è 40 goal e quello con il valore più basso è 29 goal, quindi l'intervallo è:

R = 40−29 = 11 goal.

Si può considerare che l'intervallo è piccolo rispetto ai dati del valore minimo, che è di 29 obiettivi, quindi si può presumere che i dati non abbiano una grande variabilità.

Deviazione del significato

Questa misura di variabilità viene calcolata attraverso la media dei valori assoluti degli scostamenti rispetto alla media.. Indicare la deviazione media come D_M, Per i dati non raggruppati, la deviazione media viene calcolata utilizzando la seguente formula:

Dove n è il numero di dati disponibili, x_io rappresenta ogni dato e x̄ è la media, che è determinata sommando tutti i dati e dividendo per n:

La deviazione media permette di sapere, mediamente, in quante unità il dato si discosta dalla media aritmetica e ha il vantaggio di avere le stesse unità dei dati con cui stiamo lavorando.

Esempio di deviazione media

In base ai dati dell'esempio di intervallo, il numero di gol segnati è:

40, 32, 35, 36, 37, 31, 37, 29, 39

Se vuoi trovare la deviazione media D_M Da questi dati, è necessario prima calcolare la media aritmetica x̄:

E ora che il valore di x̄ è noto, procediamo a trovare la deviazione media D_M:

= 2,99 ≈ 3 gol

Pertanto, si può affermare che, in media, il dato è di circa 3 goal di distanza dalla media, che è di 35 goal, e come notato, è una misura molto più precisa rispetto all'intervallo..

Varianza

La deviazione media è una misura di variabilità molto più fine rispetto all'intervallo, ma poiché è calcolata attraverso il valore assoluto delle differenze tra ogni dato e la media, non offre una maggiore versatilità da un punto di vista algebrico..

Per questo motivo si preferisce la varianza, che corrisponde alla media della differenza quadratica di ogni dato con la media ed è calcolata utilizzando la formula:

In questa espressione, s^Due denota la varianza e come sempre x_io rappresenta ciascuno dei dati, x̄ è la media en è il totale dei dati.

Quando si lavora con un campione anziché con la popolazione, è preferibile calcolare la varianza in questo modo:

In ogni caso, la varianza si caratterizza per essere sempre una quantità positiva, ma poiché è la media delle differenze quadratiche, è importante notare che non ha le stesse unità di quelle dei dati..

Esempio di varianza

Per calcolare la varianza dei dati negli esempi di intervallo e deviazione media, si procede a sostituire i valori corrispondenti ed eseguire la somma indicata. In questo caso, scegliamo di dividere per n-1:

= 13,86

Deviazione standard

La varianza non ha la stessa unità di quella della variabile in esame, ad esempio, se i dati sono in metri, la varianza risulta in metri quadrati. O nell'esempio degli obiettivi sarebbe in gol al quadrato, il che non ha senso.

Pertanto, viene definita la deviazione standard, chiamata anche deviazione tipica, come radice quadrata della varianza:

s = √s^Due

In questo modo, si ottiene una misura della variabilità dei dati nelle stesse unità di questi, e più basso è il valore di s, più i dati sono raggruppati attorno alla media..

Sia la varianza che la deviazione standard sono le misure di variabilità da scegliere quando la media aritmetica è la misura della tendenza centrale che meglio descrive il comportamento dei dati..

Ed è che la deviazione standard ha una proprietà importante, nota come teorema di Chebyshev: almeno il 75% delle osservazioni si trova nell'intervallo definito da X ± 2 s. In altre parole, il 75% dei dati si trova al massimo a 2 secondi dalla media..

Allo stesso modo, almeno l'89% dei valori si trova a una distanza di 3s dalla media, percentuale che può essere ampliata, purché siano disponibili molti dati e seguano una distribuzione normale..

Figura 2.- Se i dati seguono una distribuzione normale, 95,4 di loro sono entro due deviazioni standard su entrambi i lati della media. Fonte: Wikimedia Commons.

Esempio di deviazione standard

La deviazione standard dei dati presentati negli esempi precedenti è:

s = √s^Due = √13,86 = 3,7 ≈ 4 gol