
Proprietà della matrice ortogonale, dimostrazione, esempi

Ha un matrice ortogonale quando detta matrice moltiplicata per la sua trasposizione risulta nella matrice identità. Se l'inverso di una matrice è uguale alla trasposizione, la matrice originale è ortogonale.
Le matrici ortogonali hanno la caratteristica che il numero di righe è uguale al numero di colonne. Inoltre, i vettori di riga sono vettori ortogonali unitari e anche i vettori di riga di trasposizione lo sono.
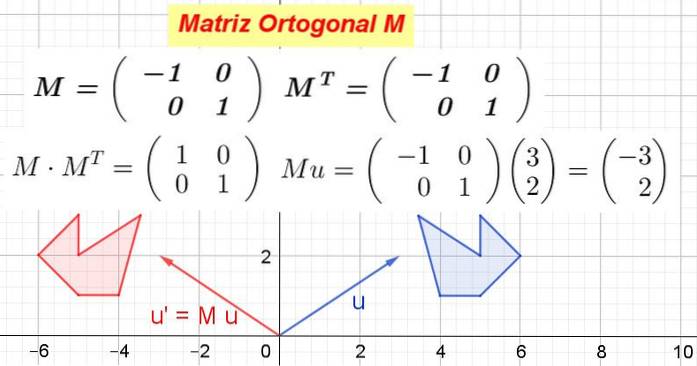
Quando una matrice ortogonale viene moltiplicata per i vettori di uno spazio vettoriale, produce a trasformazione isometrica, cioè una trasformazione che non cambia le distanze e preserva gli angoli.
Un tipico rappresentante delle matrici ortogonali sono i file matrici di rotazione. Vengono chiamate le trasformazioni di matrici ortogonali su uno spazio vettoriale trasformazioni ortogonali.
Le trasformazioni geometriche di rotazione e riflessione dei punti rappresentati dai loro vettori cartesiani vengono effettuate applicando matrici ortogonali sui vettori originali per ottenere le coordinate dei vettori trasformati. È per questo motivo che le matrici ortogonali sono ampiamente utilizzate nell'elaborazione grafica computazionale..
Indice articolo
- 1 Proprietà
- 2 Demo
- 3 esempi
- 3.1 Esempio 1
- 3.2 Esempio 2
- 3.3 Esempio 3
- 3.4 Esempio 4
- 4 Riferimenti
Proprietà
Un array M è ortogonale se moltiplicato per la sua trasposizione MT restituisce la matrice identità io. Allo stesso modo, il prodotto della trasposizione di una matrice ortogonale dalla matrice originale risulta nella matrice identità:
M MT = MT M = I
Come conseguenza dell'affermazione precedente, abbiamo che la trasposizione di una matrice ortogonale è uguale alla sua matrice inversa:
MT = M-1.
L'insieme delle matrici ortogonali dimensionali n x n formano il gruppo di ortogonali Sopra). E il sottoinsieme di Sopra) di matrici ortogonali con determinante +1 formano il Gruppo di matrici speciali unitarie SU (n). Le matrici dei gruppi SU (n) sono matrici che producono trasformazioni lineari di rotazione, note anche come gruppo rotazioni.
Dimostrazione
Mostriamo che una matrice è ortogonale se, e solo se, i vettori riga (o i vettori colonna) sono ortogonali tra loro e di norma 1.
Supponiamo che le righe di una matrice ortogonale n x n siano n vettori ortonormali di dimensione n. Se indicato da v1, vDue,…., Vn gli n vettori sono soddisfatti:
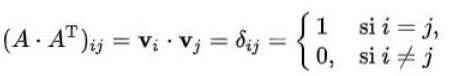
Dove è evidente che effettivamente l'insieme dei vettori riga è un insieme di vettori ortogonali di norma uno.
Esempi
Esempio 1
Mostra che la matrice 2 x 2 che nella prima riga ha il vettore v1= (-1 0) e nella sua seconda riga il vettore v2= (0 1) è una matrice ortogonale.
Soluzione: La matrice è costruita M e viene calcolata la sua trasposizione MT:
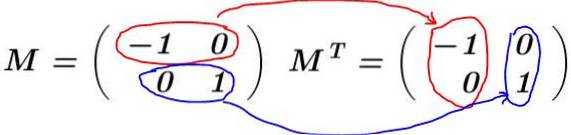
In questo esempio, l'array M è auto-trasposto, cioè la matrice e la sua trasposizione sono identiche. Si moltiplica M dalla sua trasposizione MT:
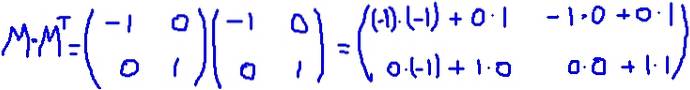
È verificato che M MT è uguale alla matrice identità:
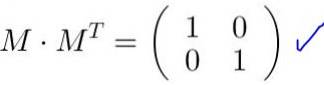
Quando la matrice M viene moltiplicato per le coordinate di un vettore o di un punto, si ottengono nuove coordinate che corrispondono alla trasformazione che la matrice fa sul vettore o punto.
La figura 1 mostra come M trasformare il vettore o sopra o' e anche come M trasforma il poligono blu nel poligono rosso. Che cosa M è ortogonale è quindi una trasformazione ortogonale, che preserva le distanze e gli angoli.
Esempio 2
Supponiamo di avere una matrice 2 x 2 definita nei reali dati dalla seguente espressione:
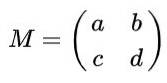
Trova i valori reali di per, b, c Y d tale che la matrice M essere una matrice ortogonale.
Soluzione: Per definizione, una matrice è ortogonale se moltiplicata per la sua trasposizione si ottiene la matrice identità. Ricordando che la matrice trasposta si ottiene dall'originale, scambiando righe per colonne, si ottiene la seguente uguaglianza:
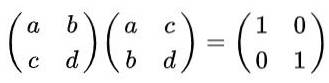
Eseguendo la moltiplicazione matriciale abbiamo:
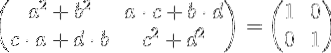
Uguagliando gli elementi della matrice sinistra con gli elementi della matrice identità a destra, otteniamo un sistema di quattro equazioni con quattro incognite a, b, ce d.
Proponiamo le seguenti espressioni per a, b, ced in termini di rapporti trigonometrici seno e coseno:
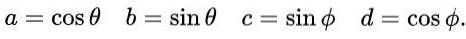
Con questa proposta e per l'identità trigonometrica fondamentale, la prima e la terza equazione sono automaticamente soddisfatte nell'uguaglianza degli elementi della matrice. La terza e la quarta equazione sono le stesse e nell'uguaglianza di matrice dopo aver sostituito i valori proposti appare così:
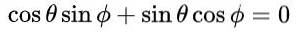
che porta alla seguente soluzione:
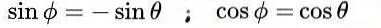
Infine, per la matrice ortogonale M si ottengono le seguenti soluzioni:
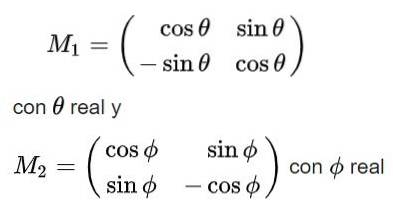
Si noti che la prima delle soluzioni ha determinante +1 quindi appartiene al gruppo SU (2), mentre la seconda soluzione ha determinante -1 e quindi non appartiene a questo gruppo.
Esempio 3
Data la matrice seguente, trova i valori di aeb in modo da avere una matrice ortogonale.
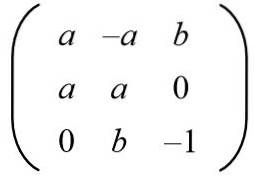
Soluzione: Affinché una data matrice sia ortogonale, il prodotto con la sua trasposizione deve essere la matrice identità. Quindi, viene eseguito il prodotto di matrice della matrice data con la sua matrice trasposta, dando il seguente risultato:
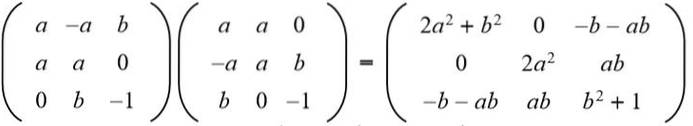
Successivamente, il risultato è equiparato alla matrice identità 3 x 3:
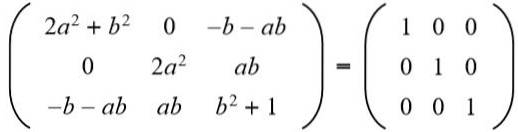
Nella seconda riga terza colonna abbiamo (a b = 0), ma per non può essere zero, perché in tal caso l'uguaglianza degli elementi della seconda riga e della seconda colonna non sarebbe soddisfatta. Quindi necessariamente b = 0. Sostituzione b per il valore 0 abbiamo:
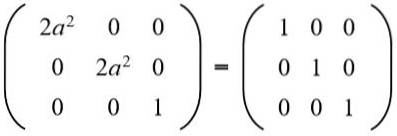
Quindi l'equazione è risolta: 2a ^ 2 = 1, le cui soluzioni sono: + ½√2 e -½√2.
Prendendo la soluzione positiva per per si ottiene la seguente matrice ortogonale:
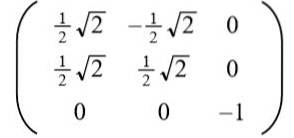
Il lettore può facilmente verificare che i vettori riga (e anche i vettori colonna) sono ortogonali e unitari, cioè ortonormali.
Esempio 4
Dimostralo la matrice PER i cui vettori riga sono v1 = (0, -1 0), v2 = (1, 0, 0) Y v3 = (0 0-1) è una matrice ortogonale. Inoltre scopri come vengono trasformati i vettori della base canonica I J K ai vettori u1, u2 Y u3.
Soluzione: Va ricordato che l'elemento (i, j) di una matrice moltiplicato per la sua trasposizione, è il prodotto scalare del vettore della riga (i) per quello della colonna (j) della trasposizione. Inoltre, questo prodotto è uguale al delta di Kronecker nel caso in cui la matrice sia ortogonale:
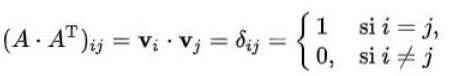
Nel nostro caso assomiglia a questo:
v1 • v1 = 0x0 + (-1) x (-1) + 0x0 = 1
v2 • v2 = 1 × 1 + 0x0 + 0x0 = 1
v3 • v3 = 0x0 + 0x0 + (-1) x (-1) = 1
v1 • v2 = 0x1 + (-1) x0 + 0x0 = 0
v2 • v1 = 1 × 0 + 0x (-1) + 0x0 = 0
v2 • v3 = 1 × 0 + 0x (0) + 0x (-1) = 0
v3 • v2 = 0x1 + 0x (0) + (-1) x0 = 0
v1 • v3 = 0x0 + (-1) x (0) + 0x (-1) = 0
v3 • v1 = 0x0 + 0x (-1) + (-1) x0 = 0
Con il quale si dimostra che si tratta di una matrice ortogonale.
Cosa c'è di più u1 = A i = (0, 1, 0); u2 = A j = (-1, 0, 0) e infine u3 = A k = (0, 0, -1)
Riferimenti
- Anthony Nicolaides (1994) Determinants & Matrices. Passa la pubblicazione.
- Birkhoff e MacLane. (1980). Algebra moderna, ed. Vicens-Vives, Madrid.
- Casteleiro Villalba M. (2004) Introduzione all'algebra lineare. Editoriale ESIC.
- Dave Kirkby (2004) Maths Connect. Heinemann.
- Jenny Olive (1998) Maths: A Student's Survival Guide. Cambridge University Press.
- Richard J. Brown (2012) 30-Second Maths: The 50 Most-Expanding Theories in Mathematics. Ivy press limited.
- Wikipedia. Matrice ortogonale. Estratto da: es.wikipedia.com
- Wikipedia. Matrice ortogonale. Estratto da: en.wikipedia.com



Nessun utente ha ancora commentato questo articolo.