
Storia, ipotesi ed esercizi della legge di Hardy-Weinberg
Il legge di Hardy-Weinberg, Chiamato anche principio di Hardy-Weinberg o equilibrio, consiste in un teorema matematico che descrive un'ipotetica popolazione diploide con riproduzione sessuale che non si evolve - le frequenze alleliche non cambiano di generazione in generazione.
Questo principio presuppone cinque condizioni necessarie affinché la popolazione rimanga costante: assenza di flusso genico, assenza di mutazioni, accoppiamento casuale, assenza di selezione naturale e dimensioni della popolazione infinitamente grandi. In questo modo, in assenza di queste forze, la popolazione rimane in equilibrio.
Quando una qualsiasi delle ipotesi di cui sopra non è soddisfatta, si verifica un cambiamento. Per questo motivo, la selezione naturale, la mutazione, le migrazioni e la deriva genetica sono i quattro meccanismi evolutivi..
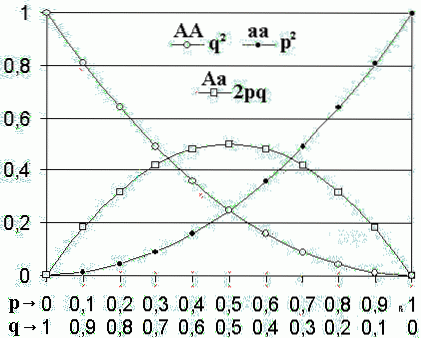
Secondo questo modello, quando le frequenze alleliche di una popolazione sono p Y che cosa, le frequenze genotipiche saranno pDue, Duepq Y che cosaDue.
Possiamo applicare l'equilibrio di Hardy-Weinberg nel calcolo delle frequenze di alcuni alleli di interesse, ad esempio, per stimare la proporzione di eterozigoti in una popolazione umana. Possiamo anche verificare se una popolazione è in equilibrio e proporre ipotesi che le forze agiscano su quella popolazione..
Indice articolo
- 1 Prospettiva storica
- 2 Genetica delle popolazioni
- 3 Qual è l'equilibrio di Hardy-Weinberg?
- 3.1 Notazione
- 4 Esempio
- 4.1 Prima generazione di topi
- 4.2 Seconda generazione di topi
- 5 Presupposti dell'equilibrio di Hardy-Weinberg
- 5.1 La popolazione è infinitamente numerosa
- 5.2 Non c'è flusso genico
- 5.3 Non ci sono mutazioni
- 5.4 Accoppiamento casuale
- 5.5 Nessuna selezione
- 6 Problemi risolti
- 6.1 Frequenza dei portatori di fenilchetonuria
- 6.2 Risposta
- 6.3 La seguente popolazione è in equilibrio di Hardy-Weinberg??
- 6.4 Popolazione di farfalle
- 7 Riferimenti
Prospettiva storica
Il principio Hardy-Weinberg è nato nel 1908 e deve il suo nome ai suoi scienziati G.H. Hardy e W. Weinberg, che sono giunti indipendentemente alle stesse conclusioni.
Prima di allora, un altro biologo di nome Udny Yule aveva affrontato il problema nel 1902. Yule iniziò con una serie di geni in cui le frequenze di entrambi gli alleli erano 0,5 e 0,5. Il biologo ha dimostrato che le frequenze sono state mantenute durante le generazioni successive.
Sebbene Yule concludesse che le frequenze alleliche potevano essere mantenute stabili, la sua interpretazione era troppo letterale. Credeva che l'unico stato di equilibrio fosse trovato quando le frequenze corrispondevano al valore di 0,5.
Yule ha discusso animatamente delle sue nuove scoperte con R.C. Punnett - ampiamente conosciuto nel campo della genetica per l'invenzione della famosa "piazza Punnett". Sebbene Punnett sapesse che Yule aveva torto, non trovò un modo matematico per dimostrarlo..
Pertanto, Punnett ha contattato il suo amico matematico Hardy, che è riuscito a risolverlo immediatamente, ripetendo i calcoli utilizzando variabili generali, e non il valore fisso di 0,5 come aveva fatto Yule..
Genetica della popolazione
La genetica delle popolazioni mira a studiare le forze che portano a cambiamenti nelle frequenze alleliche nelle popolazioni, integrando la teoria dell'evoluzione per selezione naturale di Charles Darwin e la genetica mendeliana. Oggi, i suoi principi forniscono la base teorica per comprendere molti aspetti della biologia evolutiva..
Una delle idee cruciali della genetica delle popolazioni è la relazione tra i cambiamenti nell'abbondanza relativa dei tratti e i cambiamenti nell'abbondanza relativa degli alleli che la regolano, spiegata dal principio di Hardy-Weinberg. In effetti, questo teorema fornisce la struttura concettuale per la genetica delle popolazioni..
Alla luce della genetica delle popolazioni, il concetto di evoluzione è il seguente: cambiamento delle frequenze alleliche nel corso delle generazioni. Quando non c'è cambiamento, non c'è evoluzione.
Qual è l'equilibrio di Hardy-Weinberg?
L'equilibrio di Hardy-Weinberg è un modello nullo che ci consente di specificare il comportamento delle frequenze geniche e alleliche attraverso le generazioni. In altre parole, è il modello che descrive il comportamento dei geni nelle popolazioni, in una serie di condizioni specifiche..
Notazione
Nel teorema di Hardy-Weinbergm la frequenza allelica di PER (allele dominante) è rappresentato dalla lettera p, mentre la frequenza allelica di per (allele recessivo) è rappresentato dalla lettera che cosa.
Le frequenze genotipiche attese sono pDue, Duepq Y che cosaDue, per la dominante omozigote (aa), eterozigote (Aa) e omozigote recessivo (aa), rispettivamente.
Se ci sono solo due alleli in quel locus, la somma delle frequenze dei due alleli deve necessariamente essere uguale a 1 (p + q = 1). L'espansione binomiale (p + q)Due rappresentano le frequenze genotipiche pDue + Duepq + qDue = 1.
Esempio
In una popolazione, gli individui che lo compongono si incrociano per dare origine alla prole. In generale, possiamo segnalare gli aspetti più importanti di questo ciclo riproduttivo: la produzione di gameti, la loro fusione per dare origine a uno zigote e lo sviluppo dell'embrione per dare origine alla nuova generazione..
Immagina di poter rintracciare il processo genico mendeliano negli eventi menzionati. Lo facciamo perché vogliamo sapere se e perché un allele o un genotipo aumenterà o diminuirà di frequenza..
Per capire come variano le frequenze dei geni e degli alleli in una popolazione, seguiremo la produzione di gameti di un insieme di topi. Nel nostro esempio ipotetico, l'accoppiamento avviene in modo casuale, dove tutti gli spermatozoi e le uova vengono mescolati casualmente..
Nel caso dei topi, questa ipotesi non è vera ed è solo una semplificazione per facilitare i calcoli. Tuttavia, in alcuni gruppi di animali, come alcuni echinodermi e altri organismi acquatici, i gameti vengono espulsi e si scontrano casualmente..
Prima generazione di topi
Ora, concentriamo la nostra attenzione su un locus specifico, con due alleli: PER Y per. Seguendo la legge enunciata da Gregor Mendel, ogni gamete riceve un allele dal locus A. Supponiamo che il 60% degli ovuli e dello sperma riceva l'allele PER, mentre il restante 40% ha ricevuto l'allele per.
Quindi, la frequenza dell'allele PER è 0,6 e quello dell'allele per è 0.4. Questo gruppo di gameti verrà trovato casualmente per dare origine a uno zigote, qual è la probabilità che formino ciascuno dei tre possibili genotipi? Per fare ciò, dobbiamo moltiplicare le probabilità come segue:
Genotipo aa: 0,6 x 0,6 = 0,36.
Genotipo Aa: 0,6 x 0,4 = 0,24. Nel caso dell'eterozigote, ci sono due forme in cui può originarsi. Il primo che lo sperma porta l'allele PER e l'ovulo l'allele per, o il caso inverso, lo sperma il per e l'ovulo PER. Quindi aggiungiamo 0,24 + 0,24 = 0,48.
Genotipo aa: 0,4 x 0,4 = 0,16.
Seconda generazione di topi
Ora, immaginiamo che questi zigoti si sviluppino e diventino topi adulti che produrranno nuovamente gameti, ci aspetteremmo che le frequenze alleliche siano le stesse o diverse dalla generazione precedente?
Genotipo aa produrrà il 36% dei gameti, mentre gli eterozigoti produrranno il 48% dei gameti e il genotipo aa 16%.
Per calcolare la nuova frequenza allelica, aggiungiamo la frequenza dell'omozigote più la metà dell'eterozigote, come segue:
Frequenza allelica PER: 0,36 + ½ (0,48) = 0,6.
Frequenza allelica per: 0,16 + ½ (0,48) = 0,4.
Se li confrontiamo con le frequenze iniziali, ci accorgeremo che sono identici. Pertanto, secondo il concetto di evoluzione, poiché non ci sono cambiamenti nelle frequenze alleliche nel corso delle generazioni, la popolazione è in equilibrio - non si evolve..
Ipotesi di equilibrio di Hardy-Weinberg
Quali condizioni deve soddisfare la popolazione precedente affinché le sue frequenze alleliche rimangano costanti nel corso delle generazioni? Nel modello di equilibrio di Hardy-Weinberg, la popolazione che non si evolve soddisfa i seguenti presupposti:
La popolazione è infinitamente grande
La popolazione deve essere di dimensioni estremamente grandi per evitare effetti stocastici o casuali della deriva genica.
Quando le popolazioni sono piccole, l'effetto della deriva genica (cambiamenti casuali nelle frequenze alleliche, da una generazione all'altra) a causa dell'errore di campionamento è molto maggiore e può portare alla fissazione o alla perdita di alcuni alleli..
Non c'è flusso genico
Le migrazioni non esistono nella popolazione, quindi gli alleli che possono alterare le frequenze geniche non possono arrivare o partire.
Non ci sono mutazioni
Le mutazioni sono cambiamenti nella sequenza del DNA e possono avere cause diverse. Questi cambiamenti casuali modificano il pool genetico nella popolazione, mediante l'introduzione o l'eliminazione di geni nei cromosomi.
Accoppiamento casuale
La miscelazione dei gameti deve essere eseguita in modo casuale, come l'ipotesi che abbiamo usato nell'esempio del topo. Pertanto, non dovrebbe esserci una scelta del partner tra gli individui nella popolazione, inclusa la consanguineità (riproduzione di individui che sono imparentati).
Quando l'accoppiamento non è casuale, non provoca un cambiamento nelle frequenze alleliche da una generazione all'altra, ma può generare deviazioni dalle frequenze genotipiche attese..
Nessuna selezione
Non esiste un successo riproduttivo differenziale di individui con genotipi diversi che possono alterare le frequenze alleliche all'interno della popolazione..
In altre parole, nella popolazione ipotetica tutti i genotipi hanno la stessa probabilità di riprodursi e sopravvivere..
Quando una popolazione non soddisfa queste cinque condizioni, il risultato è l'evoluzione. Logicamente, le popolazioni naturali non soddisfano questi presupposti. Pertanto, il modello di Hardy-Weinberg viene utilizzato come ipotesi nulla che ci consente di effettuare stime approssimative del gene e delle frequenze alleliche..
Oltre alla mancanza di queste cinque condizioni, ci sono altre possibili cause per cui la popolazione non è in equilibrio.
Uno di questi si verifica quando loci sono legati al sesso o a fenomeni di distorsione nella segregazione o unità meiotica (quando ogni copia di un gene o di un cromosoma non viene trasmessa con la stessa probabilità alla generazione successiva).
Problemi risolti
Frequenza di corrieri di fenilchetonuria
Negli Stati Uniti, si stima che uno su 10.000 neonati abbia una condizione chiamata fenilchetonuria..
Questo disturbo è espresso solo negli omozigoti recessivi in un disturbo metabolico. Conoscendo questi dati, qual è la frequenza dei portatori della malattia nella popolazione??
Risposta
Per applicare l'equazione di Hardy-Weinberg dobbiamo presumere che la scelta del partner non sia correlata al gene correlato alla patologia e non vi sia consanguineità.
Inoltre, assumiamo che non ci siano fenomeni migratori negli Stati Uniti, non ci siano nuove mutazioni di fenilchetonuria e la probabilità di riproduzione e sopravvivenza sia la stessa tra i genotipi..
Se le condizioni sopra menzionate sono vere, possiamo usare l'equazione di Hardy-Weinberg per eseguire calcoli rilevanti per il problema..
Sappiamo che c'è un caso di malattia ogni 10.000 nascite, quindi che cosaDue = 0,0001 e la frequenza dell'allele recessivo sarà la radice quadrata di questo valore: 0,01.
Che cosa p = 1 - che cosa, dobbiamo p è 0,99. Ora abbiamo la frequenza di entrambi gli alleli: 0,01 e 0,99. La frequenza portante si riferisce alla frequenza degli eterozigoti calcolata come 2pq. Quindi, 2pq = 2 x 0,99 x 0,01 = 0,0198.
Ciò equivale a circa il 2% della popolazione. Ricorda che questo è solo un risultato approssimativo.
La seguente popolazione è in equilibrio di Hardy-Weinberg??
Se conosciamo il numero di ciascun genotipo nella popolazione, possiamo concludere se è nell'equilibrio di Hardy-Weinberg. I passaggi per risolvere questi tipi di problemi sono i seguenti:
- Calcola le frequenze genotipiche osservate (D, H Y R)
- Calcola le frequenze alleliche (p Y che cosa)
p = D + ½ H
q = R + ½ H
- Calcola le frequenze genotipiche attese (pDue, Dueperché e cosaDue)
- Calcola i numeri attesi (pDue, Dueperché e cosaDue), moltiplicando questi valori per il numero di individui totali
- Confronta i numeri attesi con quelli osservati con il test di XDue di Pearson.
Popolazione di farfalle
Ad esempio, vogliamo verificare se la seguente popolazione di farfalle è in equilibrio di Hardy-Weinberg: ci sono 79 individui di genotipo dominante omozigote (aa), 138 dell'eterozigote (Aa) e 61 dell'omozigote recessivo (aa).
Il primo passo è calcolare le frequenze osservate. Lo facciamo dividendo il numero di individui per genotipo per il numero totale di individui:
D = 79/278 = 0,28
H = 138/278 = 0,50
R = 61/278 = 0,22
Verificare se ho fatto bene è il primo passo, aggiungo tutte le frequenze e dovrebbe dare 1.
Il secondo passo è calcolare le frequenze alleliche.
p = 0,28 + ½ (0,50) = 0,53
che cosa = 0,22 + ½ (0,50) = 0,47
Con questi dati, posso calcolare le frequenze genotipiche attese (pDue, Dueperché e cosaDue)
pDue = 0.28
Duepq = 0,50
che cosaDue = 0.22
Calcolo i numeri attesi, moltiplicando le frequenze attese per il numero di individui. In questo caso, il numero di individui osservati e attesi è identico, quindi posso concludere che la popolazione è in equilibrio.
Quando i numeri ottenuti non sono identici, devo applicare il citato test statistico (XDue di Pearson).
Riferimenti
- Andrews, C. (2010). Il principio di Hardy-Weinberg. Conoscenza dell'educazione sulla natura 3 (10): 65.
- Audesirk, T., Audesirk, G. e Byers, B. E. (2004). Biologia: scienza e natura. Pearson Education.
- Freeman, S., & Herron, J. C. (2002). Analisi evolutiva. Prentice Hall.
- Futuyma, D. J. (2005). Evoluzione . Sinauer.
- Hickman, C. P., Roberts, L. S., Larson, A., Ober, W. C., & Garrison, C. (2001). Principi integrati di zoologia (Vol.15). New York: McGraw-Hill.
- Soler, M. (2002). Evoluzione: le basi della biologia. Progetto Sud.



Nessun utente ha ancora commentato questo articolo.