Il Legge di Faraday nell'elettromagnetismo si afferma che un flusso di campo magnetico variabile è in grado di indurre una corrente elettrica in un circuito chiuso.
Nel 1831, il fisico inglese Michael Faraday sperimentò conduttori in movimento all'interno di un campo magnetico e anche campi magnetici variabili che passavano attraverso conduttori fissi..
Faraday si rese conto che se variava il flusso del campo magnetico nel tempo, era in grado di stabilire una tensione proporzionale a quella variazione. Se ε è la tensione o forza elettromotrice indotta (emf indotta) e Φ è il flusso del campo magnetico, in forma matematica può essere espresso:
| ε | = ΔΦ / Δt
Dove il simbolo Δ indica la variazione della quantità e le barre nella fem indicano il valore assoluto di questa. Poiché si tratta di un circuito chiuso, la corrente può fluire in una direzione o nell'altra.
Il flusso magnetico, prodotto da un campo magnetico su una superficie, può variare in diversi modi, ad esempio:
-Spostamento di una barra magnetica attraverso un anello circolare.
-Aumentando o diminuendo l'intensità del campo magnetico che attraversa il loop.
-Lasciando il campo fisso, ma tramite qualche meccanismo cambia l'area del loop.
-Combinando i metodi di cui sopra.
Indice articolo
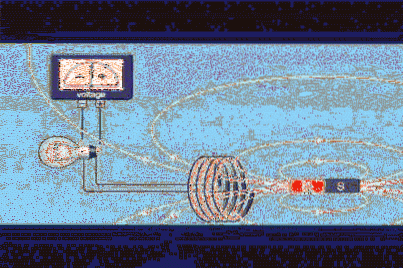
Supponiamo di avere un circuito chiuso dell'area A, come un anello circolare o un avvolgimento uguale a quello di figura 1, e di avere un magnete che produce un campo magnetico B.
Il flusso di campo magnetico Φ è una quantità scalare che si riferisce al numero di linee di campo che attraversano l'area A. Nella figura 1 ci sono le linee bianche che lasciano il polo nord del magnete e ritornano attraverso il sud.
L'intensità del campo sarà proporzionale al numero di linee per unità di area, quindi possiamo vedere che ai poli è molto intenso. Ma possiamo avere un campo molto intenso che non produce flusso nel loop, che possiamo ottenere cambiando l'orientamento di questo (o del magnete).
Per tenere conto del fattore di orientamento, il flusso del campo magnetico è definito come il prodotto scalare tra B Y n, essere n il vettore normale unitario alla superficie del loop e che indica il suo orientamento:
Φ = B•n A = BA.cosθ
Dove θ è l'angolo tra B Y n. Se per esempio B Y n sono perpendicolari, il flusso del campo magnetico è zero, perché in quel caso il campo è tangente al piano della spira e non può passare attraverso la sua superficie.
Invece sì B Y n sono paralleli, significa che il campo è perpendicolare al piano del loop e le linee lo attraversano il più lontano possibile.
L'unità nel sistema internazionale per F è il weber (W), dove 1 W = 1 T.mDue (leggi "tesla per metro quadrato").
Nella figura 1 possiamo vedere che la polarità della tensione cambia quando il magnete si muove. La polarità è stabilita dalla legge di Lenz, la quale afferma che la tensione indotta deve opporsi alla variazione che la produce.
Se, ad esempio, il flusso magnetico prodotto dal magnete aumenta, si stabilisce nel conduttore una corrente che circola creando un proprio flusso, che si oppone a tale aumento..
Se, al contrario, il flusso creato dal magnete diminuisce, la corrente indotta circola in modo tale che il proprio flusso contrasti tale diminuzione..
Per tenere conto di questo fenomeno viene posto un segno negativo prima della legge di Faraday e non è più necessario posizionare le barre del valore assoluto:
ε = -ΔΦ / Δt
Questa è la legge di Faraday-Lenz. Se la variazione di flusso è infinitesimale, i delta vengono sostituiti da differenziali:
ε = -dΦ / dt
L'equazione precedente è valida per un ciclo. Ma se abbiamo una bobina di N spire, il risultato è molto migliore, perché l'emf viene moltiplicato N volte:
ε = - N (dΦ / dt)
Affinché la corrente accenda la lampadina da produrre, deve esserci un movimento relativo tra il magnete e il circuito. Questo è uno dei modi in cui il flusso può variare, perché in questo modo cambia l'intensità del campo che passa attraverso il loop..
Non appena il movimento del magnete cessa, la lampadina si spegne, anche se il magnete rimane fermo al centro del cappio. Ciò che serve per far circolare la corrente che accende la lampadina è che il flusso di campo varia.
Quando il campo magnetico varia nel tempo, possiamo esprimerlo come:
B = B (t).
Mantenendo costante l'area A del loop e lasciandola fissa ad un angolo costante, che nel caso della figura è 0º, allora:
Se è possibile cambiare l'area del loop, lasciando fisso il suo orientamento e posizionandolo al centro di un campo costante, la fem indotta è data da:
Un modo per ottenere ciò è mettere una barra che scorre su una guida conduttrice ad una certa velocità, come mostrato nella figura seguente.
La barra e il binario, più una lampadina o una resistenza collegata con fili conduttivi, formano un circuito chiuso a forma di anello rettangolare..
Quando si fa scorrere la barra, la lunghezza X aumenta o diminuisce, e con esso cambia l'area del loop, il che è sufficiente per creare un flusso variabile.
Come abbiamo detto prima, se l'angolo tra B e la normale del loop viene fatta variare, il flusso di campo cambia in base a:
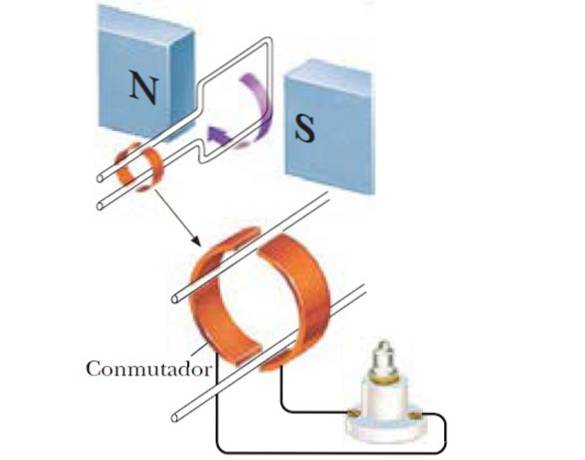
Si ottiene così un generatore sinusoidale, e se invece di una singola bobina viene utilizzato un numero N di bobine, la fem indotta è maggiore:
Una bobina circolare di N spire e raggio R, ruota con frequenza angolare ω nel mezzo di un campo magnetico di magnitudine B. Trova un'espressione per la fem massima indotta nella bobina.
L'espressione per la fem indotta dalla rotazione viene applicata quando la bobina ha N spire, sapendo che:
-L'area della bobina è A = πRDue
-L'angolo θ varia in funzione del tempo come θ = ωt
È importante notare che il primo θ = ωt è sostituito nella legge di Faraday e presto è derivato rispetto al tempo:
ε = -NBA (cos θ) '= -NB (πRDue). [cos (ωt)] '= NBω (πRDue) sin (ωt)
Poiché viene richiesta la fem massima, si verifica ogni volta che sin ωt = 1, quindi alla fine:
εmax = NBω (πRDue)
Nessun utente ha ancora commentato questo articolo.