
Caratteristiche, elementi, tipi, applicazioni delle lenti divergenti
Il lenti divergenti Sono quelli più sottili nella parte centrale e più spessi ai bordi. Di conseguenza, separano (divergono) i raggi luminosi che li colpiscono parallelamente all'asse principale. Le sue estensioni finiscono per convergere nella messa a fuoco dell'immagine situata a sinistra dell'obiettivo.
Lenti divergenti, o negative come vengono anche chiamate, formano quelle che vengono chiamate immagini virtuali di oggetti. Hanno varie applicazioni. In particolare, in oftalmologia vengono utilizzati per correggere la miopia e alcuni tipi di astigmatismo.

Quindi, se sei miope e indossi gli occhiali, hai un perfetto esempio di lente divergente a portata di mano..
Indice articolo
- 1 Caratteristiche delle lenti divergenti
- 2 Elementi dell'obiettivo divergenti
- 3 Imaging
- 4 Applicazioni
- 5 tipi
- 6 Differenze con lenti convergenti
- 7 Equazione gaussiana delle lenti e ingrandimento di una lente
- 7.1 Equazione gaussiana
- 8 Esercizio risolto
- 9 Riferimenti
Caratteristiche delle lenti divergenti
Come spiegato in precedenza, le lenti divergenti sono più strette nella loro parte centrale rispetto ai bordi. Inoltre, in questo tipo di lente una delle sue superfici è sempre concava. Ciò conferisce a questo tipo di obiettivo una serie di caratteristiche.
Per cominciare, il prolungamento dei raggi che li investono si traduce in immagini virtuali che non possono essere raccolte su nessun tipo di schermo. È così, perché i raggi che passano attraverso l'obiettivo non convergono in nessun punto, poiché divergono in tutte le direzioni. Inoltre, a seconda della curvatura della lente, i raggi si apriranno in misura maggiore o minore..
Un'altra caratteristica importante di questo tipo di obiettivo è che il fuoco è a sinistra dell'obiettivo, quindi si trova tra esso e l'oggetto..
Inoltre, nelle lenti divergenti le immagini sono più piccole dell'oggetto e si trovano tra l'oggetto e il fuoco..

Elementi dell'obiettivo divergenti
Quando si studiano, è essenziale sapere quali elementi compongono le lenti in generale e le lenti divergenti in particolare..
Il punto attraverso il quale i raggi non vengono deviati è chiamato il centro ottico di una lente. L'asse principale, da parte sua, è la linea che unisce detto punto e il fuoco principale, quest'ultimo essendo rappresentato dalla lettera F.
Il nome del fuoco principale è il punto in cui tutti i raggi che colpiscono l'obiettivo si trovano paralleli all'asse principale..
In questo modo, la distanza tra il centro ottico e il fuoco viene chiamata lunghezza focale..
I centri di curvatura sono definiti come i centri delle sfere che creano la lente; I raggi di curvatura sono quindi i raggi delle sfere che danno origine alla lente. Infine, il piano centrale dell'obiettivo è chiamato piano ottico.Imaging
Per determinare graficamente la formazione di un'immagine in una lente sottile, è sufficiente conoscere la direzione che seguiranno due dei tre raggi
di cui si conosce la traiettoria.
Uno di questi è quello che colpisce l'obiettivo parallelamente all'asse ottico dell'obiettivo. Questa, una volta rifratta nell'obiettivo, passerà attraverso la messa a fuoco dell'immagine. Il secondo dei raggi di cui si conosce il percorso è quello attraverso il centro ottico. Questo non vedrà la sua traiettoria modificata.
Il terzo e ultimo è quello che passa attraverso il fuoco dell'oggetto (o la sua estensione attraversa il fuoco dell'oggetto) che dopo la rifrazione seguirà una direzione parallela a quella dell'asse ottico della lente..
In questo modo, in generale, si formerà un tipo di immagine o un'altra nelle lenti a seconda della posizione dell'oggetto o del corpo rispetto alla lente..
Tuttavia, nel caso particolare di lenti divergenti, qualunque sia la posizione del corpo davanti alla lente, l'immagine che si andrà a formare avrà determinate caratteristiche. Ed è che in lenti divergenti l'immagine sarà sempre virtuale, più piccola del corpo e giusta.
Applicazioni
Il fatto che possano separare la luce che li attraversa conferisce alle lenti divergenti alcune qualità interessanti nel campo dell'ottica. In questo modo, possono correggere la miopia e alcuni tipi specifici di astigmatismo.
Le lenti oftalmiche divergenti separano i raggi luminosi in modo che quando raggiungono l'occhio umano siano più distanti. Pertanto, quando attraversano la cornea e il cristallino, vanno oltre e possono raggiungere la retina, causando problemi di vista nelle persone con miopia..
Tipi
Come abbiamo già discusso, le lenti convergenti hanno almeno una superficie concava. Per questo motivo, ci sono tre tipi di lenti divergenti: biconcave, piano-concave e convesse-concave..
Le lenti biconcave divergenti sono costituite da due superfici concave, le lenti piano-concave hanno una superficie concava e una piatta, mentre nel menisco convesso-concavo o divergente una superficie è leggermente convessa e l'altra è concava..
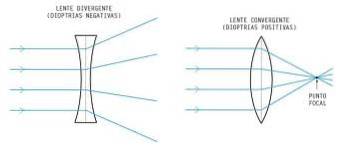
Differenze con lenti convergenti
Nelle lenti convergenti, contrariamente a quanto accade nelle lenti divergenti, lo spessore diminuisce dal centro verso i bordi. Pertanto, in questo tipo di lenti, i raggi luminosi che cadono parallelamente all'asse principale sono concentrati o convergono in un unico punto (al fuoco). In questo modo creano sempre immagini reali degli oggetti.
In ottica le lenti convergenti o positive vengono utilizzate principalmente per correggere l'ipermetropia, la presbiopia e alcuni tipi di astigmatismo.
Equazione gaussiana delle lenti e ingrandimento di una lente
Il tipo di lenti che vengono studiate più comunemente sono chiamate lenti sottili. Questo definisce tutte le lenti il cui spessore è molto piccolo rispetto ai raggi di curvatura delle superfici che le limitano..
Lo studio di questo tipo di lente può essere svolto principalmente attraverso due equazioni: l'equazione gaussiana e l'equazione che permette di determinare l'ingrandimento della lente..
Equazione di Gauss
L'importanza dell'equazione gaussiana per lenti sottili risiede nel gran numero di problemi ottici di base che consente di risolvere. La sua espressione è la seguente:
1 / f = 1 / p + 1 / q
Dove 1 / f è la potenza dell'obiettivo ef è la lunghezza focale o la distanza dal centro ottico al fuoco F. L'unità di misura della potenza di una lente è la diottria (D), il valore è 1 D = 1 m-1. D'altra parte, p e q sono, rispettivamente, la distanza alla quale si trova un oggetto e la distanza alla quale viene osservata la sua immagine.
Esercizio risolto
Un corpo è posizionato a 40 centimetri da una lente divergente di -40 centimetri di lunghezza focale. Calcola l'altezza dell'immagine se l'altezza dell'oggetto è di 5 cm. Determina anche se l'immagine è diritta o invertita.
Abbiamo i seguenti dati: h = 5 cm; p = 40 cm; f = -40 cm.
Questi valori sono sostituiti nell'equazione gaussiana per lenti sottili:
1 / f = 1 / p + 1 / q
E ottieni:
1 / -40 = 1/40 + 1 / q
Da dove q = - 20 cm
Successivamente, sostituiamo il risultato ottenuto in precedenza nell'equazione con l'ingrandimento di una lente:
M = - q / p = - -20 / 40 = 0,5
Ottenendo che il valore dell'incremento sia:
M = h '/ h = 0,5
Risolvendo per h ', che è il valore dell'altezza dell'immagine, otteniamo:
h '= h / 2 = 2,5 cm.
L'altezza dell'immagine è di 2,5 cm. Inoltre, l'immagine è diritta poiché M> 0 e diminuita poiché il valore assoluto di M è inferiore a 1.
Riferimenti
- Leggero (n.d.). Su Wikipedia. Estratto l'11 aprile 2019 da es.wikipedia.org.
- Lekner, John (1987). Teoria della riflessione, delle onde elettromagnetiche e delle particelle. Springer.
- Leggero (n.d.). In Wikipedia. Estratto l'11 aprile 2019 da en.wikipedia.org.
- Obiettivo (n.d.). Su Wikipedia. Estratto l'11 aprile 2019 da es.wikipedia.org.
- Obiettivo (ottica). In Wikipedia. Estratto l'11 aprile 2019 da en.wikipedia.org.
- Hecht, Eugene (2002). Ottica (4a ed.). Addison Wesley.
- Tipler, Paul Allen (1994). Fisico. 3a edizione. Barcellona: ho invertito.



Nessun utente ha ancora commentato questo articolo.