
Caratteristiche della funzione costante, esempi, esercizi
Il funzione costante è quello in cui il valore di y è mantenuto costante. In altre parole: una funzione costante ha sempre la forma f (x) = k, dove K è un numero reale.
Quando si traccia graficamente la funzione costante nel sistema di coordinate xy, si traduce sempre in una linea retta parallela all'asse orizzontale o all'asse del X.
Questa funzione è un caso particolare di funzione affine, il cui grafico è anche una linea retta, ma con una pendenza. La funzione costante ha pendenza zero, cioè è una linea orizzontale, come mostrato nella figura 1.
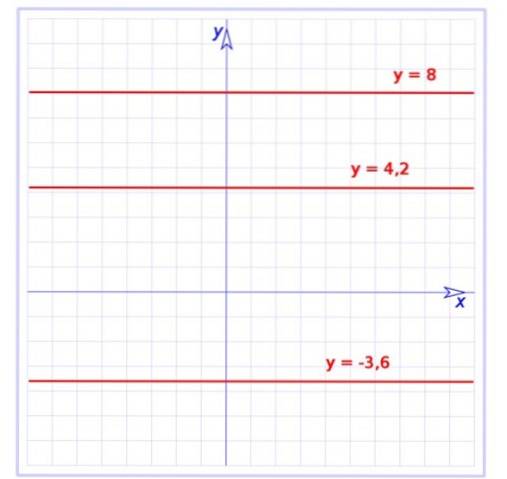
Qui viene mostrato il grafico di tre funzioni costanti:
f (x) = -3,6
g (x) = 4,2
h (x) = 8
Sono tutte linee parallele all'asse orizzontale, la prima è sotto detto asse, mentre le altre sono sopra.
Indice articolo
- 1 Caratteristiche della funzione costante
- 2 esempi
- 2.1 Un altro modo per rappresentare una funzione costante
- 3 esercizi risolti
- 3.1 - Esercizio 1
- 3.2 - Esercizio 2
- 3.3 - Esercizio 3
- 3.4 - Esercizio 4
- 3.5 - Esercizio 6
- 4 Riferimenti
Caratteristiche della funzione costante
Possiamo riassumere le principali caratteristiche della funzione costante come segue:
-Il suo grafico è una linea orizzontale retta.
-Ha un'unica intersezione con l'asse Y, di valore K.
-È continuo.
-Il dominio della funzione costante (l'insieme di valori che il X) è l'insieme dei numeri reali R.
-Il percorso, l'intervallo o il controdominio (l'insieme di valori che la variabile assume Y) è semplicemente la costante K.
Esempi
Le funzioni sono necessarie per stabilire collegamenti tra quantità che dipendono l'una dall'altra in qualche modo. La relazione tra loro può essere modellata matematicamente, per scoprire come si comporta l'una quando l'altra varia..
Questo aiuta a costruire modelli per molte situazioni e fare previsioni sul loro comportamento ed evoluzione..
Nonostante la sua apparente semplicità, la funzione costante ha molte applicazioni. Ad esempio, quando si tratta di studiare grandezze che rimangono costanti nel tempo, o almeno per un tempo apprezzabile.
In questo modo, le grandezze si comportano in situazioni come le seguenti:
-Il velocità guidare un'auto in movimento lungo una lunga autostrada rettilinea. Finché non si frena o si accelera, l'auto ha un movimento rettilineo uniforme.

-Un condensatore completamente carico scollegato da un circuito ha a caricare costante nel tempo.
-Infine, un parcheggio a tariffa forfettaria mantiene a prezzo costante, non importa per quanto tempo un'auto è parcheggiata lì.
Un altro modo per rappresentare una funzione costante
In alternativa, la funzione costante può essere rappresentata come segue:
f (x) = kx0
Poiché qualsiasi valore di X elevato a 0 dà come risultato 1, l'espressione precedente si riduce a quella già familiare:
f (x) = k
Ovviamente ciò accade finché il valore di K è diverso da 0.
Questo è il motivo per cui anche la funzione costante è classificata come a funzione polinomiale di grado 0, essendo l'esponente della variabile X è 0.
Esercizi risolti
- Esercizio 1
Rispondi alle seguenti domande:
a) Si può affermare che la retta data da x = 4 è una funzione costante? Motivo della tua risposta.
b) Una funzione costante può avere un'intercetta x?
c) La funzione f (x) = w è costanteDue?
Rispondi a
Ecco il grafico della linea x = 4:
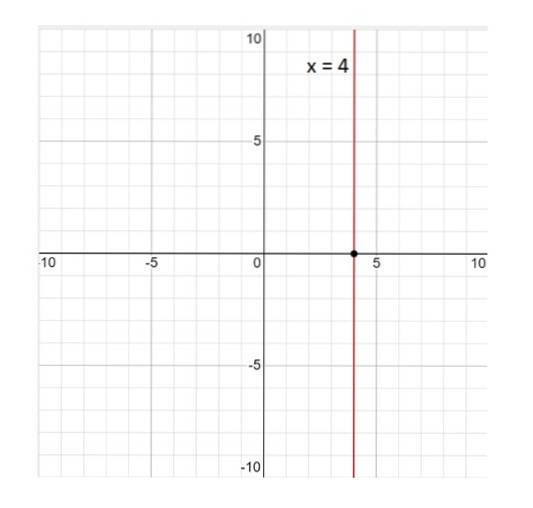
La linea x = 4 non è una funzione; per definizione una funzione è una relazione tale che ad ogni valore della variabile X corrisponde a un singolo valore di Y. E in questo caso questo non è vero, poiché il valore x = 4 è associato a infiniti valori di Y. Quindi la risposta è no.
Risposta b
In generale una funzione costante non ha intersezione con l'asse X, a meno che non si tratti di y = 0, in tal caso è l'asse X Detto correttamente.
Risposta c
Sì, da allora w è costante, così è il suo quadrato. Ciò che conta è questo w non dipendono dalla variabile di input X.
- Esercizio 2
Trova l'intersezione tra le funzioni f (x) = 5 Y g (x) = 5x - 2
Soluzione
Per trovare l'intersezione tra queste due funzioni, possono essere rispettivamente riscritte come:
y = 5; y = 5x - 2
Si equalizzano ottenendo:
5x - 2 = 5
Cos'è un'equazione lineare di primo grado, la cui soluzione è:
5x = 5 + 2 = 7
x = 7/5
Il punto di intersezione è (7 / 5,5).
- Esercizio 3
Mostra che la derivata di una funzione costante è 0.
Soluzione
Dalla definizione di derivata abbiamo:

f (x + h) = k
Sostituendo nella definizione:

Inoltre, se pensiamo al derivato come al tasso di variazione dy / dx, la funzione costante non subisce alcuna variazione, quindi la sua derivata è zero.
- Esercizio 4
Trova l'integrale indefinito di f (x) = k.
Soluzione

Una compagnia di telefoni cellulari offre un servizio Internet a tariffa fissa illimitata per $ 15 al mese. Qual è la funzione del prezzo in base al tempo?
Soluzione
Sia P il prezzo da pagare in $ et il tempo, che può essere espresso in giorni. La funzione è impostata in questo modo:
P (t) = 15
- Esercizio 6
Il grafico seguente della velocità rispetto al tempo corrisponde al movimento di una particella.

Chiede:
a) Scrivi un'espressione per la funzione di velocità in funzione del tempo v (t).
b) Trova la distanza percorsa dal cellulare nell'intervallo di tempo compreso tra 0 e 9 secondi.
Soluzione a
Dal grafico mostrato si può vedere che:
-v = 2 m / s nell'intervallo di tempo compreso tra 0 e 3 secondi
-Il cellulare viene fermato tra 3 e 5 secondi, poiché in questo intervallo la velocità è 0.
-v = - 3 m / s tra 5 e 9 secondi.
È un esempio di funzione a tratti, o funzione a tratti, che a sua volta è composta da funzioni costanti, valide solo per gli intervalli di tempo indicati. Si conclude che la funzione ricercata è:

Soluzione b
Dal grafico v (t) si può calcolare la distanza percorsa dal mobile, numericamente equivalente all'area sotto / sulla curva. In questo modo:
-Distanza percorsa tra 0 e 3 secondi = 2 m / s. 3 s = 6 m
-Tra 3 e 5 secondi è stato fermato, quindi non ha percorso alcuna distanza.
-Distanza percorsa tra 5 e 9 secondi = 3 m / s. 4 s = 12 m
In totale, il cellulare ha percorso 18 m. Si noti che sebbene la velocità sia negativa nell'intervallo tra 5 e 9 secondi, la distanza percorsa è positiva. Quello che succede è che durante quell'intervallo di tempo, il cellulare aveva cambiato il senso della sua velocità.
Riferimenti
- Geogebra. Funzioni costanti. Estratto da: geogebra.org.
- Maplesoft. La funzione costante. Estratto da: maplesoft.com.
- Wikibooks. Calcolo in una variabile / Funzioni / Funzione costante. Recupero da: es.wikibooks.org.
- Wikipedia. Funzione costante. Estratto da: en.wikipedia.org
- Wikipedia. Funzione costante. Estratto da: es.wikipedia.org.


Nessun utente ha ancora commentato questo articolo.