
Coefficiente di attrito statico, esempio, esercizio

Il Frizione statica è la forza che nasce tra due superfici quando una superficie non scorre rispetto all'altra. È di grande importanza, poiché ci permette di andare avanti camminando, poiché è la forza presente tra il pavimento e la suola delle scarpe.
È anche l'attrito statico che appare tra la pavimentazione e le gomme dell'auto. Se questa forza non è presente, allora è impossibile che l'auto si metta in movimento, come accade in un'auto che cerca di partire su una superficie ghiacciata: le ruote scivolano ma l'auto non si muove.

L'attrito statico dipende dalla rugosità delle superfici a contatto e anche dal tipo di materiale di cui sono costituite. Ecco perché gli pneumatici e le scarpe sportive sono in gomma, per aumentare l'attrito con la pavimentazione..
Nel modello ad attrito statico, le caratteristiche dei materiali e il grado di rugosità tra le superfici sono riassunte in un numero denominato coefficiente di attrito statico, che è determinato sperimentalmente.
Indice articolo
- 1 Coefficiente di attrito statico
- 2 Esempio: determinazione del coefficiente di attrito statico
- 3 Esercizio
- 3.1 Soluzione
- 4 Riferimenti
Coefficiente di attrito statico

La figura sopra mostra un libro che è fermo su un tavolo che ha un'inclinazione di 15.7º.
Se le superfici del libro e del tavolo fossero molto lisce e levigate, il libro non potrebbe stare fermo. Ma poiché non lo sono, appare una forza tangente alle superfici in contatto chiamata forza di Frizione statica.
Se l'angolo di inclinazione è abbastanza grande, non è sufficiente forza di attrito statico per bilanciare il libro e inizierebbe a scorrere.
In questo caso c'è anche attrito tra il libro e il tavolo, ma sarebbe a forza di attrito dinamico, chiamato anche attrito cinetico.
Esiste un confine tra attrito statico e attrito dinamico, che si verifica quando l'attrito statico raggiunge il suo valore massimo.
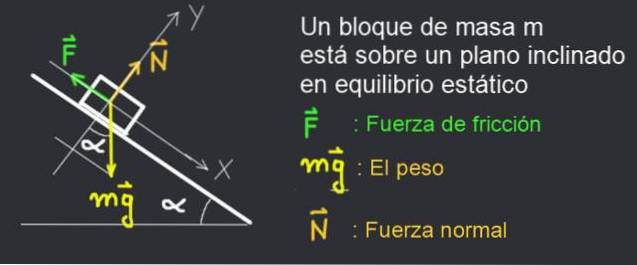
Consideriamo in figura 2 il diagramma delle forze di un libro di massa m mantenuto a riposo su un piano di inclinazione α.
Il libro rimane a riposo perché la forza di attrito statico F bilancia il sistema.
Se l'angolo di inclinazione aumenta leggermente, le superfici a contatto devono fornire una maggiore forza di attrito, ma la quantità di attrito statico che le superfici a contatto possono fornire ha un limite massimo Fmax, vale a dire:
F ≤ Fmax.
La massima forza di attrito statico dipenderà dai materiali e dal grado di rugosità delle superfici a contatto, nonché dalla fermezza dell'impugnatura.
Il coefficiente di attrito statico μe è un numero positivo che dipende dalle caratteristiche delle superfici a contatto. Forza normale N che il piano esercita sul blocco mostra il grado di tenuta tra la superficie del blocco e il piano. In questo modo determinano la massima forza di attrito che le superfici forniscono in assenza di scorrimento:
Fmax = μe N
In sintesi, la forza di attrito statico segue il seguente modello:
F ≤ μe N
Esempio: determinazione del coefficiente di attrito statico
Il coefficiente di attrito statico è un numero adimensionale determinato sperimentalmente per ogni coppia di superfici.
Consideriamo il blocco a riposo in figura 2. Su di esso agiscono le seguenti forze:
- Forza di attrito: F
- Il peso del blocco di massa m: mg
- Forza normale: N
Poiché il blocco è a riposo e non ha accelerazione, secondo la seconda legge di Newton, la forza risultante -una somma vettoriale- è zero:
F + N + mg = 0
Si considera un sistema di coordinate XY fisso con l'asse X lungo il piano inclinato e l'asse Y perpendicolare ad esso, come mostrato in figura 2.
Le forze devono essere separate secondo le loro componenti cartesiane, dando luogo al seguente sistema di equazioni:
-Componente X: -F + mg Sen (α) = 0
-Componente Y: N - mg Cos (α) = 0
Il valore della forza di attrito statico è risolto dalla prima equazione:
F = mg Sen (α)
E dal secondo il valore della forza normale:
N = mg Cos (α)
La forza di attrito statico F obbedisce al seguente modello:
F ≤ μe N
Sostituendo i valori ottenuti in precedenza nella disuguaglianza abbiamo:
mg Sen (α) ≤ μe mg Cos (α)
Tenendo conto che per valori di α compresi tra 0º e 90º, le funzioni seno e coseno sono entrambe positive e che il quoziente tra seno e coseno è la tangente, abbiamo:
Tan (α) ≤ μe
L'uguaglianza vale per un particolare valore di α chiamato angolo critico e che indichiamo con α *, ovvero:
μe = Tan (α *)
L'angolo critico viene determinato sperimentalmente, aumentando gradualmente l'inclinazione fino all'angolo retto al quale il blocco inizia a scorrere, ovvero l'angolo critico α *.
Nel libro della figura 1, questo angolo è stato determinato sperimentalmente risultando in 24 °. Quindi il coefficiente di attrito statico è:
μe = Tan (24º) = 0,45.
È un numero positivo compreso tra 0 e infinito. Se μe = 0 le superfici sono perfettamente lisce. Se μe → ∞ le superfici sono perfettamente unite o saldate.
In generale, il valore del coefficiente di attrito è compreso tra 0 e 10.
Esercizio
Nelle gare sprint o dragster, durante la partenza si ottengono accelerazioni fino a 4g, che si ottengono proprio quando le gomme non scivolano rispetto al pavimento..
Questo perché il coefficiente di attrito statico è sempre maggiore del coefficiente di attrito dinamico..
Supponendo che il peso totale del veicolo più il conducente sia di 600 kg e che le ruote posteriori supportino l'80% del peso, determinare la forza di attrito statico durante la partenza 4g e il coefficiente di attrito statico tra i pneumatici e la pavimentazione..

Soluzione
Secondo la seconda legge di Newton, la forza risultante è uguale alla massa totale del veicolo moltiplicata per l'accelerazione che acquisisce.
Poiché il veicolo è in equilibrio verticale, la normale e il peso si annullano, lasciando come forza risultante la forza di attrito F che la pavimentazione esercita sull'area di contatto delle ruote di trazione, lasciando che:
F = m (4g) = 600 kg (4 x 9,8 m / sDue) = 23520 N = 2400 kg-f
Ciò significa che la forza di trazione è di 2,4 tonnellate.
La forza di attrito che la ruota esercita sul terreno va all'indietro, ma la sua reazione, che è la stessa ed opposta, agisce sul pneumatico e va in avanti. Questa è la forza che guida il veicolo.
Naturalmente, tutta questa forza è prodotta dal motore che cerca di spingere il pavimento indietro attraverso la ruota, ma la ruota e il pavimento sono accoppiati dalla forza di attrito.
Per determinare il coefficiente di attrito statico utilizziamo il fatto che l'F ottenuto è il massimo attrito possibile, poiché siamo al limite della massima accelerazione, quindi:
F = μe N = μe (0,8 mg)
È stato preso in considerazione il fatto che le ruote motrici posteriori supportano 0,8 volte il peso. Risolvendo per il coefficiente di attrito, otteniamo:
μe = F / (0,8 mg) = 23520 N / (0,8 x 600 kg x 9,8 m / s ^ 2) = 5.
Conclusione: μe = 5.
Riferimenti
- Alonso M., Finn E. 1970. Physics volume I: Mechanics. Fondo interamericano per l'educazione S.A.
- Bauer, W. 2011. Fisica per l'ingegneria e le scienze. Volume 1. Mc Graw Hill.
- Hewitt, P. 2012. Scienze fisiche concettuali. Quinta edizione.
- Rex, A. 2011. Fondamenti di fisica. Pearson. 190-200.
- Giovane, Hugh. 2015. Fisica universitaria con fisica moderna. 14 ° Ed. Pearson.



Nessun utente ha ancora commentato questo articolo.