
Flusso volumetrico
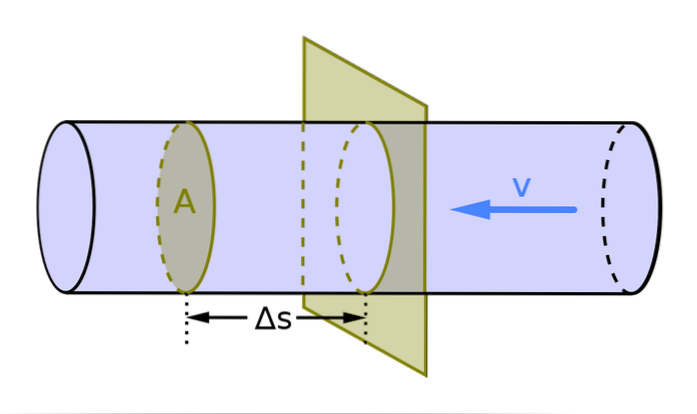
Cos'è il flusso volumetrico?
Il flusso volumetrico permette di determinare il volume del fluido che attraversa una sezione del condotto e fornisce una misura della velocità con cui il fluido si muove attraverso di esso. Pertanto, la sua misurazione è particolarmente interessante in campi diversi come l'industria, la medicina, l'edilizia e la ricerca, tra gli altri..
Tuttavia, misurare la velocità di un fluido (sia esso un liquido, un gas o una miscela di entrambi) non è semplice come misurare la velocità di spostamento di un corpo solido. Succede quindi che per conoscere la velocità di un fluido sia necessario conoscerne il flusso.
Questa e molte altre domande relative ai fluidi vengono affrontate dalla branca della fisica nota come meccanica dei fluidi. Il flusso è definito come quanto fluido passa attraverso una sezione di un condotto, sia esso un oleodotto, un oleodotto, un fiume, un canale, un condotto sanguigno, ecc., Prendendo in considerazione un'unità temporale.
Di solito viene calcolato il volume che attraversa una data area in un'unità di tempo, detto anche flusso volumetrico. Viene anche definito il flusso di massa o di massa che attraversa una data area in un momento specifico, sebbene sia usato meno frequentemente del flusso volumetrico..
Come viene calcolato il flusso volumetrico?
La portata volumetrica è rappresentata dalla lettera Q. Per i casi in cui il flusso si sposta perpendicolare alla sezione del conduttore, si determina con la seguente formula:
Q = A = V / t
In questa formula, A è la sezione del conduttore (è la velocità media del fluido), V è il volume et è il tempo. Poiché nel sistema internazionale l'area o la sezione del conduttore è misurata in mDue e la velocità in m / s, il flusso è misurato m3/ S.
Per i casi in cui la velocità di spostamento del fluido crea un angolo θ con la direzione perpendicolare alla sezione superficiale A, l'espressione per determinare la portata è la seguente:
Q = A cos θ
Ciò è coerente con l'equazione precedente, poiché quando il flusso è perpendicolare all'area A, θ = 0 e, quindi, cos θ = 1.
Le equazioni di cui sopra sono vere solo se la velocità del fluido è uniforme e se l'area della sezione è piatta. In caso contrario, la portata volumetrica viene calcolata tramite il seguente integrale:
Q = ∫∫S v d S
In questo integrale dS è il vettore di superficie, determinato dalla seguente espressione:
dS = n dS
Lì, n è il vettore unitario normale alla superficie del condotto e dS un elemento differenziale di superficie.
Equazione di continuità
Una caratteristica dei fluidi incomprimibili è che la massa del fluido viene conservata per mezzo di due sezioni. Per questo motivo è soddisfatta l'equazione di continuità che stabilisce la seguente relazione:
ρ1 PER1 V1 = ρDue PERDue VDue
In questa equazione ρ è la densità del fluido.
Per i casi di regimi in flusso permanente, in cui la densità è costante e, quindi, è vero che ρ1 = ρDue, si riduce alla seguente espressione:
PER1 V1 = ADue VDue
Ciò equivale ad affermare che il flusso è conservato e, quindi:
Q1 = QDue.
Dall'osservazione di quanto sopra ne consegue che i fluidi accelerano quando raggiungono una sezione più stretta di un condotto, mentre rallentano quando raggiungono una sezione più ampia di un condotto. Questo fatto ha interessanti applicazioni pratiche, poiché permette di giocare con la velocità di movimento di un fluido.
Principio di Bernoulli
Il principio di Bernoulli determina che per un fluido ideale (cioè un fluido che non ha né viscosità né attrito) che si muove in circolazione attraverso un condotto chiuso, la sua energia rimane costante durante tutto il suo spostamento..
In definitiva, il principio di Bernoulli non è altro che la formulazione della Legge di Conservazione dell'Energia per il flusso di un fluido. Pertanto, l'equazione di Bernoulli può essere formulata come segue:
h + vDue / 2g + P / ρg = costante
In questa equazione h è l'altezza eg è l'accelerazione dovuta alla gravità.
L'equazione di Bernoulli tiene conto dell'energia di un fluido in qualsiasi momento, un'energia composta da tre componenti.
- Una componente cinetica che include energia, dovuta alla velocità con cui si muove il fluido.
- Una componente generata dal potenziale gravitazionale, come conseguenza dell'altezza alla quale si trova il fluido.
- Un componente dell'energia di flusso, che è l'energia che un fluido possiede a causa della pressione.
In questo caso, l'equazione di Bernoulli è espressa come segue:
h ρ g + (vDue ρ) / 2 + P = costante
Logicamente, nel caso di un fluido reale l'espressione dell'equazione di Bernoulli non è soddisfatta, poiché nello spostamento del fluido si verificano perdite per attrito ed è necessario ricorrere ad un'equazione più complessa.
Cosa influenza il flusso volumetrico?
Il flusso volumetrico sarà influenzato se c'è un'ostruzione nel condotto.
Inoltre la portata volumetrica può variare anche per variazioni di temperatura e pressione nel fluido reale che si muove attraverso un condotto, soprattutto se si tratta di un gas, poiché il volume che un gas occupa varia in funzione della temperatura e della pressione a.
Metodo semplice per misurare il flusso volumetrico
Un metodo molto semplice per misurare il flusso volumetrico consiste nel far fluire un fluido in un serbatoio di misurazione per un periodo di tempo specificato..
Questo metodo generalmente non è molto pratico, ma la verità è che è estremamente semplice e molto illustrativo comprendere il significato e l'importanza di conoscere la portata di un fluido..
In questo modo, il fluido viene lasciato fluire in un serbatoio di misurazione per un periodo di tempo, viene misurato il volume accumulato e il risultato ottenuto viene diviso per il tempo trascorso.
Riferimenti
- Flusso (fluido) (n.d.). Su Wikipedia. Estratto da es.wikipedia.org.
- Portata volumetrica (n.d.). Su Wikipedia. Estratto da en.wikipedia.org.
- Engineers Edge, LLC. "Equazione della portata volumetrica del fluido". Ingegneri Edge
- Mott, Robert (1996). "1". Meccanica dei fluidi applicata (4a edizione). Messico: Pearson Education.
- Batchelor, G.K. (1967). Un'introduzione alla fluidodinamica. Cambridge University Press.
- Landau, L.D.; Lifshitz, E.M. (1987). Meccanica dei fluidi. Corso di Fisica Teorica (2a ed.). Pergamon Press.


Nessun utente ha ancora commentato questo articolo.