Si parla di esperimento casuale quando il risultato di ogni particolare processo è imprevedibile, anche se è possibile stabilire la probabilità che si verifichi un particolare risultato.
Tuttavia, dovrebbe essere chiarito che non è possibile riprodurre lo stesso risultato di un sistema casuale con gli stessi parametri e condizioni iniziali in ogni prova dell'esperimento..
Un buon esempio di esperimento casuale è il lancio di un dado. Anche se si prende cura di tirare il dado nello stesso modo, ogni tentativo produrrà un risultato imprevedibile. In realtà, l'unica cosa che si può dire è che il risultato può essere uno dei seguenti: 1, 2, 3, 4, 5 o 6.
Il lancio di una moneta è un altro esempio di un esperimento casuale con solo due possibili risultati: testa o croce. Sebbene la moneta venga lanciata dalla stessa altezza e nello stesso modo, il fattore di probabilità sarà sempre presente, con conseguente incertezza ad ogni nuovo tentativo..
L'opposto di un esperimento casuale è un esperimento deterministico. Ad esempio, è noto che ogni volta che l'acqua viene bollita a livello del mare, la temperatura di ebollizione è di 100 ºC. Ma non succede mai che, mantenendo le stesse condizioni, il risultato sia a volte 90 ºC, altre 12 0ºC e talvolta 100 ºC..
Indice articolo
Viene chiamato l'insieme di tutti i possibili risultati di un esperimento casuale spazio campione. Nell'esperimento casuale del lancio di un dado, lo spazio campionario è:
D = 1, 2, 3, 4, 5, 6.
D'altra parte, nel lancio di una moneta lo spazio campione è:
M = teste, timbro.
In un esperimento casuale, a evento è il verificarsi o meno di un certo risultato. Ad esempio, nel caso del lancio di una moneta, un evento o un evento è che esce testa.
Un altro evento in un esperimento casuale potrebbe essere il seguente: che un numero inferiore o uguale a tre viene tirato sul tiro di un dado.
Nel caso in cui si verifichi l'evento, l'insieme dei possibili risultati è l'insieme:
E = 1, 2, 3
A sua volta, questo è un sottoinsieme dello spazio campione o dell'insieme:
M = 1, 2, 3, 4, 5, 6.
Ecco alcuni esempi che illustrano quanto sopra:
Supponiamo che vengano lanciate due monete, una dopo l'altra. Chiede:
a) Indicare se si tratta di un esperimento casuale o, al contrario, di un esperimento deterministico.
b) Qual è lo spazio campionario S di questo esperimento?
c) Indicare l'insieme dell'evento A, corrispondente al fatto che l'esperimento risulta in testa e croce.
d) Calcola la probabilità che si verifichi l'evento A..
e) Infine, trova la probabilità che si verifichi l'evento B: nessuna testa appare nel risultato.
a) È un esperimento casuale perché non c'è modo di prevedere quale sarà il risultato di un lancio delle due monete.
b) Lo spazio campionario è l'insieme di tutti i possibili risultati:
S = (c, c), (c, s), (s, c), (s, s)
c) L'evento A, se si verifica, può avere i seguenti risultati:
A = (c, s), (s, c)
d) La probabilità che si verifichi l'evento A si ottiene dividendo il numero di elementi dell'insieme A per il numero di elementi dell'insieme S corrispondenti allo spazio campionario:
P (A) = 2/4 = ½ = 0,5 = 50%
e) L'insieme dei possibili esiti corrispondenti all'evento B (che non appare testa nell'esito) è:
B = (s, s)
Pertanto, la probabilità che l'evento B si verifichi in uno studio è il quoziente tra il numero di possibili esiti di B e il numero di casi totali:
P (B) = ¼ = 0,25 = 25%.
Una borsa contiene 10 biglie bianche e 10 biglie nere. Tre biglie consecutivamente vengono estratte dalla borsa a caso e senza guardare all'interno.
a) Determina lo spazio campionario di questo esperimento casuale.
b) Determinare l'insieme di risultati corrispondente all'evento A, che consiste nell'avere due biglie nere dopo l'esperimento.
c) L'evento B consiste nell'ottenere almeno due biglie nere, determinare l'insieme B dei risultati per questo evento.
d) Qual è la probabilità che si verifichi l'evento A.?
e) Trova la probabilità che si verifichi l'evento B..
f) Determina la probabilità che il risultato dell'esperimento casuale sia di avere almeno una biglia nera. Questo evento si chiamerà C.
Per costruire lo spazio campionario, è utile creare un diagramma ad albero, come quello mostrato in Figura 3:
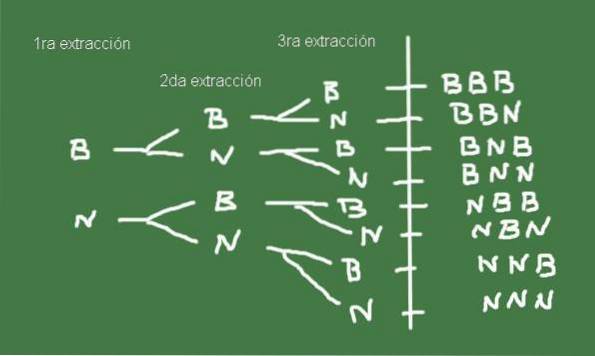
L'insieme Ω dei possibili risultati dell'estrazione di tre biglie da una borsa con lo stesso numero di biglie bianche e nere, è precisamente lo spazio campionario di questo esperimento casuale.
Ω = (b, b, b), (b, b, n), (b, n, b), (b, n, n), (n, b, b), (n, b, n) , (n, n, b), (n, n, n)
L'insieme dei possibili esiti corrispondenti all'evento A, che consiste nell'avere due biglie nere è:
A = (b, n, n), (n, b, n), (n, n, b)
L'Evento B è definito come: “avere almeno due biglie nere dopo averne estratte tre a caso”. L'insieme dei possibili risultati per l'evento B è:
B = (b, n, n), (n, b, n), (n, n, b), (n, n, n)
La probabilità di avere l'evento A è il quoziente tra il numero di possibili risultati per questo evento e il numero totale di possibili risultati, ovvero il numero di elementi nello spazio campionario.
P (A) = n (A) / n (Ω) = 3/8 = 0,375 = 37,5%
Quindi c'è una probabilità del 37,5% di avere due biglie nere dopo aver estratto a caso tre biglie dalla borsa. Ma nota che in nessun modo possiamo prevedere l'esatto risultato dell'esperimento.
La probabilità che si verifichi l'evento B, consistente nell'ottenere almeno una biglia nera è:
P (B) = n (B) / n (Ω) = 4/8 = 0,5 = 50%
Ciò significa che la possibilità che l'evento B si verifichi è uguale alla probabilità che non si verifichi.
La probabilità di ottenere almeno una biglia nera, dopo averne estratte tre, è pari a 1 meno la probabilità che il risultato sia "le tre biglie bianche".
P (C) = 1 - P (b b b) = 1 - ⅛ = ⅞ = 0,875 = 87,5%
Ora, possiamo controllare questo risultato, notando che il numero di possibilità in cui si verifica l'evento C è uguale al numero di elementi dei possibili risultati per l'evento C:
C = (b, b, n), (b, n, b), (b, n, n), (n, b, b), (n, b, n), (n, n, b) , (n, n, n)
n (C) = 7
P (C) = n (C) / n (Ω) = ⅞ = 87,5%
Nessun utente ha ancora commentato questo articolo.