Il Helmholtz free energy è un potenziale termodinamico che misura il lavoro utile di un sistema chiuso in condizioni di temperatura e volume costanti. L'energia libera di Helmholtz è indicata come F y è definita come la differenza dell'energia interna O meno prodotto della temperatura T per entropia S:
F = U - T⋅S
Poiché è energia, viene misurata in Joule nel Sistema Internazionale (SI), sebbene altre unità appropriate possano essere anche erg (CGS), calorie o elettron volt (eV).
La variazione negativa dell'energia di Helmholtz durante un processo è equiparata al lavoro massimo che il sistema può fare in un processo isocoro, cioè a volume costante. Quando il volume non viene mantenuto costante, parte di questo lavoro può essere svolto sull'ambiente.
In questo caso ci riferiamo a lavori in cui il volume non varia, come lavori elettrici: dW = Φdq, con Φ come potenziale elettrico eq come carica elettrica.
Se anche la temperatura è costante, l'energia di Helmholtz viene ridotta al minimo quando viene raggiunto l'equilibrio. Per tutto questo, l'energia di Helmholtz è particolarmente utile nei processi a volume costante. In questo caso hai:
- Per un processo spontaneo: ΔF < 0
- Quando il sistema è in equilibrio: ΔF = 0
- In un processo non spontaneo: ΔF> 0.
Indice articolo
Come affermato all'inizio, l'energia di Helmholtz è definita come "l'energia interna U del sistema, meno il prodotto della temperatura assoluta T del sistema, per l'entropia S del sistema":
F = U - T⋅S
È una funzione della temperatura T e del volume V. I passaggi per visualizzarlo sono i seguenti:
- Partendo dalla prima legge della termodinamica, l'energia interna U è correlata all'entropia S del sistema e al suo volume V per processi reversibili attraverso la seguente relazione differenziale:
dU = dQ - dW = TdS - PdV
Da ciò ne consegue che l'energia interna U è una funzione delle variabili S Y V, Quindi:
U = U (S, V)
- Ora prendiamo la definizione di F ed è derivato:
dF = dU - d (TS) = dU - TdS - SdT
- Sostituendo lì l'espressione differenziale ottenuta per dU nel primo passaggio, rimane:
dF = TdS - PoV - TdS - SdT = -SdT - PoV
- Infine, si conclude che F è una funzione della temperatura T e del volume V e può essere espresso come:
F = F (T, V)
L'energia di Helmholtz può essere applicata come criterio generale di spontaneità in sistemi isolati, ma prima è conveniente specificare alcuni concetti:
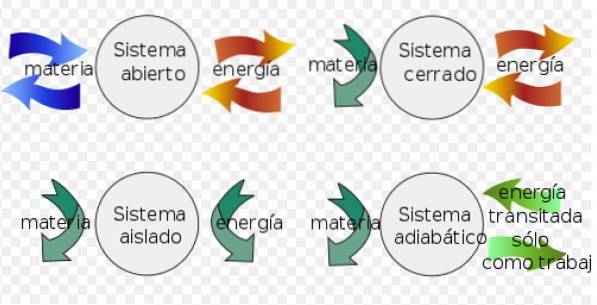
- UN sistema chiuso può scambiare energia con l'ambiente, ma non può scambiare materia.
- Invece a sistema isolato non scambia materia o energia con l'ambiente.
- Infine a sistema aperto scambiare materia ed energia con l'ambiente.
Nei processi reversibili, la variazione dell'energia interna viene calcolata come segue:
dU = TdS - PoV
Supponiamo ora un processo a volume costante (isocoro), in cui il secondo termine dell'espressione precedente ha contributo zero. Va inoltre ricordato che secondo il Disuguaglianza di Clausius:
dS ≥ dQ / T
Tale disuguaglianza si applica a un sistema termodinamico isolato.
Quindi per un processo (reversibile o meno) in cui il volume rimane costante, è vero quanto segue:
T dS ≥ dU (a volume fisso)
Tenendo conto che:
dF = dU - T dS
Avremo che in un processo isocoro a temperatura costante si accerta che: dF ≤ 0, come indicato all'inizio.
Quindi l'energia di Helmholtz F è una quantità decrescente in un processo spontaneo fintanto che è un sistema isolato. F raggiunge il suo valore minimo e stabile quando è stato raggiunto l'equilibrio reversibile.
Calcola la variazione dell'energia libera di Helmholtz F per 2 moli di gas ideale alla temperatura di 300K durante un'espansione isotermica che porta il sistema da un volume iniziale di 20 litri ad un volume finale di 40 litri.
Partendo dalla definizione di F:
F = U - T S
Allora una variazione finita di F, chiamata ΔF, sarà:
ΔF = ΔU - T ΔS
Poiché l'affermazione afferma che la temperatura è costante: ΔT = 0. Ora, nei gas ideali l'energia interna dipende solo dalla loro temperatura assoluta, ma poiché si tratta di un processo isotermico, allora ΔU = 0 Y ΔF = - T ΔS. Per i gas ideali, il cambiamento di entropia di un processo isotermico è scritto in questo modo:
ΔS = n.R.ln (VDue/ V1)
Applicando questa espressione:
ΔS = 2 moli x 8,314 J / (K mol) x ln (40L / 20L) = 11,53 J / K
Infine, il cambiamento nell'energia di Helmholtz è:
ΔF = - T ΔS = - 300K x 11,53 J / K = -3457,70 J.
All'interno di un cilindro c'è un pistone che lo divide in due sezioni e su ogni lato del pistone ci sono n moli di un gas ideale monoatomico, come mostrato nella figura sotto.
Le pareti del cilindro sono buoni conduttori di calore (diatermico) e sono a contatto con un serbatoio di temperatura To.
Il volume iniziale di ciascuna delle sezioni del cilindro è V1i e V2i, mentre i suoi volumi finali sono V1f e V2f dopo spostamento quasi statico. La movimentazione del pistone avviene tramite uno stantuffo che attraversa ermeticamente i due tappi dei cilindri.
Si chiede di trovare:
a) La variazione dell'energia interna del gas e il lavoro svolto dal sistema e
b) La variazione dell'energia di Helmholtz.
Poiché il pistone si muove quasi staticamente, la forza esterna applicata sul pistone deve bilanciare la forza dovuta alla differenza di pressione nelle due sezioni del cilindro..
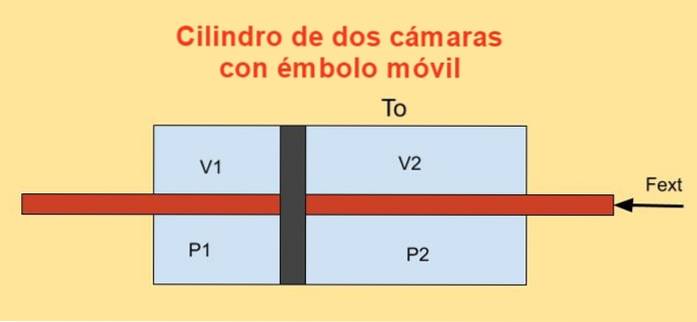
Il lavoro dW eseguito da forza esterna Fext durante uno spostamento infinitesimale dx è:
dW = - Fext dx = (P1 - PDue) a dx = P1 dV1 + PDue dVDue
Dove è stata utilizzata la relazione dV1 = - dVDue = a dx, essere per l'area dello stantuffo. D'altra parte, la variazione dell'energia di Helmholtz è:
dF = -SdT - PdV
Poiché la temperatura non cambia durante il processo, quindi dT = 0 Y dF = - PoV. Applicando questa espressione a ciascuna sezione del cilindro abbiamo:
dW = P1 dV1 + PDue dVDue = - dF1 - dFDue
Essere F1 Y FDue le energie di Helmholtz in ciascuna delle camere.
Il lavoro finito W può essere calcolato dalla variazione finita dell'energia di Helmholtz di ciascuna camera:
W = -ΔF1 - ΔFDue
Per trovare il cambiamento nell'energia di Helmholtz, viene utilizzata la definizione: F = U - T S. Come in ogni camera c'è un gas ideale monoatomico a temperatura costante To, l'energia interna non cambia (ΔU = 0), così che: ΔF = - To ΔS. Cosa c'è di più:
ΔS = nR ln (VF/Sega)
Che quando si sostituisce finalmente il lavoro svolto può essere:
W = -To nR ln (V1f / V1i) -A nR ln (V2f / V2i) = -ΔF1 -ΔFDue
W = - A nR ln [(V1f ⋅ V1i) / (V2f .V2i)] = - ΔFtotale
Essere ΔFtotale la variazione totale dell'energia di Helmholtz.
Nessun utente ha ancora commentato questo articolo.