Metodo di divisione sintetica ed esercizi risolti

Il divisione sintetica è un modo semplice per dividere qualsiasi polinomio P (x) per uno della forma d (x) = x - c. Ad esempio, il polinomio P (x) = (x⁵+3x⁴-7x³+2x^Due-8x + 1) può essere rappresentato come la moltiplicazione dei due polinomi più semplici (x + 1) e (x⁴ + 2x³).

È uno strumento molto utile poiché, oltre a permetterci di dividere i polinomi, ci permette anche di valutare un polinomio P (x) a qualsiasi numero c, che a sua volta ci dice con precisione se detto numero è zero o no del polinomio.

Grazie all'algoritmo di divisione, sappiamo che se abbiamo due polinomi P (x) Y d (x) non costanti, ci sono polinomi q (x) Y r (x) unici tali da ritenere che P (x) = q (x) d (x) + r (x), dove r (x) è zero o minore di q (x). Questi polinomi sono noti rispettivamente come quoziente e resto o resto.

Nelle occasioni in cui il polinomio d (x) è della forma x- c, la divisione sintetica ci dà un modo breve per trovare chi sono q (x) e r (x).

Indice articolo

• 1 Metodo di divisione sintetica
• 2 Esercizi risolti
  • 2.1 - Esempio 1
  • 2.2 - Esempio 2
  • 2.3 - Esempio 3
  • 2.4 - Esempio 4
• 3 Riferimenti

Metodo di divisione sintetica

Sia P (x) = a_nXⁿ+per_n-1X^n-1+... + A₁x + a₀ il polinomio che vogliamo dividere ed (x) = x-c il divisore. Per dividere per il metodo della divisione sintetica procediamo come segue:

1- Scriviamo i coefficienti di P (x) nella prima riga. Se una certa potenza di X non appare, mettiamo zero come coefficiente.

2- Nella seconda riga, a sinistra di a_n mettiamo c e disegniamo le linee di divisione come mostrato nella figura seguente:

3- Abbassiamo il coefficiente guida alla terza riga.

In questa espressione b_n-1= a_n

4- Moltiplichiamo c per il coefficiente direttivo b_n-1 e scriviamo il risultato nella seconda riga, ma una colonna a destra.

5- Aggiungiamo la colonna dove scriviamo il risultato precedente e posizioniamo il risultato sotto quella somma; cioè, nella stessa colonna, terza riga.

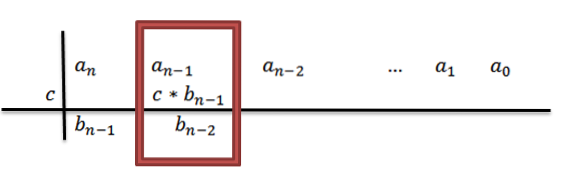
Quando si aggiunge, abbiamo come risultato_n-1+c * b_n-1, che per comodità chiameremo b_n-2

6- Moltiplichiamo c per il risultato precedente e scriviamo il risultato alla sua destra nella seconda riga.

7- Ripetiamo i passaggi 5 e 6 fino a raggiungere il coefficiente a₀.

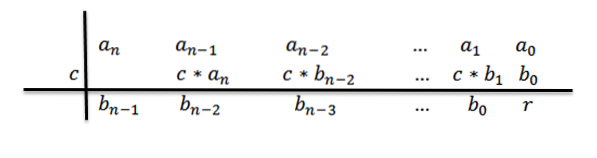
8- Scriviamo la risposta; cioè il quoziente e il resto. Poiché stiamo dividendo un polinomio di grado n per un polinomio di grado 1, abbiamo che il quoziente sarebbe di grado n-1.

I coefficienti del polinomio quoziente saranno i numeri nella terza riga tranne l'ultima, che sarà il resto o il resto della divisione.

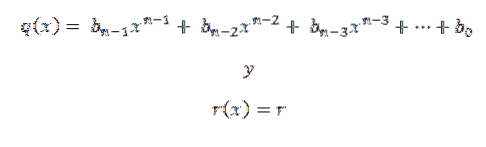
Esercizi risolti

- Esempio 1

Eseguire la seguente divisione con il metodo della divisione sintetica:

(X⁵+3x⁴-7x³+2x^Due-8x + 1): (x + 1).

Soluzione

Per prima cosa scriviamo i coefficienti dei dividendi come segue:

Quindi scriviamo c sul lato sinistro, nella seconda riga, insieme alle linee di divisione. In questo esempio c = -1.

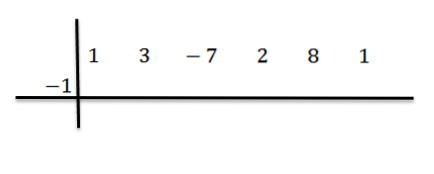
Abbassiamo il coefficiente principale (in questo caso b_n-1 = 1) e lo moltiplichiamo per -1:

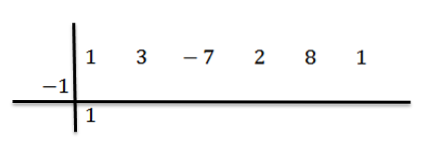
Scriviamo il suo risultato a destra nella seconda riga, come mostrato di seguito:

Aggiungiamo i numeri nella seconda colonna:

Moltiplichiamo 2 per -1 e scriviamo il risultato nella terza colonna, seconda riga:

Aggiungiamo nella terza colonna:

Procediamo allo stesso modo fino a raggiungere l'ultima colonna:

Quindi, abbiamo che l'ultimo numero ottenuto è il resto della divisione e i numeri rimanenti sono i coefficienti del polinomio quoziente. Questo è scritto come segue:

Se vogliamo verificare che il risultato sia corretto, è sufficiente verificare che sia vera la seguente equazione:

P (x) = q (x) * d (x) + r (x)

Quindi possiamo verificare che il risultato ottenuto sia corretto.

- Esempio 2

Eseguire la seguente divisione di polinomi con il metodo della divisione sintetica

(7x³-x + 2): (x + 2)

Soluzione

In questo caso abbiamo il termine x^Due non appare, quindi scriveremo 0 come coefficiente. Quindi, il polinomio sarebbe 7x³+0x^Due-x + 2.

Scriviamo i loro coefficienti di seguito, questo è:

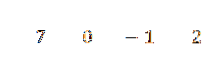
Scriviamo il valore di C = -2 sul lato sinistro nella seconda riga e tracciamo le linee di divisione.

Abbassiamo il coefficiente principale b_n-1 = 7 e moltiplicalo per -2, scrivendo il tuo risultato nella seconda riga a destra.

Aggiungiamo e procediamo come precedentemente spiegato, fino a raggiungere l'ultimo termine:

In questo caso, il resto è r (x) = - 52 e il quoziente ottenuto è q (x) = 7x^Due-14x + 27.

- Esempio 3

Un altro modo per usare la divisione sintetica è il seguente: supponiamo di avere un polinomio P (x) di grado ne di voler sapere qual è il valore valutandolo in x = c.

Con l'algoritmo di divisione abbiamo che possiamo scrivere il polinomio P (x) come segue:

In questa espressione q (x) e r (x) sono rispettivamente il quoziente e il resto. Ora, se d (x) = x- c, quando valutiamo in c nel polinomio otteniamo quanto segue:

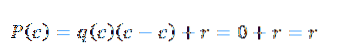
Per questo motivo non resta che trovare r (x), e possiamo farlo grazie alla divisione sintetica.

Ad esempio, abbiamo il polinomio P (x) = x⁷-9x⁶+19x⁵+12x⁴-3x³+19x^Due-37x-37 e vogliamo sapere qual è il suo valore valutandolo per x = 5. Per fare questo dividiamo tra P (x) ed (x) = x -5 con il metodo della divisione sintetica:

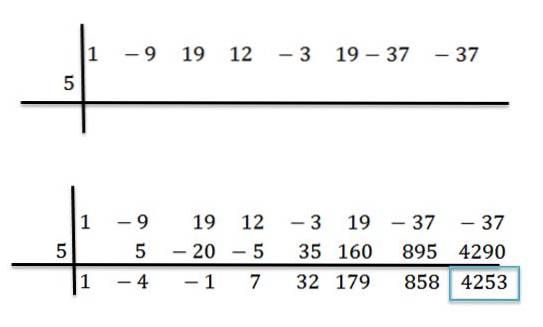
Terminate le operazioni, sappiamo che possiamo scrivere P (x) nel modo seguente:

P (x) = (x⁶-4x⁵ -X⁴+ 7x³ +32x^Due +179x + 858) * (x-5) + 4253

Pertanto, quando lo valutiamo dobbiamo:

P (5) = (5-4 (5) -5 + 7 (5) +32 (5) +179 (5) +858) * (5-5) + 4253

P (5) = (5-4 (5) -5 + 7 (5) +32 (5) +179 (5) +858) * (0) + 4253

P (5) = 0 + 4253 = 4253

Come possiamo vedere, è possibile utilizzare la divisione sintetica per trovare il valore di un polinomio valutandolo in c invece di sostituire semplicemente c con x. 

Se provassimo a valutare P (5) in modo tradizionale, saremmo costretti a eseguire alcuni calcoli che tendono a diventare noiosi.

- Esempio 4

L'algoritmo di divisione per i polinomi vale anche per i polinomi con coefficienti complessi e, di conseguenza, abbiamo che il metodo di divisione sintetica funziona anche per tali polinomi. Successivamente vedremo un esempio.

Useremo il metodo della divisione sintetica per mostrare che z = 1+ 2i è uno zero del polinomio P (x) = x³+ (1 + i) x^Due -(1 + 2i) x + (15 + 5i); ovvero, il resto della divisione P (x) per d (x) = x - z è uguale a zero.

Procediamo come prima: nella prima riga scriviamo i coefficienti di P (x), poi nella seconda scriviamo z e disegniamo le linee di divisione.

Eseguiamo la divisione come prima; questo è:

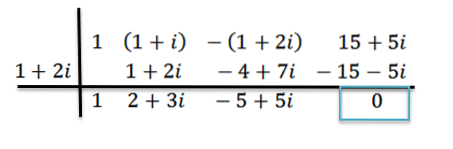
Possiamo vedere che il resto è zero; quindi, concludiamo che, z = 1+ 2i è uno zero di P (x).

Riferimenti

1. Baldor aurelio. Algebra. Grupo Editorial Patria.
2. Demana, Waits, Foley e Kennedy. Precalcolo: grafico, numerico, algebrico 7 ° Ed. Pearson Education.
3. Flemming W & Varserg D. Algebra e trigonometria con geometria analitica. Prentice Hall
4. Michael Sullivan. Precalculation 4a Ed. Pearson Education.
5. Rosso. Armando O. Algebra 1 6a ed. L'Ateneo.