
Caratteristiche di distribuzione uniforme continua, esempi, applicazioni
Una variabile casuale ha un'estensione distribuzione uniforme continua se la probabilità che assume un valore, all'interno di un intervallo finito [a, b], è la stessa per ogni sottointervallo di uguale lunghezza.
Questa distribuzione è analoga alla distribuzione discreta uniforme, che assegnava la stessa probabilità a ciascun risultato dell'esperimento casuale, ma in questo caso la variabile da considerare è continua. Ad esempio, l'esperimento che consiste nel selezionare un numero reale a caso, tra i valori aeb, segue la distribuzione uniforme. Ecco il suo grafico:
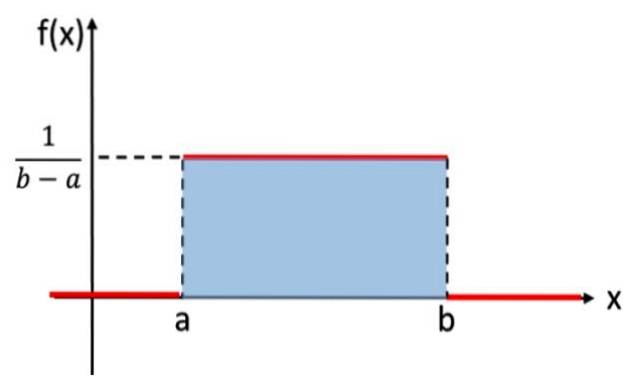
Nella notazione matematica, la distribuzione uniforme continua ha una funzione di densità definita come funzione a tratti o a tratti, che può essere scritta come:
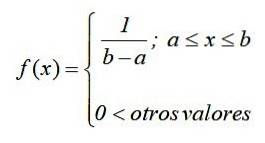
Il grafico di questa funzione, noto come curva o funzione di densità, è un rettangolo, quindi la distribuzione uniforme continua è anche nota come layout rettangolare y è la più semplice delle distribuzioni continue.
L'area sotto il grafico di una distribuzione di probabilità è uguale a 1 e assume sempre valori positivi. La distribuzione uniforme soddisfa questi criteri. Non è necessario integrare direttamente per verificare che l'area sia 1, poiché l'area del rettangolo ombreggiato in Figura 1 può essere calcolata utilizzando la formula:
Area = base x altezza = (b - a) x [1 / (b - a)] = 1
Conoscere l'area sotto la curva di densità è molto importante, perché esiste una relazione tra l'area e la probabilità di accadimento di un evento, che per questa distribuzione è determinata nella sezione successiva.
Caratteristiche della distribuzione uniforme continua
La distribuzione uniforme continua è caratterizzata da:
Funzione densità
Sia X la variabile casuale continua, che appartiene all'intervallo [a, b], quindi:

Funzione di distribuzione
La funzione di distribuzione calcola la probabilità che la variabile casuale X assuma un valore x tra i possibili valori dell'intervallo [a, b]. Per una distribuzione continua, viene generalmente calcolato in questo modo:

Nel caso della distribuzione uniforme continua, detta probabilità F (x) è uguale all'area del rettangolo la cui base è (x-a) e la sua altezza è (b-a):

Matematicamente, se F (x) = Pr (X = x) la seguente funzione è stabilita in parti, in base al risultato precedente:

In questo modo si verifica quanto detto prima: la probabilità dipende solo dal valore di (x-a) e non dalla sua collocazione nell'intervallo [a, b]. Il grafico della funzione di distribuzione è:
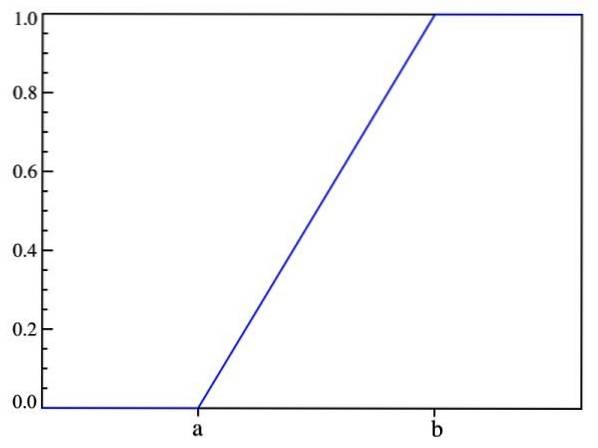
Valore atteso, varianza e deviazione standard
Dopo aver fatto numerosi esperimenti con la variabile casuale continua, viene chiamato il suo valore medio valore atteso, è indicato come E (X) ed è calcolato dal seguente integrale:

V (X) = E (XDue) - E (X)Due
Perciò:


D (X) = √ V (X)

Mediana, moda, simmetria e curtosi
Si può facilmente verificare che la mediana, che è il valore centrale della distribuzione uniforme, è uguale alla media, e poiché non esiste un valore che si ripeta più di altri, poiché tutti sono ugualmente probabili nell'intervallo [a, b] , la moda non esiste.
Per quanto riguarda la simmetria, la distribuzione uniforme è simmetrica e la curtosi, che è il grado di concentrazione dei valori attorno al centro, è -6/5.
Esempi
Varie situazioni possono essere modellate attraverso la distribuzione continua e quindi il loro comportamento può essere previsto. Ecco alcuni esempi:
Esempio 1
Un'azienda che fornisce il servizio elettrico fornisce livelli di tensioni distribuite uniformemente, comprese tra 123,0 V e 125,0 V. Ciò significa che nella presa domestica è possibile ottenere qualsiasi valore di tensione appartenente a quel range..
Quindi, come visto sopra, il grafico della funzione di densità è il rettangolo in rosso:

Calcolare la probabilità di avere una tensione all'interno dell'intervallo dato è molto semplice, ad esempio qual è la probabilità che l'azienda invii una tensione inferiore a 123,5 V?
Questa probabilità è uguale all'area del rettangolo ombreggiato in blu:
P (X<123.5) = (123.5 −123.0)x 0.5 = 0.25
E qual è la probabilità che la tensione erogata sia maggiore di 124,0 V.?
Poiché l'area totale è uguale a 1, la probabilità ricercata è:
P (X> 124,0 V) = 1 - (1 × 0,5) = 0,5
Ha senso, poiché 124.0 è esattamente il valore al centro dell'intervallo.
Esempio 2
Una certa variabile casuale X ha una distribuzione uniforme nell'intervallo [0,100]. Decidere:
a) La probabilità che il valore di X sia inferiore a 22.
b) La probabilità che X assuma valori compresi tra 20 e 35.
c) Il valore atteso, la varianza e la deviazione standard di questa distribuzione.
Rispondi a
È determinato in modo simile all'esempio precedente, ma prima dobbiamo determinare l'altezza del rettangolo, ricordando che l'area totale deve essere uguale a 1:
Area = 100 × altezza = 1
Pertanto il rettangolo ha un'altezza pari a 1/100 = 0,01
P (X<22) = 22×0.01 = 0.22
Risposta b
La probabilità richiesta è uguale all'area del rettangolo la cui larghezza è (35-20) e la cui altezza è 0,01:
P (22
Se preferisci andare direttamente alla funzione di distribuzione data sopra, devi solo sostituire i valori in:
P (20≤X≤35) = F (35) -F (20)
Con F (x) dato da:
F (x) = (x-a) / (b-a)
I valori da inserire sono:
a = 0
b = 100
F (35) = (35-0) / (100-0) = 0,35
F (20) = (20-0) / (100-0) = 0,20
P (20≤X≤35) = 0,35-0,20 = 0,15
Risposta c
Il valore atteso è:
E (X) = (a + b) / 2 = (100 + 0) / 2 = 50
La varianza è:
V (X) = (b-a)Due/ 12 = (100-0)Due/ 12 = 833,33
E la deviazione standard è:
D (X) = √833,33 = 28,87
Applicazioni
Questa distribuzione è utile quando si eseguono processi di simulazione statistica o quando si lavora su eventi la cui frequenza di accadimento è regolare..
Generazione di numeri casuali
Alcuni linguaggi di programmazione generano numeri casuali compresi tra 0 e 1 e, come si può vedere dagli esempi precedenti, la distribuzione di probabilità seguita è uniforme. In questo caso, l'intervallo da considerare è [0,1].
Campionamento di distribuzioni arbitrarie
Se hai un esperimento in cui gli eventi hanno regolarità, come spiegato prima, puoi, in linea di principio, assegnare a ciascuno la stessa probabilità di accadimento. In questo caso, il modello probabilistico di distribuzione uniforme fornisce informazioni per l'analisi..
Arrotondare gli errori
La distribuzione uniforme viene utilizzata anche per arrotondare le differenze tra i valori osservati ei valori reali di una variabile, assumendo una distribuzione uniforme dell'errore in un dato intervallo, secondo l'arrotondamento, solitamente da -0,5 a +0,5.
Riferimenti
- Berenson, M. 1985. Statistiche per la gestione e l'economia. Interamericana S.A.
- Canavos, G. 1988. Probabilità e statistica: applicazioni e metodi. Mcgraw hill.
- Devore, J. 2012. Probabilità e statistica per l'ingegneria e la scienza. 8 °. Edizione. Cengage.
- Levin, R. 1988. Statistics for Administrators. 2 °. Edizione. Prentice Hall.
- Triola, M. 2010. Statistica elementare. 11 °. Edizione. Addison Wesley.
- Walpole, R. 2007. Probabilità e statistica per l'ingegneria e le scienze. Pearson.


Nessun utente ha ancora commentato questo articolo.