
Derivata del calcolo cotangente, dimostrazione, esercizi
Il derivato della cotangente è uguale al contrario del quadrato della cosecante "-CscDue". Questa formula obbedisce alle leggi della derivata per definizione e alla differenziazione delle funzioni trigonometriche. È indicato come segue:
d (ctg u) = -cscDue o . du
Dove "du" simboleggia l'espressione derivata dalla funzione argomento, rispetto alla variabile indipendente.

Indice articolo
- 1 Come viene calcolato?
- 2 Caratteristiche della funzione cotangente
- 2.1 Asintoti verticali
- 2.2 Dominio
- 2.3 Gamma
- 2.4 Frequenza
- 2.5 Comportamento
- 3 Demo
- 3.1 Prova differenziale trigonometrica
- 3.2 Dimostrazione per definizione di derivata
- 4 Esercizi risolti
- 4.1 Esercizio 1
- 4.2 Esercizio 2
- 5 Riferimenti
Come viene calcolato?
La procedura per sviluppare questi derivati è abbastanza semplice. Tutto quello che devi fare è identificare correttamente l'argomento e il tipo di funzione che rappresenta..
Ad esempio, l'espressione Ctg (f / g) ha una divisione nel suo argomento. Ciò richiederà una differenziazione rispetto a U / V, dopo aver sviluppato la derivata della cotangente.
La cotangente è il reciproco della tangente. Algebricamente questo significa che:
(1 / tg x) = ctg x
Ctg x = Cos x / Sen x
Non è corretto affermare che la funzione cotangente è l '"inversa" della tangente. Questo perché la funzione tangente inversa per definizione è tangente all'arco.
(Tg-1 x) = arctg x
Secondo la trigonometria pitagorica, la cotangente è coinvolta nelle seguenti sezioni:
Ctg x = (cos x) / (sin x)
CtgDue x + 1 = CscDue X
Secondo la trigonometria analitica, risponde alle seguenti identità:
Ctg (a + b) = (1 - tg a. Tg b) / (tg a + tg b)
Ctg (a - b) = (1 + tg a. Tg b) / (tg a - tg b)
Ctg (2a) = (1 - tgDue a) / (2tg a)
Caratteristiche della funzione cotangente
Occorre analizzare diverse caratteristiche della funzione f (x) = ctg x per definire gli aspetti necessari per studiarne la differenziabilità e l'applicazione.
Asintoti verticali
La funzione cotangente non è definita sui valori che rendono zero l'espressione "Senx". A causa del suo equivalente Ctg x = (cos x) / (sin x), avrà un'indeterminatezza in tutti i "nπ" con n appartenenti agli interi.
Cioè, in ciascuno di questi valori di x = nπ ci sarà un asintoto verticale. Man mano che ti avvicini da sinistra il valore della cotangente diminuirà rapidamente e man mano che ti avvicini da destra, la funzione aumenterà indefinitamente.
Dominio
Il dominio della funzione cotangente è espresso dall'insieme x ∈ R / x ≠ nπ, n ∈ Z. Questo viene letto come "x appartenente all'insieme dei numeri reali tale che x è diverso da nπ, con n appartenente all'insieme degli interi".
Rango
L'intervallo della funzione cotangente va da meno a più infinito. Pertanto si può concludere che il suo intervallo è l'insieme dei numeri reali R.
Frequenza
La funzione cotangente è periodica e il suo periodo è uguale a π. In questo modo viene soddisfatta l'uguaglianza Ctg x = Ctg (x + nπ), dove n appartiene a Z.
Comportamento
È una funzione dispari, poiché Ctg (-x) = - Ctg x. In questo modo è noto che la funzione presenta una simmetria rispetto all'origine delle coordinate. Presenta anche una diminuzione in ogni intervallo situato tra 2 successivi asintoti verticali.
Non ha valori massimi o minimi, perché le sue approssimazioni agli asintoti verticali presentano comportamenti dove la funzione aumenta o diminuisce indefinitamente.
Gli zeri o le radici della funzione cotangente si trovano a multipli dispari di π / 2. Ciò significa che Ctg x = 0 vale per i valori della forma x = nπ / 2 con n numeri interi dispari.
Dimostrazione
Esistono 2 modi per dimostrare la derivata della funzione cotangente.
Prova differenziale trigonometrica
Viene dimostrata la derivata della funzione cotangente dal suo equivalente in seno e coseno.
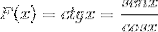
Viene considerato come la derivata di una divisione di funzioni
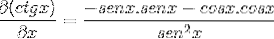
Dopo la derivazione i fattori vengono raggruppati e lo scopo è quello di emulare le identità pitagoriche
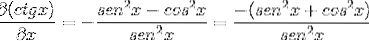
Sostituendo le identità e applicando la reciprocità, si ottiene l'espressione
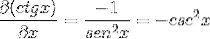
Dimostrazione per definizione di derivata
La seguente espressione corrisponde alla derivata per definizione. Dove la distanza tra 2 punti della funzione si avvicina a zero.
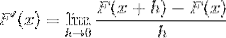
Sostituendo la cotangente abbiamo:
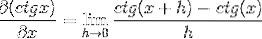
Le identità vengono applicate per la somma di argomenti e reciprocità
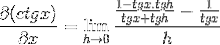
La frazione del numeratore è tradizionalmente gestita
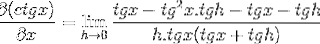
Eliminando gli elementi opposti e prendendo un fattore comune, otteniamo
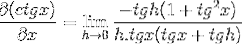
Applicando identità pitagoriche e reciprocità dobbiamo
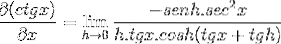
Gli elementi valutati in x sono costanti rispetto al limite, quindi possono lasciare l'argomento di questo. Quindi vengono applicate le proprietà dei limiti trigonometrici.
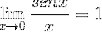
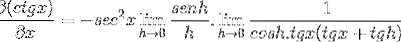
Il limite viene valutato
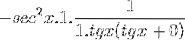
Quindi viene scomposto fino a raggiungere il valore desiderato
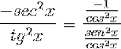
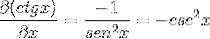
La derivata della cotangente è così dimostrata come l'opposto del quadrato della cosecante.
Esercizi risolti
Esercizio 1
In base alla funzione f (x), definire l'espressione f '(x)
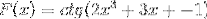
La derivazione corrispondente viene applicata rispettando la regola della catena
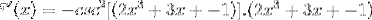
Derivare l'argomento
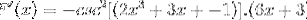
A volte è necessario applicare identità reciproche o trigonometriche per adattare le soluzioni.
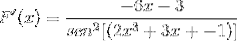
Esercizio 2
Definisci l'espressione differenziale corrispondente a F (x)
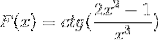
Secondo la formula di derivazione e rispettando la regola della catena
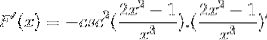
L'argomento è derivato, mentre il resto rimane lo stesso
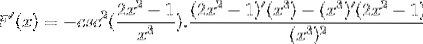
Derivare tutti gli elementi
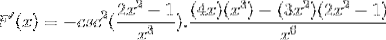
Operando in modo tradizionale i prodotti della stessa base
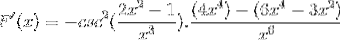
Gli elementi uguali vengono aggiunti e il fattore comune viene estratto
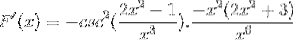
I segni sono semplificati e gestiti. Dare modo a un'espressione completamente derivata
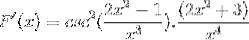
Riferimenti
- Serie trigonometrica, volume 1. A. Zygmund. Cambridge University Press, 2002
- Calcolo di una singola variabile. Ron Larson, Bruce H. Edwards. Cengage Learning, 10 novembre 2008
- Calcolo con trigonometria e geometria analitica. John H. Saxon, John Saxon, Frank Wang, Diana Harvey. Editori sassoni, 1988
- Analisi multivariabile. Satish Shirali, Harkrishan Lal Vasudeva. Springer Science & Business Media, 13 dicembre. 2010
- Dinamica dei sistemi: modellazione, simulazione e controllo di sistemi meccatronici. Preside C. Karnopp, Donald L. Margolis, Ronald C. Rosenberg. John Wiley & Sons, 7 marzo 2012
- Calcolo: matematica e modellazione. William Bauldry, Joseph R. Fiedler, Frank R. Giordano, Ed Lodi, Rick Vitray. Addison Wesley Longman, 1 gennaio 1999



Nessun utente ha ancora commentato questo articolo.