Corpo rigido

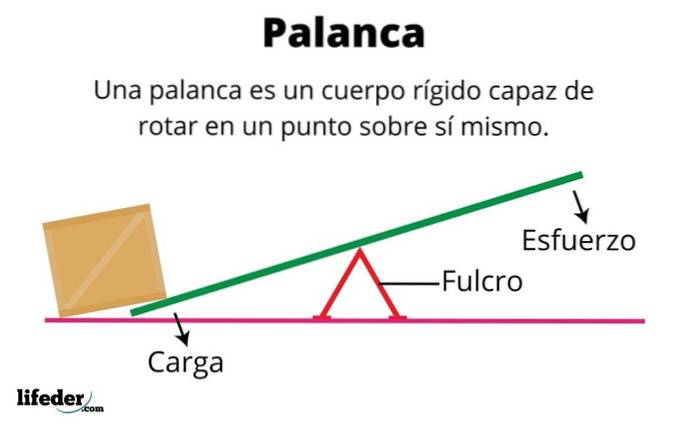
Cos'è un corpo rigido?

Un corpo rigido è un oggetto materiale le cui particelle rimangono sempre nelle stesse posizioni relative. Pertanto, è un oggetto che non si deforma, una qualità attribuita alle forti forze di coesione che tengono in posizione le particelle..

In realtà, le particelle di qualsiasi corpo sottoposto a forze esterne tendono a vibrare o muoversi, quindi l'oggetto si deforma sempre in una certa misura, ma questi effetti sono generalmente piccoli.

Quando questo è il caso, si può presumere che il corpo sia rigido e abbia un'ottima approssimazione del suo comportamento, anche se si tratta di un'idealizzazione.

Tipi di corpo rigido

Si possono distinguere due tipi di carrozzeria rigida:

• Quelle le cui particelle arrivano in quantità discrete, cioè possono essere contate. Ad esempio, due sfere metalliche unite da un'asta sottile e leggera possono essere considerate come un'unica entità. Se l'asta è abbastanza rigida da non piegarsi, il sistema è considerato un corpo rigido.
• Quelle continue, il che significa che le particelle che le compongono sono indistinguibili. Gli oggetti di uso quotidiano e la natura sono buoni esempi: pietre, mobili e altri, così come la Terra e altri corpi celesti rocciosi.

Movimento e dinamica del corpo rigido

Come gli oggetti considerati come particelle, i corpi rigidi possono traslare, ruotare e avere un movimento più generale, combinando traslazione e rotazione.

Per studiare la traslazione non è necessario analizzare separatamente il movimento di ogni particella, ma piuttosto il movimento del centro di massa, punto in cui si considera che tutta la massa dell'oggetto sia concentrata..

Questi movimenti di traslazione e rotazione possono essere:

• Indipendente, come nel caso dei pianeti, che hanno un movimento rotatorio attorno al proprio asse (considerato fisso) e un movimento di traslazione attorno al Sole, ma le velocità di ciascuno non sono correlate..
• Roto-traslazione, se la velocità angolare e la velocità di traslazione del centro di massa sono correlate. In questo caso l'asse di rotazione è mobile, come nel caso del cilindro che rotola su un ripido pendio senza scivolare..

La dinamica del corpo rigido

Le seguenti grandezze sono rilevanti nella dinamica del corpo rigido:

Centro di massa

Il centro di massa è il punto in cui si considera concentrata tutta la massa del corpo. Se è un corpo omogeneo e simmetrico, come una sfera, il centro di massa coincide con il centro geometrico.

Momento d'inerzia

Questa grandezza scalare è il valore dell'inerzia rotazionale o della resistenza a cui un oggetto si oppone per ruotare attorno a un certo asse. Dipende interamente dalla geometria dell'oggetto e dalla sua massa e quindi, in alcuni casi, è più facile ruotare attorno a certi assi rispetto ad altri..

Per corpi dalle forme geometriche ben definite, esistono tabelle con i momenti di inerzia rispetto agli assi di simmetria, ad esempio quello che passa per il centro di massa. Con queste informazioni ed i teoremi relativi al momento d'inerzia si possono facilmente calcolare i momenti sugli altri assi..

Forze e coppia o coppia

Ci vogliono forze per muovere un corpo. Se il centro di massa del solido rigido viene traslato, l'equazione del moto, secondo la seconda legge di Newton, è:

F_netto = M ∙per_cm

Dove:

-La forza netta è F_netto

-M è la massa

-L'accelerazione del centro di massa è per_cm

Tuttavia, non tutte le forze applicate riescono a far ruotare l'oggetto. Ciò richiede la coppia o coppia, che indica quanto sia efficace l'azione di rotazione di una forza. È definito come il prodotto vettoriale tra il vettore di posizione r rispetto a un certo punto O e la forza F in questione. È indicato dalla lettera greca τ (in grassetto, poiché è anche un vettore):

τ = r × F

Nel Sistema Internazionale SI, l'unità per la coppia è N⋅m (newton per metro).

In molti casi, il movimento rotatorio attorno a un asse attraverso il centro di massa è descritto da un'equazione analoga alla seconda legge di Newton:

Energia cinetica di un solido rigido

Il movimento di un corpo rigido è descritto dalle traslazioni del centro di massa e dalle rotazioni attorno a quel punto, quindi la sua energia cinetica ha entrambi i contributi.

Sia K l'energia cinetica del corpo, v_cm la velocità del centro di massa, M la massa del corpo, I_cm il suo momento di inerzia rispetto al centro di massa e ω la velocità angolare. Si può dimostrare che l'energia cinetica è:

K = ½ Mv_cm^Due + ½ I_cm ω^Due

Si osserva che il secondo termine a destra è l'analogo rotazionale del termine a sinistra. Lì il momento di inerzia gioca lo stesso ruolo della massa, mentre la velocità angolare ha lo stesso ruolo della velocità lineare..

Esempi nella vita di tutti i giorni

Pendolo fisico

Il pendolo fisico o pendolo reale è molto facile da costruire: è costituito da un solido rigido come un'asta o una barra, che oscilla liberamente attorno ad un asse orizzontale. L'asse di rotazione non passa per il centro di massa dell'oggetto e questo in linea di principio può avere qualsiasi forma.

Questo pendolo differisce dal pendolo semplice, perché in quest'ultimo la massa che lo compone è considerata puntuale.

Ruota di bicicletta

Un altro esempio di scocca rigida ben nota è la ruota di bicicletta, il cui asse passa per il baricentro, che passa per il centro della ruota. Finché non si inclina di lato o non si gira, per descrivere il suo movimento si applicano le equazioni dinamiche sopra descritte..

Una palla da bowling

Il modello solido rigido è adatto per descrivere il movimento della palla da bowling sulla pista o quando rotola senza scivolare lungo la rampa di ritorno.

Lo yoyo

Questo popolare giocattolo è realizzato con un cilindro di legno o di plastica e una corda avvolta in una scanalatura che lo circonda..

Il cilindro può essere modellato come un corpo rigido in cui la tensione nella corda fornisce la coppia per la svolta, mentre il peso (applicato al baricentro) e la tensione sono responsabili dell'accelerazione verticale del baricentro..

Riferimenti

1. Bauer, W. 2011. Fisica per l'ingegneria e le scienze. Volume 1. Mc Graw Hill. 
2. Giancoli, D. 2006. Fisica: principi con applicazioni. 6 °. Ed prentice hall.
3.  Katz, D. 2013. Fisica per scienziati e ingegneri. Fondamenti e connessioni. Cengage Learning.
4. Sears, Zemansky. 2016. Fisica universitaria con fisica moderna. 14th. Ed. Volume 1. Pearson.
5. Serway, R., Jewett, J. (2008). Fisica per la scienza e l'ingegneria. Volume 1. 7th. Ed. Cengage Learning.