Il coordinate rettangolari o cartesiani sono quelli che si ottengono proiettando ortogonalmente sui tre assi cartesiani X, Y, Z un punto situato nello spazio tridimensionale.
Gli assi cartesiani sono linee reciprocamente orientate perpendicolari tra loro. Nel sistema di coordinate cartesiane, a ogni punto nello spazio vengono assegnati tre numeri reali che sono le sue coordinate rettangolari.
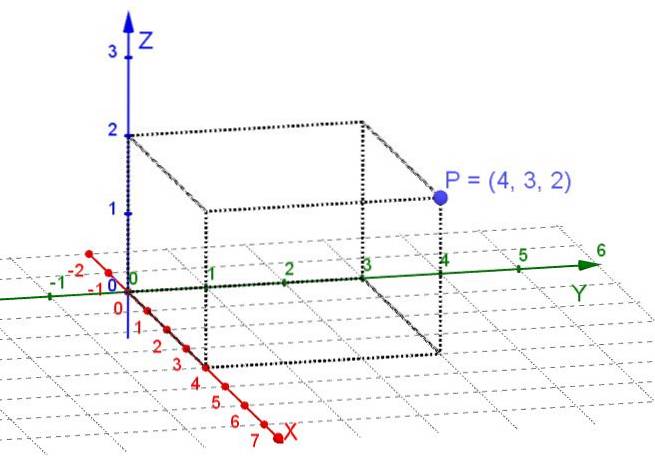
Un piano è un sottospazio dello spazio tridimensionale. Nel caso di considerare punti su un piano, allora è sufficiente scegliere una coppia di assi perpendicolari X, Y come sistema cartesiano. Quindi ad ogni punto del piano vengono assegnati due numeri reali che sono le sue coordinate rettangolari.
Indice articolo
Le coordinate rettangolari furono originariamente proposte dal matematico francese René Descartes (1596 e 1650), motivo per cui sono chiamate cartesiane.
Con questa idea di Cartesio, ai punti del piano e dello spazio vengono assegnati dei numeri, in modo che alle figure geometriche sia associata un'equazione algebrica e si possano dimostrare algebricamente i teoremi geometrici classici. Con le coordinate cartesiane nasce la geometria analitica.
Se in un piano si scelgono due rette perpendicolari che si intersecano in un punto O; e se, inoltre, a ciascuna linea è assegnata una direzione e una scala numerica tra punti equidistanti successivi, allora esiste un sistema o piano cartesiano in cui ogni punto del piano è associato a una coppia ordinata di due numeri reali che sono le loro proiezioni rispettivamente sugli assi X e Y..
I punti A = (3, 2); B = (- 2, 3); C = (- 2, -3) e D = (3, -3) sono rappresentati nel piano cartesiano come mostrato di seguito:
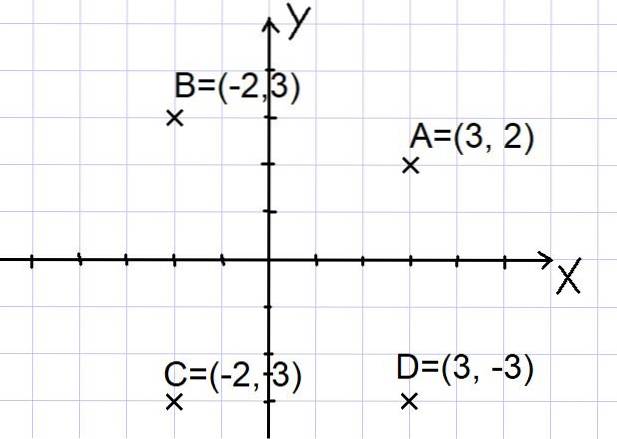
Notare che i due assi X e Y dividono il piano in quattro settori chiamati quadranti. Il punto A è nel primo quadrante, B è nel secondo quadrante, C è nel terzo quadrante e il punto D è nel quarto quadrante..
La distanza tra due punti A e B sul piano cartesiano è la lunghezza del segmento che li unisce. Questa distanza può essere calcolata analiticamente come segue:
d (A, B) = √ (Bx - Ax) ^ 2 + (By - Ay) ^ 2)
La formula sopra è ottenuta applicando il teorema di Pitagora.
Applicando questa formula ai punti A, B della figura 2 abbiamo:
d (A, B) = √ (-2 - 3) ^ 2 + (3 - 2) ^ 2) = √ (-5) ^ 2 + 1 ^ 2) = √ (26)
Cioè, d (A, B) = 5.10 unità. Si noti che la distanza è stata ottenuta senza la necessità di misurare con un righello, è stata seguita una procedura completamente algebrica.
Le coordinate rettangolari consentono la rappresentazione analitica di oggetti geometrici fondamentali come il punto e la linea. Due punti A e B definiscono un'unica linea. La pendenza della linea è definita come il quoziente tra la differenza delle coordinate Y del punto B meno A, divisa per la differenza delle coordinate X del punto B meno A:
pendenza = (By - Ay) / (Bx - Ax)
Qualsiasi punto P di coordinate (x, y) che appartiene alla linea (AB) deve avere la stessa pendenza:
pendenza = (y - Ay) / (x - Ax)
L'equazione che si ottiene mediante l'uguaglianza delle pendenze è la rappresentazione analitica o algebrica della retta che passa per i punti A e B:
(y - Ay) / (x - Ax) = (By - Ay) / (Bx - Ax).
Se prendiamo per A e B le coordinate rettangolari della figura 2 abbiamo:
(y - 2) / (x - 3) = (3 - 2) / (- 2 - 3)
(y - 2) / (x - 3) = -⅕
In questo caso particolare, abbiamo una linea con una pendenza negativa -⅕, il che significa che posizionandosi su un punto sulla linea e aumentando la coordinata x di un'unità, la coordinata y diminuisce di 0,2 unità.
Il modo più comune per scrivere l'equazione della retta nel piano è con la coordinata y deselezionata in funzione della variabile x:
y = - (1/5) x + 13/5
Ottenere con metodi analitici la distanza tra i punti C e A, essendo le coordinate rettangolari di C = (-2, -3) e quelle di A = (3,2).
La formula per la distanza euclidea tra questi due punti è scritta così:
d (A, C) = √ ((Cx - Ax) ^ 2 + (Cy - Ay) ^ 2)
Sostituendo le loro corrispondenti coordinate rettangolari abbiamo:
d (LA, DO) = √ (-2 - 3) ^ 2 + (-3 - 2) ^ 2) = √ (-5) ^ 2 + (-5) ^ 2) = 5√2 = 7,07
Ottieni l'equazione della retta che passa per il punto C delle coordinate (-2, -3) e il punto P delle coordinate (2, 0).
Innanzitutto si ottiene la pendenza della linea CP:
pendenza = (0 - (- 3)) / (2 - (-2)) = ¾
Qualsiasi punto Q di coordinate rettangolari generiche (x, y) che appartiene alla linea CP deve avere la stessa pendenza:
pendenza = (y - (- 3)) / (x - (-2)) = (y +3) / (x +2)
In altre parole, l'equazione della retta CP è:
(y +3) / (x +2) = ¾
Un modo alternativo per scrivere l'equazione della retta CP è risolvere per y:
y = ¾ x - 3/2
Ottieni le coordinate rettangolari del punto di intersezione tra le rette y = - (1/5) x + 13/5 e la retta y = ¾ x - 3/2.
Soluzione: per definizione, il punto di intersezione delle due linee condivide le stesse coordinate rettangolari. Pertanto, le coordinate y nel punto di intersezione sono identiche per entrambe le linee:
-(1/5) x + 13/5 = ¾ x - 3/2
che porta alla seguente espressione:
(¾ + ⅕) x = 13/5 +3/2
risolvendo la somma delle frazioni otteniamo:
19/20 x = 41/10
Risolvendo per x:
x = 82/19 = 4,32
Per ottenere l'intercetta y, il valore x ottenuto viene sostituito in una qualsiasi delle righe:
y = ¾ 4,32 - 3/2 = 1,74
Ciò significa che le linee date si intersecano nel punto I delle coordinate I = (4.32, 1.74).
Ottieni l'equazione della circonferenza che passa per il punto R di coordinate rettangolari (3, 4) e che ha il centro all'origine delle coordinate.
Soluzione: il raggio R è la distanza dal punto R all'origine O delle coordinate (0, 0).
d (R, O) = √ ((Rx - 0) ^ 2 + (Ry - 0) ^ 2) = √ ((3-0) ^ 2 + (4-0) ^ 2) = √ (3 ^ 2 + 4 ^ 2) = √ (9 + 16) = √ (25) = 5
Cioè, è un cerchio di raggio 5 centrato su (0,0).
Qualsiasi punto P (x, y) sulla circonferenza deve avere la stessa distanza 5 dal centro (0, 0) quindi può essere scritto:
d (P, O) = √ ((x - 0) ^ 2 + (y - 0) ^ 2) = √ (x ^ 2 + y ^ 2) = 5
Vale a dire:
√ (x ^ 2 + y ^ 2) = 5
Per eliminare la radice quadrata, entrambi i membri dell'uguaglianza vengono al quadrato, ottenendo:
x ^ 2 + y ^ 2 = 25
Qual è l'equazione della circonferenza.
Questo esempio illustra la potenza del sistema di coordinate rettangolari, che consente di determinare oggetti geometrici, come la circonferenza, senza la necessità di utilizzare carta, matita e compasso. La circonferenza richiesta è stata determinata esclusivamente con metodi algebrici.
Nessun utente ha ancora commentato questo articolo.