
Arresti anelastici in una dimensione ed esempi
Il shock anelastici o le collisioni anelastiche sono una breve e intensa interazione tra due oggetti in cui viene conservata la quantità di moto, ma non l'energia cinetica, di cui una percentuale si trasforma in qualche altro tipo di energia.
Gli incidenti o le collisioni sono frequenti in natura. Le particelle subatomiche si scontrano a velocità estremamente elevate, mentre molti sport e giochi sono costituiti da collisioni continue. Anche le galassie sono in grado di scontrarsi.

In realtà, la quantità di moto è conservata in qualsiasi tipo di collisione, purché le particelle in collisione formino un sistema isolato. Quindi in questo senso non c'è problema. Ora, gli oggetti hanno energia cinetica associata al movimento che hanno. Cosa può accadere a quell'energia in caso di collisione??
Le forze interne che si verificano durante la collisione tra oggetti sono forti. Quando si afferma che l'energia cinetica non è conservata, significa che si trasforma in altri tipi di energia: ad esempio, in energia sonora (una collisione spettacolare ha un suono distintivo).
Maggiori possibilità di utilizzo dell'energia cinetica: il calore per attrito, e ovviamente l'inevitabile deformazione che subiscono gli oggetti in collisione, come le scocche delle auto nella figura sopra.
Indice articolo
- 1 Esempi di collisioni anelastiche
- 2 Collisioni perfettamente anelastiche in una dimensione
- 3 Coefficiente di restituzione
- 4 Come determinare il coefficiente di restituzione?
- 5 esempi lavorati
- 5.1 -Esercizio 1
- 5.2 -Esercizio 2
- 5.3 -Esercizio 3
- 6 Riferimenti
Esempi di collisioni anelastiche
- Due masse di plastilina che si scontrano e si attaccano, muovendosi come un unico pezzo dopo la collisione.
- Una palla di gomma che rimbalza su un muro o un pavimento. La palla si deforma quando colpisce la superficie.
Non tutta l'energia cinetica si trasforma in altri tipi di energia, con poche eccezioni. Gli oggetti possono trattenere una certa quantità di questa energia. Successivamente vedremo come calcolare la percentuale.
Quando i pezzi in collisione si uniscono, la collisione viene definita perfettamente anelastica ed entrambi tendono a muoversi insieme..
Collisioni perfettamente anelastiche in una dimensione
La collisione nella figura mostra due oggetti di massa diversa m1 Y mDue, muovendosi l'uno verso l'altro con velocità vi1 Y vi2 rispettivamente. Tutto accade in orizzontale, cioè è una collisione in una dimensione, la più facile da studiare.
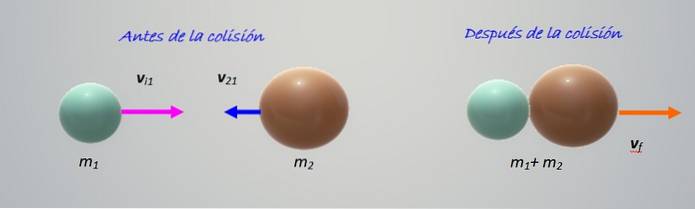
Gli oggetti entrano in collisione e poi si uniscono spostandosi verso destra. È una collisione perfettamente anelastica, quindi dobbiamo solo mantenere lo slancio:
Po = PF
Il momento è un vettore le cui unità SI sono N.s. Nella situazione descritta, si può fare a meno della notazione vettoriale quando si tratta di collisioni in una dimensione:
mvo = mvF
La quantità di moto del sistema è la somma vettoriale della quantità di moto di ciascuna particella.
m1 vi1 + mDue vi2 = (m1 + mDue) vF
La velocità finale è data da:
vF = (m1 vi1 + mDue vi2) / (m1 + mDue)
Coefficiente di restituzione
C'è una quantità che può indicare quanto sia elastica una collisione. Riguarda coefficiente di restituzione, che è definito come il quoziente negativo tra la velocità relativa delle particelle dopo la collisione e la velocità relativa prima della collisione.
Let u1 e tuDue inizialmente le rispettive velocità delle particelle. Ed essere v1 e VDue le rispettive velocità finali. Matematicamente il coefficiente di restituzione può essere espresso come segue:
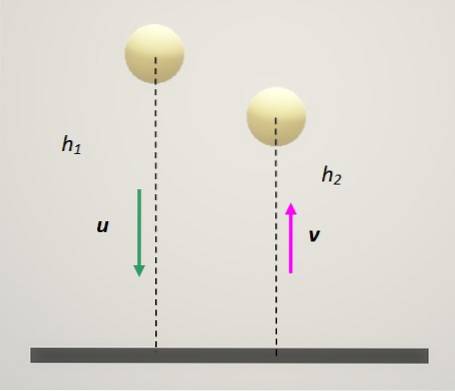
- Se ε = 0 equivale ad affermare che vDue = v1. Significa che le velocità finali sono le stesse e l'urto è anelastico, come quello descritto nella sezione precedente..
- Quando ε = 1 significa che le velocità relative sia prima che dopo l'urto non cambiano, in questo caso l'urto è elastico.
- E se 0 < ε < 1 parte de la energía cinética de la colisión se transforma en alguna otra de las energías mencionadas anteriormente.
Come determinare il coefficiente di restituzione?
Il coefficiente di restituzione dipende dalla classe dei materiali coinvolti nell'urto. Un test molto interessante per determinare quanto sia elastico un materiale per fare palline è far cadere la pallina su una superficie fissa e misurare l'altezza di rimbalzo.

In questo caso, il piatto fisso ha sempre velocità 0. Se gli viene assegnato l'indice 1 e l'indice palla 2 è:
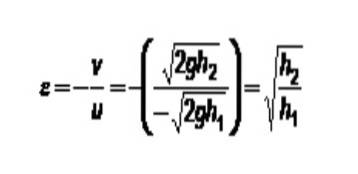



All'inizio è stato suggerito che tutta l'energia cinetica può essere trasformata in altri tipi di energia. Dopotutto, l'energia non viene distrutta. È possibile che oggetti in movimento si scontrino e si uniscano per formare un unico oggetto che improvvisamente si ferma? Non è così facile da immaginare.
Tuttavia, immaginiamo che avvenga il contrario, come in un film visto al contrario. Quindi l'oggetto era inizialmente a riposo e poi esplode, frammentandosi in varie parti. Questa situazione è perfettamente possibile: è un'esplosione.
Quindi un'esplosione può essere pensata come una collisione perfettamente anelastica vista indietro nel tempo. Anche lo slancio è conservato e si può affermare che:
Po = PF
Esempi lavorati
-Esercizio 1
È noto dalle misurazioni che il coefficiente di restituzione dell'acciaio è 0,90. Una sfera d'acciaio viene fatta cadere da un'altezza di 7 m su una piastra fissa. Calcolare:
a) Quanto in alto rimbalzerà.
b) Quanto tempo ci vuole tra il primo contatto con la superficie e il secondo.
Soluzione
a) Si utilizza l'equazione dedotta in precedenza nella sezione relativa alla determinazione del coefficiente di restituzione:
L'altezza viene cancellata hDue:
0.90Due . 7 m = 5,67 m
b) Per salire di 5,67 metri, è richiesta una velocità data da:


t max = vo/ g = (10,54 / 9,8 s) = 1,08 s.
Il tempo necessario per il rientro è lo stesso, quindi il tempo totale per salire i 5,67 metri e tornare al punto di partenza è il doppio del tempo massimo:
tvolo = 2,15 s.
-Esercizio 2
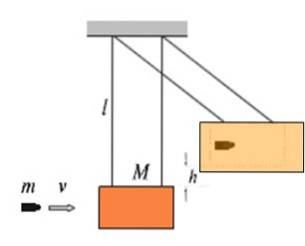
La figura mostra un blocco di legno di massa M appeso a riposo con corde di lunghezza l come un pendolo. Questo è chiamato pendolo balistico e viene utilizzato per misurare la velocità v di ingresso in un proiettile di massa m. Maggiore è la velocità con cui il proiettile colpisce il blocco, maggiore sarà l'altezza.
Il proiettile nell'immagine è incorporato nel blocco, quindi è uno shock totalmente anelastico.

Supponiamo che un proiettile da 9,72 g colpisca il blocco di massa di 4,60 kg, quindi l'assemblaggio si alza di 16,8 cm dall'equilibrio. Qual è la velocità v dal proiettile?
Soluzione
Durante la collisione lo slancio è conservato e oF è la velocità del tutto, una volta che il proiettile si è incorporato nel blocco:
Po = PF
Il blocco è inizialmente fermo, mentre il proiettile è mirato al bersaglio con velocità v:
m.v + M.0 = (m + M) uF
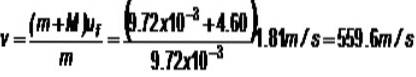
Non conosciuto oF ancora, ma dopo l'urto si conserva l'energia meccanica, essendo questa la somma dell'energia potenziale gravitazionale U e dell'energia cinetica K:
Energia meccanica iniziale = Energia meccanica finale
Emo = Emf
Oo + Ko = UF + KF
L'energia potenziale gravitazionale dipende dall'altezza a cui raggiunge l'insieme. Per la posizione di equilibrio l'altezza iniziale è quella presa come livello di riferimento, quindi:
Oo = 0
Grazie al proiettile, il tutto ha energia cinetica Ko, che viene convertita in energia potenziale gravitazionale quando l'insieme raggiunge la sua altezza massima h. L'energia cinetica è data da:
K = ½ mvDue
Inizialmente l'energia cinetica è:
Ko = (1/2) (M + m) uFDue
Ricorda che il proiettile e il blocco formano già un unico oggetto di massa M + m. L'energia potenziale gravitazionale quando hanno raggiunto la loro altezza massima è:
OF = (m + M) gh
Perciò:
Ko = UF
(1/2) (M + m) uFDue = (m + M) gh
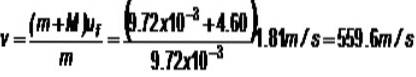
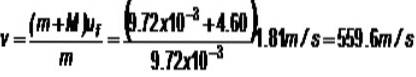
-Esercizio 3
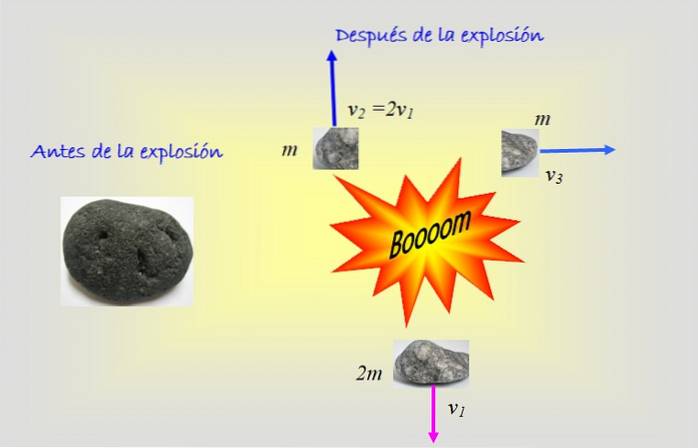
L'oggetto nella figura esplode in tre frammenti: due di massa uguale me uno più grande di massa 2m. La figura mostra le velocità di ogni frammento dopo l'esplosione. Qual era la velocità iniziale dell'oggetto?
Soluzione
In questo problema è richiesto l'uso di due coordinate: X e Y, perché due dei frammenti hanno velocità verticali, mentre il resto ha velocità orizzontale.
La massa totale dell'oggetto è la somma della massa di tutti i frammenti:
M = m + m + 2m = 4m
La quantità di moto è conservata sia sull'asse x che sull'asse y, è dichiarato separatamente:
- 4m. oX= m v3
- 4m. oY = m. 2v1 - 2m. v1
Si noti che il frammento grande si sposta verso il basso con velocità v1, per indicare questo fatto è stato posizionato un segno negativo su di esso.
Dalla seconda equazione ne consegue immediatamente che oY = 0, e dal primo, ux viene immediatamente cancellato:

Riferimenti
- Giancoli, D. 2006. Fisica: principi con applicazioni. 6th. Ed Prentice Hall. 175-181
- Rex, A. 2011. Fondamenti di fisica. Pearson. 135-155.
- Serway, R., Vulle, C. 2011. Fondamenti di fisica. 9n / A Cengage Learning. 172-182
- Tipler, P. (2006) Physics for Science and Technology. 5a Ed. Volume 1. Editoriale Reverté. 217-238
- Tippens, P. 2011. Fisica: concetti e applicazioni. 7a edizione. MacGraw Hill. 185-195

Nessun utente ha ancora commentato questo articolo.