
Distribuzione chi-quadrato (χ²), come calcolarla, esempi
La prova Chi al quadrato o chi-quadrato (χDue, dove χ è la lettera greca chiamata "chi") è usato per determinare il comportamento di una certa variabile e anche quando vuoi sapere se due o più variabili sono statisticamente indipendenti.
Per verificare il comportamento di una variabile viene chiamato il test da eseguire test di adattamento chi quadrato. Per scoprire se due o più variabili sono statisticamente indipendenti, viene chiamato il test chi quadrato dell'indipendenza, chiamato anche contingenza.
Questi test fanno parte della teoria delle decisioni statistiche, in cui si studia una popolazione e si prendono decisioni al riguardo, analizzando uno o più campioni presi da essa. Ciò richiede di fare alcune ipotesi sulle variabili, chiamate ipotesi, che può o non può essere vero.
Esistono alcuni test per contrastare queste congetture e determinare quali sono valide, entro un certo margine di confidenza, incluso il test del chi-quadrato, che può essere applicato per confrontare due e più popolazioni..
Come vedremo, due tipi di ipotesi vengono solitamente sollevate su alcuni parametri della popolazione in due campioni: l'ipotesi nulla, chiamata Ho (i campioni sono indipendenti) e l'ipotesi alternativa, indicata come H.1, (i campioni sono correlati) che è l'opposto di quello.
Indice articolo
- 1 Quando viene utilizzato il test chi quadrato?
- 1.1 Condizioni per applicarlo
- 2 distribuzione Chi quadrato
- 2.1 Gradi di libertà
- 2.2 Formulazione di ipotesi
- 3 Come viene calcolata la statistica del chi quadrato?
- 3.1 Criteri di accettazione per Ho
- 4 Esempio di calcolo
- 5 Riferimenti
Quando viene utilizzato il test chi quadrato?
Il test del chi quadrato viene applicato a variabili che descrivono qualità, come sesso, stato civile, gruppo sanguigno, colore degli occhi e preferenze di vario tipo.
Il test è inteso quando vuoi:
-Verificare se una distribuzione è appropriata per descrivere una variabile, che viene chiamata bontà di adattamento. Utilizzando il test chi-quadrato, è possibile sapere se ci sono differenze significative tra la distribuzione teorica selezionata e la distribuzione di frequenza osservata..
-Scopri se due variabili X e Y sono indipendenti dal punto di vista statistico. Questo è noto come test di indipendenza.
Poiché viene applicato a variabili qualitative o categoriali, il test chi-quadrato è ampiamente utilizzato nelle scienze sociali, nella gestione e nella medicina..
Condizioni per applicarlo
Ci sono due requisiti importanti per applicarlo correttamente:
-I dati devono essere raggruppati in frequenze.
-Il campione deve essere sufficientemente grande perché la distribuzione del chi quadrato sia valida, altrimenti il suo valore viene sovrastimato e porta al rifiuto dell'ipotesi nulla quando non dovrebbe essere il caso..
La regola generale è che se nei dati raggruppati compare una frequenza con un valore inferiore a 5, non viene utilizzata. Se è presente più di una frequenza inferiore a 5, è necessario combinarle in una sola per ottenere una frequenza con un valore numerico maggiore di 5.
Distribuzione del Chi quadrato
χDue è una distribuzione continua di probabilità. In realtà ci sono curve diverse, a seconda di un parametro K chiamato gradi di libertà della variabile casuale.
Le sue proprietà sono:
-L'area sotto la curva è uguale a 1.
-I valori di χDue sono positivi.
-La distribuzione è asimmetrica, cioè ha un bias.
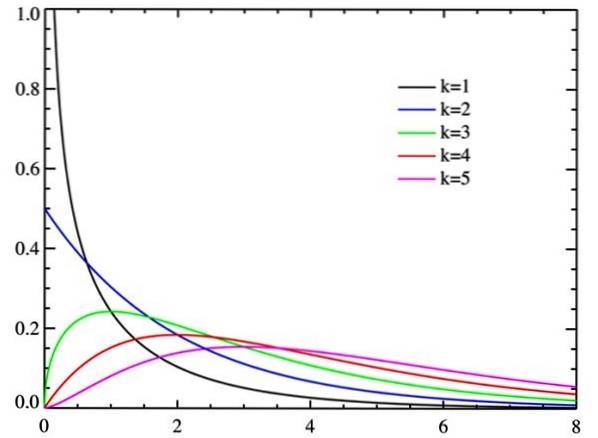
Gradi di libertà
All'aumentare dei gradi di libertà, la distribuzione del chi quadrato tende alla normalità, come si può vedere dalla figura.
Per una data distribuzione, i gradi di libertà sono determinati tramite tabella di contingenza, che è la tabella in cui vengono registrate le frequenze osservate delle variabili.
Se un tavolo ha F righe e c colonne, il valore di K è:
k = (f - 1) ⋅ (c - 1)
Formulazione di ipotesi
Quando il test del chi quadrato è di adattamento, vengono formulate le seguenti ipotesi:
-Ho: la variabile X ha una distribuzione di probabilità f (x) con i parametri specifici y1, YDue..., Yp
-H1: X ha un'altra distribuzione di probabilità.
La distribuzione di probabilità assunta nell'ipotesi nulla può essere, ad esempio, la distribuzione normale nota, ei parametri sarebbero la media μ e la deviazione standard σ.
Inoltre, l'ipotesi nulla viene valutata con un certo livello di significatività, cioè una misura dell'errore che verrebbe commesso rifiutando che fosse vera.
Di solito questo livello è impostato su 1%, 5% o 10% e più è basso, più affidabile è il risultato del test..
E se si utilizza il test chi-quadrato della contingenza, che, come abbiamo detto, serve a verificare l'indipendenza tra due variabili X e Y, le ipotesi sono:
-Ho: le variabili X e Y sono indipendenti.
-H1: X e Y sono dipendenti.
Ancora una volta, è necessario specificare un livello di significatività per conoscere la misura dell'errore quando si prende la decisione..
Come viene calcolata la statistica del chi quadrato?
La statistica del chi quadrato viene calcolata come segue:

La somma viene eseguita dalla prima classe i = 1 all'ultima, che è i = k.
Cosa c'è di più:
-Fo è una frequenza osservata (proviene dai dati ottenuti).
-Fe è la frequenza prevista o teorica (deve essere calcolata dai dati).
Per accettare o rifiutare l'ipotesi nulla, calcoliamo χDue per i dati osservati e confrontati con un valore chiamato chi quadrato critico, che dipende dai gradi di libertà K e il livello di significatività α:
χDuecritico = χDuek, α
Se, ad esempio, vogliamo eseguire il test con un livello di significatività dell'1%, allora α = 0,01, se sarà del 5% allora α = 0,05 e così via. Definiamo p, il parametro della distribuzione, come:
p = 1 - α
Questi valori critici del chi quadrato sono determinati da tabelle contenenti il valore dell'area cumulativa. Ad esempio, per k = 1, che rappresenta 1 grado di libertà e α = 0,05, che è uguale a p = 1- 0,05 = 0,95, il valore di χDue è 3.841.

Criteri di accettazione H.o
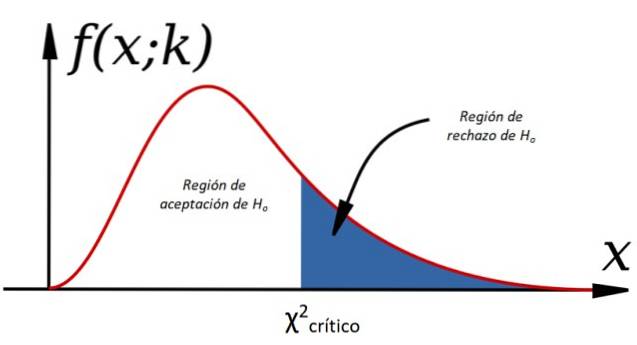
Il criterio per accettare Ho è:
-Sì χDue < χDuecritico H è accettatoo, altrimenti viene rifiutato (vedi figura 1).
Esempio di calcolo
Nella seguente applicazione il test chi quadrato sarà utilizzato come test di indipendenza.
Supponiamo che i ricercatori vogliano sapere se la preferenza per il caffè nero è correlata al sesso della persona e specificano la risposta con un livello di significatività α = 0,05.
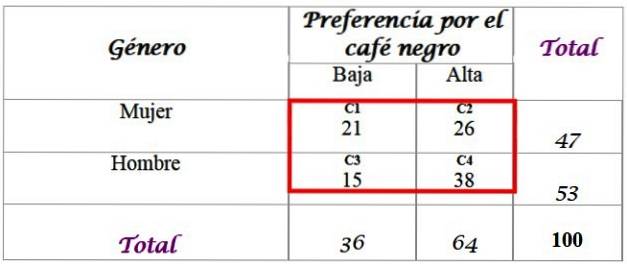
Per questo, è disponibile un campione di 100 persone intervistate e le loro risposte:
Passo 1
Stabilisci le ipotesi:
-Ho: il genere e la preferenza per il caffè nero sono indipendenti.
-H1: il gusto per il caffè nero è legato al sesso della persona.
Passo 2
Calcola le frequenze previste per la distribuzione, per le quali sono richiesti i totali aggiunti nell'ultima riga e nella colonna di destra della tabella. Ogni cella nella casella rossa ha un valore previsto Fe, che viene calcolato moltiplicando il totale della riga F per il totale della colonna C, diviso per il totale del campione N:
Fe = (F x C) / N
I risultati sono i seguenti per ogni cella:
-C1: (36 x 47) / 100 = 16,92
-C2: (64 x 47) / 100 = 30,08
-C3: (36 x 53) / 100 = 19,08
-C4: (64 x 53) / 100 = 33,92
Passaggio 3
Successivamente, la statistica chi-quadrato deve essere calcolata per questa distribuzione, secondo la formula data:

Passaggio 4
Determina χDuecritico, sapendo che i dati registrati sono in f = 2 righe ec = 2 colonne, quindi, il numero di gradi di libertà è:
k = (2-1) ⋅ (2-1) = 1.
Ciò significa che dobbiamo cercare nella tabella mostrata sopra il valore di χDuek, α = χDue1; 0,05 , che è:
χDuecritico = 3.841
Passaggio 5
Confronta i valori e decidi:
χDue = 2.9005
χDuecritico = 3.841
Dal momento che χDue < χDuecritico si accetta l'ipotesi nulla e si conclude che la preferenza per il caffè nero non è legata al genere della persona, con un livello di significatività del 5%.
Riferimenti
- Test del chi quadrato per l'indipendenza. Recupero da: saylordotorg.github.io.
- Med Wave. Statistica applicata alle scienze della salute: il test chi-quadrato. Estratto da: medwave.cl.
- Probabilità e statistica. Test di bontà di adattamento chi quadrato. Estratto da: probayestadistica.com.
- Triola, M. 2012. Statistica elementare. 11 °. Edizione. Addison Wesley.
- UNAM. Test del chi quadrato. Recupero da: asesorias.cuautitlan2.unam.mx.



Nessun utente ha ancora commentato questo articolo.