
Concetti, metodi, esempi di analisi delle mesh
Il analisi della maglia è una tecnica utilizzata per risolvere circuiti elettrici piatti. Questa procedura può anche apparire in letteratura con i nomi dei metodi di correnti di circuito o metodo di correnti di maglia (o loop).
Il fondamento di questo e di altri metodi di analisi dei circuiti elettrici è nelle leggi di Kirchhoff e nella legge di Ohm. Le leggi di Kirchhoff, a loro volta, sono espressioni di due principi di conservazione molto importanti in Fisica per sistemi isolati: sia la carica elettrica che l'energia sono conservate..

Da un lato, la carica elettrica è correlata alla corrente, che è la carica in movimento, mentre in un circuito l'energia è legata alla tensione, che è l'agente incaricato di fare il lavoro necessario per mantenere la carica in movimento..
Queste leggi, applicate a un circuito piatto, generano un insieme di equazioni simultanee che devono essere risolte per ottenere i valori di corrente o tensione..
Il sistema di equazioni può essere risolto con tecniche analitiche familiari, come regola di cramer, ciò richiede il calcolo delle determinanti per ottenere la soluzione del sistema.
A seconda del numero di equazioni, vengono risolte utilizzando una calcolatrice scientifica o un software matematico. In rete ci sono anche molte opzioni disponibili.
Indice articolo
- 1 Termini importanti
- 2 metodi
- 2.1 - Passaggi per applicare l'analisi della mesh
- 3 esercizi risolti
- 3.1 - Esempio 1
- 3.2 - Esempio 2
- 4 Riferimenti
Termini importanti
Prima di spiegare come funziona, inizieremo definendo questi termini:
Ramo: sezione contenente un elemento del circuito.
Nodo: punto che collega due o più rami.
Nastro: è una qualsiasi porzione chiusa di un circuito, che inizia e finisce nello stesso nodo.
Maglia: ciclo che non contiene nessun altro ciclo all'interno (maglia essenziale).
Metodi
L'analisi della mesh è un metodo generale utilizzato per risolvere circuiti i cui elementi sono collegati in serie, in parallelo o in modo misto, cioè quando il tipo di connessione non è chiaramente distinto. Il circuito deve essere piatto, o almeno deve essere possibile ridisegnarlo come tale.
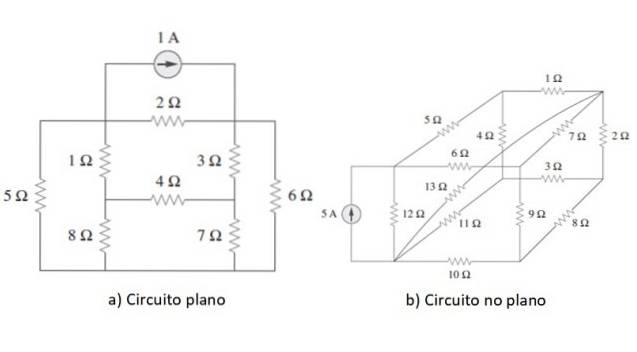
Un esempio di ogni tipo di circuito è mostrato nella figura sopra. Una volta chiarito il punto, per iniziare, applicheremo il metodo ad un semplice circuito come esempio nella prossima sezione, ma prima passeremo in rassegna brevemente le leggi di Ohm e Kirchhoff.
Legge di Ohm: essere V la tensione, R resistenza e io la corrente dell'elemento resistivo ohmico, in cui la tensione e la corrente sono direttamente proporzionali, essendo la resistenza la costante di proporzionalità:
V = I.R
Legge della tensione di Kirchhoff (LKV): In ogni percorso chiuso percorso in una sola direzione, la somma algebrica delle tensioni è zero. Ciò include le tensioni dovute a sorgenti, resistori, induttori o condensatori: ∑ E = ∑ Rio. io
Legge della corrente di Kirchhoff (LKC): in ogni nodo, la somma algebrica delle correnti è zero, tenendo conto che alle correnti entranti è assegnato un segno e quelle uscenti un altro. In questo modo: ∑ I = 0.
Con il metodo della corrente mesh, non è necessario applicare l'attuale legge di Kirchhoff, con il risultato di un minor numero di equazioni da risolvere.
- Passaggi per applicare l'analisi della mesh
Inizieremo spiegando il metodo per un circuito a 2 mesh. La procedura può quindi essere estesa per circuiti più grandi.
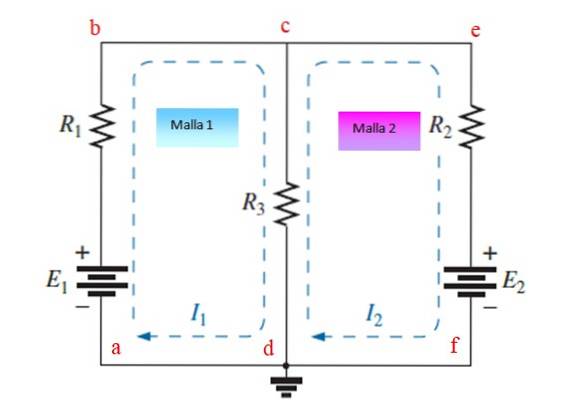
Passo 1
Assegna e disegna correnti indipendenti a ciascuna mesh, in questo esempio lo sono io1 e ioDue. Possono essere disegnati in senso orario o antiorario.
Passo 2
Applicare la legge delle tensioni di Kirchhoff (LTK) e la legge di Ohm a ciascuna mesh. Alle potenziali cadute viene assegnato un segno (-) mentre alle alzate viene assegnato un segno (+).
Mesh abcda
Partendo dal punto a e seguendo la direzione della corrente, troviamo un potenziale aumento della batteria E1 (+), quindi un calo di R1 (-) e poi un altro calo di R3 (-).
Contemporaneamente, la resistenza R3 è attraversato anche dalla corrente IDue, ma nella direzione opposta, quindi rappresenta un aumento (+). La prima equazione ha questo aspetto:
E1-R1.io1 -R3.io1 + R3.ioDue = 0
Quindi viene scomposto e i termini vengono raggruppati:
- (R1+R3) IO1 +R3ioDue = -E1 (Equazione 1)
Cefdc mesh
A partire dal punto e e seguendo la direzione della corrente, si riscontra un potenziale calo RDue (-), un altro calo EDue, poiché la corrente entra attraverso il polo + della batteria e infine un altro calo R3 (-), Allo stesso tempo, la corrente io1 attraversa R3 nella direzione opposta (+).
La seconda equazione, con i segni indicati, si presenta così:
- RDue ioDue - EDue -R3 ioDue +R3 io1= 0
R3io1 - (RDue +R3) ioDue = EDue (Equazione 2)
Nota che ci sono due equazioni con le due incognite I1 e ioDue.
Passaggio 3
Il sistema di equazioni così formato viene quindi risolto.
Esercizi risolti
Per iniziare, è importante considerare quanto segue:
-Alle correnti di loop o alle correnti di maglia può essere assegnato un indirizzo arbitrario.
-Ad ogni maglia essenziale - o "finestra" - che il circuito possiede deve essere assegnata una corrente.
-Le correnti della maglia sono indicate con una lettera maiuscola per distinguerle dalle correnti che circolano attraverso i rami, sebbene in alcuni casi la corrente che circola attraverso un ramo può essere la stessa di quella della maglia.
- Esempio 1
Trova le correnti che fluiscono attraverso ciascun resistore nel circuito della figura 3, se gli elementi hanno i seguenti valori:
R1 = 20 Ω; RDue = 30 Ω; R3 = 10 Ω; E1 = 12 V; EDue = 18 V
Soluzione
Innanzitutto, è necessario assegnare le correnti di maglia I.1 e ioDue e prendi il sistema di equazioni come dedotto nella sezione precedente, quindi sostituisci i valori forniti nell'istruzione:
- (R1+R3) IO1 +R3ioDue = -E1 (Equazione 1)
R3io1 - (RDue +R3) ioDue = EDue (Equazione 2)
-
-(20 + 30) io1 + 10IDue = -12
10I1 - (30 +10) IDue = 18
--
-cinquantaio1 + 10IDue = -12
10I1 - 40 I.Due = 18
Poiché è un sistema di equazioni 2 x 2, può essere facilmente risolto per riduzione, moltiplicando la seconda equazione per 5 per eliminare l'ignoto io1:
-cinquantaio1 + 10 IDue = -12
50I1 - 200 IDue = 90
-
-190 IDue= 78
ioDue = - 78/180 A = - 0,41 A
Immediatamente la corrente si schiarisce io1 da una qualsiasi delle equazioni originali:
io1 = (18 + 40 IDue) / 10 = (18 + 40 x (-0,41)) / 10 = 0,16 A
Il segno negativo nella corrente ioDue significa che la corrente nella maglia 2 circola in direzione opposta a quella tracciata.
Le correnti in ogni resistenza sono le seguenti:
Per la resistenza R1 la corrente circola io1 = 0,16 A nel senso attirato, dalla resistenza RDue la corrente circola ioDue = 0,41 A nella direzione opposta a quella disegnata e dalla resistenza R3 circolare io3 = 0,16- (-0,41) A = 0,57 A giù.
Soluzione di sistema con il metodo di Cramer
In forma di matrice, il sistema può essere risolto come segue:
Passaggio 1: calcolare Δ

Passaggio 2: calcolare Δ1
La prima colonna è sostituita dai termini indipendenti del sistema di equazioni, mantenendo l'ordine in cui il sistema è stato originariamente proposto:

Passaggio 3: calcola I.1
io1 = Δ1/ Δ = 300/1900 = 0,16 A
Passaggio 4: calcolare ΔDue

ioDue = ΔDue/ Δ = -780/1900 = -0,41 A
- Esempio 2
Determina la corrente e le tensioni attraverso ciascun resistore nel seguente circuito, utilizzando il metodo delle correnti di rete:

Soluzione
Le tre correnti di maglia vengono tracciate, come mostrato nella figura seguente, in direzioni arbitrarie. Ora le mesh vengono attraversate partendo da un punto qualsiasi:
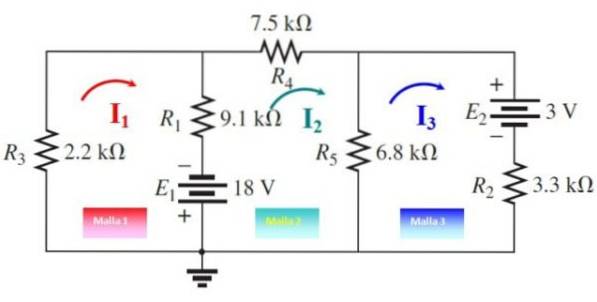
Maglia 1
-9100.I1+18-2200.I1+9100.IDue= 0
-11300 I1 + 9100.IDue = -18
Maglia 2
-(7500 + 6800 + 9100) I.Due + 9100.I1+6800.I3-18 = 0
9100.I1 - 23400.IDue + 6800.I3 = 18
Maglia 3
-(6800 + 3300) I.3 + 6800.IDue - 3 = 0
6800.IDue - 10100.I3 = 3
Sistema di equazioni
-11300 I1 + 9100.IDue + 0.I3= -18
9100.I1 - 23400.IDue + 6800.I3 = 18
0.I1 + 6800.IDue - 10100.I3 = 3
Sebbene i numeri siano grandi, può essere risolto rapidamente con l'aiuto di una calcolatrice scientifica. Ricorda che le equazioni devono essere ordinate e aggiungi zeri nei punti in cui l'ignoto non appare, come appare qui.
Le correnti di maglia sono:
io1 = 0,0012 A; ioDue = -0,00048 A; io3 = -0,00062 A
Correnti ioDue e io3 circolano in direzione opposta a quella mostrata in figura, poiché si sono rivelati negativi.
Tabella delle correnti e delle tensioni in ciascuna resistenza
| Resistenza (Ω) | Corrente (Amp) | Tensione = I.R (Volt) |
|---|---|---|
| 9100 | io1 -ioDue = 0,0012 - (- 0,00048) = 0,00168 | 15.3 |
| 3300 | 0.00062 | 2.05 |
| 2200 | 0.0012 | 2.64 |
| 7500 | 0.00048 | 3.60 |
| 6800 | ioDue -io3= -0.00048 - (- 0.00062) = 0.00014 | 0.95 |
La soluzione della regola di Cramer
Poiché sono numeri grandi, è conveniente utilizzare la notazione scientifica per lavorare direttamente con loro.
Calcolo di I.1
Le frecce colorate nel determinante 3 x 3 indicano come trovare i valori numerici moltiplicando i valori indicati. Cominciamo ottenendo quelli della prima parentesi nel determinante Δ:
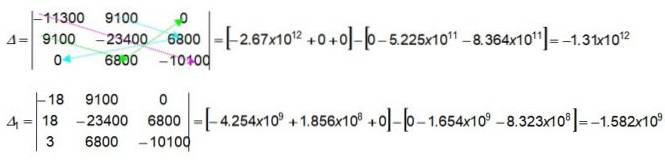
(-11300) x (-23400) x (-10100) = -2,67 x 1012
9100 x 0 x 0 = 0
9100 x 6800 x 0 = 0
Immediatamente otteniamo la seconda parentesi nello stesso determinante, che viene lavorata da sinistra verso destra (per questa parentesi le frecce colorate non sono state disegnate nella figura). Invitiamo il lettore a verificarlo:
0 x (-23400) x 0 = 0
9100 x 9100 x (-10100) = -8,364 x 10undici
6800 x 6800 x (-11300) = -5,225 x 10undici
Allo stesso modo, il lettore può anche controllare i valori per il determinante Δ1.
Importante: tra entrambe le parentesi c'è sempre un segno negativo.
Finalmente ottieni la corrente io1 attraverso io1 = Δ1 / Δ
io1 = -1,582 x 109/-1,31 x 1012 = 0,0012 A
Calcolo di I.Due
La procedura può essere ripetuta per calcolare ioDue, in questo caso, calcolare il determinante ΔDue la seconda colonna del determinante Δ viene sostituita dalla colonna dei termini indipendenti e si trova il suo valore, secondo la procedura spiegata.
Tuttavia, poiché è ingombrante a causa dei grandi numeri, soprattutto se non si dispone di una calcolatrice scientifica, la cosa più semplice è sostituire il valore di io1 già calcolato, nella seguente equazione e chiaro:
-11300 I1 + 9100.IDue + 0.I3= -18 → 9100 IDue= -18 + 11300 I1 → IoDue = -0,00048 A
Calcolo di I3
Una volta con i valori di io1 e ioDue in mano, quello di io3 trovato direttamente per sostituzione.
Riferimenti
- Alexander, C. 2006. Fondamenti di circuiti elettrici. 3 °. Edizione. Mc Graw Hill.
- Boylestad, R. 2011. Introduzione alla Circuit Analysis.2da. Edizione. Pearson.
- Figueroa, D. (2005). Serie: Fisica per la scienza e l'ingegneria. Volume 5. Interazione elettrica. A cura di Douglas Figueroa (USB).
- García, L. 2014. Elettromagnetismo. 2 °. Edizione. Università industriale di Santander.
- Sears, Zemansky. 2016. Fisica universitaria con fisica moderna. 14th. Ed. Volume 2.



Nessun utente ha ancora commentato questo articolo.