
Definizione, condizioni, esercizi di vettori non complanari
Il vettori non complanari sono quelli che non condividono lo stesso aereo. Due vettori liberi e un punto definiscono un unico piano. Un terzo vettore può condividere o meno quel piano e, se non lo fa, sono vettori non complanari.
I vettori non complanari non possono essere rappresentati in spazi bidimensionali come una lavagna o un foglio di carta, perché alcuni di essi sono contenuti nella terza dimensione. Per rappresentarli correttamente devi usare la prospettiva.
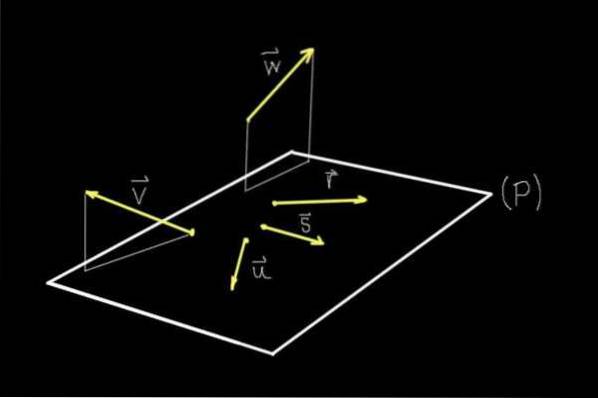
Se guardiamo la figura 1, tutti gli oggetti mostrati sono rigorosamente nel piano dello schermo, tuttavia grazie alla prospettiva il nostro cervello è in grado di immaginare un piano (P) che ne esce..
Su quel piano (P) ci sono i vettori r, S, o, mentre i vettori v Y w non sono su quell'aereo.
Quindi i vettori r, S, o sono complanari o complanari tra loro poiché condividono lo stesso piano (P). Vettori v Y w non condividono un piano con nessuno degli altri vettori mostrati, quindi non sono complanari.
Indice articolo
- 1 Vettori complanari ed equazione del piano
- 1.1 Equazione cartesiana del piano
- 2 Condizioni affinché tre vettori non siano complanari
- 2.1 Condizione di non complanarità
- 2.2 Condizione alternativa di non complanarità
- 3 esercizi risolti
- 3.1 -Esercizio 1
- 3.2 -Esercizio 2
- 4 Riferimenti
Vettori complanari ed equazione del piano
Un piano è definito in modo univoco se tre punti si verificano nello spazio tridimensionale.
Supponiamo che questi tre punti siano il punto PER, punto B e il punto C che definiscono l'aereo (P). Con questi punti è possibile costruire due vettori AB = u Y AC = v che sono per costruzione complanari al piano (P).
Il prodotto vettoriale (o prodotto incrociato) di questi due vettori risulta in un terzo vettore perpendicolare (o normale) ad essi e quindi perpendicolare al piano (P):
n = u X v => n ⊥ o Y n ⊥ v => n ⊥ (P)
Qualsiasi altro punto che appartiene all'aereo (P) deve soddisfare che il vettore AQ è perpendicolare al vettore n; Ciò equivale a dire che il prodotto scalare (o prodotto scalare) di n con AQ deve essere zero:
n • AQ = 0 (*)
La condizione precedente equivale a dire che:
AQ • (o X v) = 0
Questa equazione garantisce che il punto Q appartengono all'aereo (P).
Equazione cartesiana del piano
L'equazione di cui sopra può essere scritta in forma cartesiana. Per questo scriviamo le coordinate dei punti PER, Q e le componenti del vettore normale n:
A = (a, b, c)
Q = (x, y, z)
n= (nx, ny, nz)
Quindi i componenti di AQ sono:
AQ= (x-a, y-b, z-c)
La condizione per il vettore AQ è contenuto nell'aereo (P) è la condizione (*) che ora si scrive così:
(nx, ny, nz) • (x-a, y-b, z-c) = 0
Il calcolo del prodotto scalare rimane:
nx (x-a) + ny (y-b) + nz (z-b) = 0
Se viene sviluppato e riorganizzato rimane:
nx x + ny y + nz z = nx a + ny b + nz c
L'espressione precedente è l'equazione cartesiana di un piano (P), in funzione delle componenti di un vettore normale a (P) e le coordinate di un punto PER che appartiene a (P).
Condizioni per tre vettori non complanari
Come visto nella sezione precedente, la condizione AQ • (o X v) = 0 garantisce che il vettore AQ è complanare a o Y v.
Se chiamiamo w vettore AQ allora possiamo affermare che:
w, o Y v sono complanari, se e solo se w • ( o X v ) = 0.
Condizione di non complanarità
Se il triplo prodotto (o prodotto misto) di tre vettori è diverso da zero, questi tre vettori non sono complanari.
sì w • ( o X v ) ≠ 0 allora i vettori u, v e w sono non complanari.
Se vengono introdotte le componenti cartesiane dei vettori u, v e w, la condizione di non complanarità può essere scritta in questo modo:
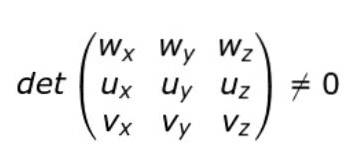
Il prodotto triplo ha un'interpretazione geometrica e rappresenta il volume del parallelepipedo generato dai tre vettori non complanari.
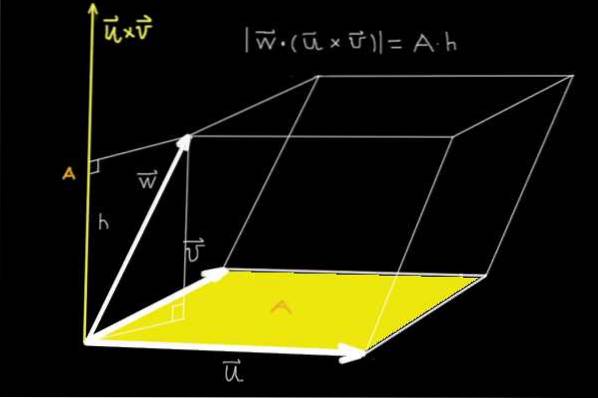
Il motivo è il seguente; Quando due dei vettori non complanari vengono moltiplicati vettorialmente, si ottiene un vettore la cui grandezza è l'area del parallelogramma che generano.
Quindi quando questo vettore viene moltiplicato scalare per il terzo vettore non complanare, ciò che abbiamo è la proiezione su un vettore perpendicolare al piano determinato dai primi due moltiplicati per l'area che determinano..
Cioè, abbiamo l'area del parallelogramma generata dai primi due moltiplicata per l'altezza del terzo vettore.
Condizione alternativa di non complanarità
Se hai tre vettori e nessuno di essi può essere scritto come una combinazione lineare degli altri due, i tre vettori non sono complanari. Sono tre vettori o, v Y w non sono complanari se la condizione:
α o + β v + γ w = 0
È soddisfatto solo quando α = 0, β = 0 e γ = 0.
Esercizi risolti
-Esercizio 1
Ci sono tre vettori
o = (-3, -6, 2); v = (4, 1, 0) e w = (-1, 2, z)
Si noti che il componente z del vettore w È sconosciuto.
Trova l'intervallo di valori che z può assumere in modo tale da garantire che i tre vettori non condividano lo stesso piano.
Soluzione
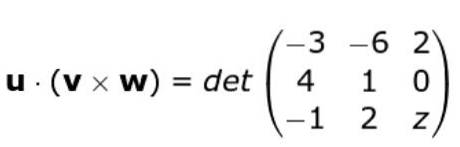
w • ( o X v ) = -3 (z - 0) + 6 (4 z - 0) + 2 (8 + 1) = -3z + 24z + 18 = 21z + 18
Impostiamo questa espressione uguale al valore zero
21 z + 18 = 0
e risolviamo per z
z = -18 / 21 = -6/7
Se la variabile z assumesse il valore -6/7, i tre vettori sarebbero complanari.
Quindi i valori di z che garantiscono che i vettori non siano complanari sono quelli nel seguente intervallo:
z ∈ (-∞, -6 / 7) U (-6/7, ∞)
-Esercizio 2
Trova il volume del parallelepipedo mostrato nella figura seguente:
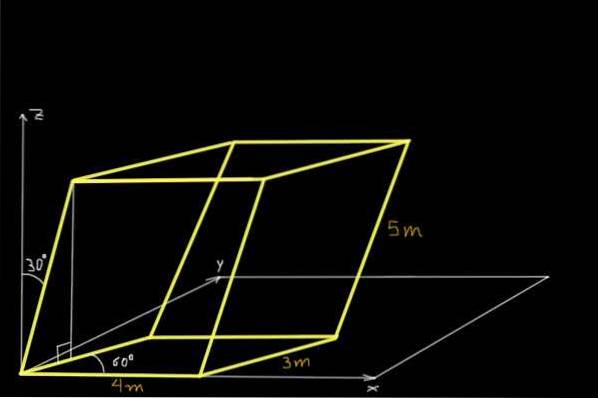
Soluzione
Per trovare il volume del parallelepipedo mostrato in figura, verranno determinate le componenti cartesiane di tre vettori non complanari concorrenti all'origine del sistema di coordinate. Il primo è il vettore o 4m e parallelo all'asse X:
o= (4, 0, 0) m
Il secondo è il vettore v nel piano XY di dimensione 3m formando 60 ° con l'asse X:
v= (3 * cos 60º, 3 * sin 60º, 0) = (1.5, 2.6, 0.0) m
E il terzo il vettore w di 5m e la cui proiezione nel piano XY forma 60º con l'asse X, inoltre w forma 30º con l'asse Z.
w= (5 * sin 30º * cos 60º, 5 * sin 30º * sin 60º, 5 * sin 30º)
Una volta effettuati i calcoli, abbiamo: w= (1,25, 2,17, 2,5) m.
Riferimenti
- Figueroa, D. Series: Physics for Sciences and Engineering. Volume 1. Cinematica. 31-68.
- Fisico. Modulo 8: vettori. Estratto da: frtl.utn.edu.ar
- Hibbeler, R. 2006. Meccanica per ingegneri. Statico. 6a edizione. Continental Publishing Company 28-66.
- McLean, W. Schaum Series. Meccanica per ingegneri: statica e dinamica. 3a edizione. McGraw Hill. 1-15.
- Wikipedia. Vettore. Estratto da: es.wikipedia.org



Nessun utente ha ancora commentato questo articolo.